Вывод рабочей формулы и описание установки. Для выполнения данной лабораторной работы студентам необходимо знать понятия: статистический ансамбль
Для выполнения данной лабораторной работы студентам необходимо знать понятия: статистический ансамбль, вероятность появления результата, функция распределения вероятности, статистические законы Гаусса и Максвелла.
Особое внимание следует обратить на соотношение динамических и статистических закономерностей, на различные примеры их применения и использования. Рассмотреть классические примеры использования динамических закономерностей, расчёт траектории полёта снаряда или самолета, движения планет вокруг Солнца. Обратить внимание, что, зная начальные положения тел и характер сил, действующих на тело во время движения, можно однозначно вычислить положение тела в любые предшествующие и последующие моменты времени.
Рассмотреть затем ряд физических явлений и процессов, в которых результат данного одиночного опыта не может быть предсказан с полной определенностью и носит случайный, вероятностный характер. К таким явлениям относятся, например, распад атомного ядра, испускание электронов нагретой нитью, испускание фотонов атомом, столкновение молекул. Убедиться, что невозможно знать, например, с какой скоростью будет двигаться та или иная молекула, какой энергией она будет обладать, импульсом и т.д. Неопределенность является внутренним свойством, характерной особенностью для тех процессов и явлений, которые определяются коллективным движением или взаимодействием большого числа однотипных объектов.
Усвоить вывод: по отношению к таким явлениям и системам можно поставить лишь один вопрос: какова вероятность того, что интересующая нас физическая величина будет иметь то или иное значение?
Обратить внимание на то место теории, в котором обосновываются понятия вероятности и функции распределения плотности вероятности.
Вероятность понимать как предел, к которому стремится относительная частота появления некоторого события при бесконечно большом числе повторений опыта. Если при 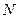 опытах
опытах 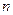 раз получен определенный результат, то вероятность этого результата
раз получен определенный результат, то вероятность этого результата 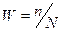 . Вероятность
. Вероятность 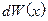 того, что случайная величина
того, что случайная величина  может принимать значения от
может принимать значения от  до
до 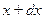 (т.е. находится в интервале значений), является функцией самой этой величины
(т.е. находится в интервале значений), является функцией самой этой величины 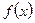 и пропорциональна ширине интервала значений
и пропорциональна ширине интервала значений 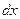 , т.е.
, т.е. 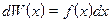 . Запомнить: функция
. Запомнить: функция 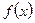 называется функцией распределения вероятности, она показывает, как распределяется вероятность, приходящаяся на один и тот же интервал значений
называется функцией распределения вероятности, она показывает, как распределяется вероятность, приходящаяся на один и тот же интервал значений 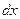 , в зависимости от значений самой величины
, в зависимости от значений самой величины  . Функцию
. Функцию 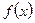 называют функцией распределения плотности вероятности.
называют функцией распределения плотности вероятности.
В лабораторной работе ставится задача: на примере механических моделей, имитирующих беспорядочность и хаотичность движений и столкновений молекул, экспериментально установить вид функций распределения для конкретных физических величин и сравнить полученные результаты с выводами теории.
Обратить внимание на постановку задачи. Система состоит из одинаковых частиц. Движение каждой частицы строго обусловлено
различными причинами. Оно подчиняется обычным законам механики, но из-за большого числа столкновений с другими частицами и со стенками сосуда величина и направление скорости частиц за короткий промежуток времени испытывают огромное число изменений и носят вероятностный, случайный характер.
Можно поставить задачу: чему равна относительная доля молекул 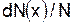 ,
,  - компонента скорости которых (
- компонента скорости которых ( 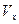 ) лежит в заданном интервале значений от
) лежит в заданном интервале значений от 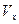 - до
- до 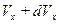 - или какова вероятность
- или какова вероятность 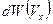 того, что некоторая молекула будет иметь
того, что некоторая молекула будет иметь  -компоненту скорости в интервале между
-компоненту скорости в интервале между 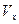 и
и 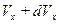 .
.
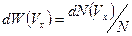 . (1)
. (1)
Из теории следует, что
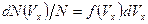 . (2)
. (2)
где 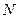 -полное число частиц.
-полное число частиц.
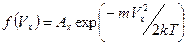 - функция распределения Гаусса.
- функция распределения Гаусса.
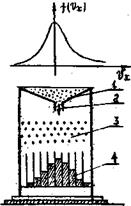
Следует иметь в виду, что функция Гаусса симметрична относительно 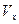 и стремится к нулю при возрастании
и стремится к нулю при возрастании 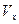 до бесконечности. Графикфункции Гаусса изображен на следующем рисунке.
до бесконечности. Графикфункции Гаусса изображен на следующем рисунке.
|
Постоянная 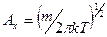 -нормировочный множитель,
-нормировочный множитель,  - масса частицы. Экспериментально закон распределения Гаусса можно проверить с помощью доски Гальтона, эскиз которой изображен на рисунке;
- масса частицы. Экспериментально закон распределения Гаусса можно проверить с помощью доски Гальтона, эскиз которой изображен на рисунке;
1 - воронка с мелкими частицами (дробинки, крупнозернистый песок, пшено);
2 - заслонка;
3 - булавки или гвозди (центры столкновений)
4- ячейки.
Открыв заслонку 2, будем сыпать частицы равномерной струей. При движении каждая частица испытывает многочисленные столкновения с булавками. Это приводит к случайному разбросу компоненты скорости 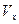 . Вероятность попадания частицы в ту или иную ячейку определится значением компоненты скорости
. Вероятность попадания частицы в ту или иную ячейку определится значением компоненты скорости 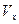 частицы. Чем больше величина
частицы. Чем больше величина 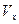 , тем в более далёкую от центра ячейку попадет частица. Число частиц, попавших в ту или иную ячейку, можно трактовать как вероятность того, что компонента скорости
, тем в более далёкую от центра ячейку попадет частица. Число частиц, попавших в ту или иную ячейку, можно трактовать как вероятность того, что компонента скорости 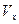 зернышка находится в определенном интервале значений. Так как ширина ячеек одинакова, то высота столбиков частиц в ячейках
зернышка находится в определенном интервале значений. Так как ширина ячеек одинакова, то высота столбиков частиц в ячейках 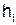 пропорциональна числу зёрен
пропорциональна числу зёрен 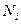 в ячейках, т.е.
в ячейках, т.е. 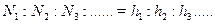 .
.
Дата добавления: 2015-10-06; просмотров: 762;
