Порядок выполнения и обработки данных.
Работа на приборе производится двумя студентами следующим образом. Один студент переворачивает несколько раз прибор (не встряхивать!) и кладёт его на стол. Линейкой замеряют расстояние от одного шарика (обычно находящегося в стороне от остальных), до каждого из остальных (три измерения), после этого замеряют расстояния от второго до третьего и четвёртого шарика (два измерения); и наконец, одно измерение расстояния между третьим и четвёртым шариком. Итого шесть измерений. Опыт повторить 50 раз. Другой студент отмечает каждое названное расстояние в колонках точкой или чёрточкой. Колонки представляют собой интервалы расстояний 1-1,5; 1,5-2; 2- 2,5;…14-14,5; 14,5-15;
15-15,5см.
Дальнейшие измерения теряют смысл из-за конечности диаметра прибора. После окончания наблюдений подсчитывают количество измеренных расстояний в каждом интервале 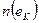 . Относительные частоты попадания отсчетов в те или другие интервалы, полученные путём деления
. Относительные частоты попадания отсчетов в те или другие интервалы, полученные путём деления 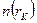 на среднее число попаданий в интервал
на среднее число попаданий в интервал  , дадут радиальную функцию распределения
, дадут радиальную функцию распределения 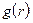
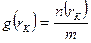 .
.
В нашем случае 50 опытов и 300 измерений 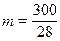 , где знаменатель – число интервалов (колонок).
, где знаменатель – число интервалов (колонок).
Находим среднюю плотность
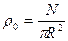 , где
, где 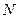 - общее число шаров,
- общее число шаров, 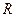 - радиус полости прибора.
- радиус полости прибора.
Вычислим функцию 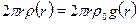 и отложим её значения на графике. В точках с абсциссами посредине интервалов: 1,25; 1,75; 2,25;…14,25; 14,75; 15,25.
и отложим её значения на графике. В точках с абсциссами посредине интервалов: 1,25; 1,75; 2,25;…14,25; 14,75; 15,25.
На полученной кривой выделим первые тени. Найдём
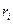 - радиусы координационных слоёв и
- радиусы координационных слоёв и 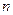 - площадь первого координационного слоя (число ближайших «соседей»).
- площадь первого координационного слоя (число ближайших «соседей»).
Контрольные вопросы.
1. Что такое «ближний» и «дальний» порядок в расположении атомов?
2. Что такое координационное число, координационная сфера?
3. Вероятность стройного события.
4. Функция распределения вероятности.
5. Наивероятнейшее расстояние до данного атома и его место на графике 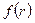 .
.
6. Физический смысл площади прямоугольника, ограниченного графиком 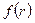 и отрезком
и отрезком  .
.
7. Радиальная функция распределения, её физический смысл.
8. Как определяется число ближайших соседей по графику 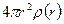 ?
?
9. Как определяется радиус координационной сферы по графику 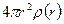 ?
?
Дата добавления: 2015-10-06; просмотров: 646;
