Вывод рабочей формулы и описание установки. При подготовке к лабораторной работе необходимо использовать
При подготовке к лабораторной работе необходимо использовать
методические указания к лабораторной работе "Определение
 коэффициента вязкости методом Стокса". Ограничимся выводом рабочей формулы. Рассмотрим ламинарное течение вязкой жидкости по трубке радиусом
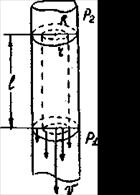
коэффициента вязкости методом Стокса". Ограничимся выводом рабочей формулы. Рассмотрим ламинарное течение вязкой жидкости по трубке радиусом 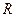 . Благодаря наличию внутреннего трения, скорость течения жидкости наибольшая в центре трубы (рисунок). У стенок, вследствие прилипания молекул жидкости к поверхности, скорость течения равна нулю. Пусть жидкость течёт сверху вниз под влиянием разности давлений
. Благодаря наличию внутреннего трения, скорость течения жидкости наибольшая в центре трубы (рисунок). У стенок, вследствие прилипания молекул жидкости к поверхности, скорость течения равна нулю. Пусть жидкость течёт сверху вниз под влиянием разности давлений 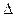 P=P2-P1. В лабораторной работе
P=P2-P1. В лабораторной работе 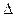 P создаётся гидростатическим давлением столба жидкости. Из теории известно, что скорость течения жидкости на расстоянии
P создаётся гидростатическим давлением столба жидкости. Из теории известно, что скорость течения жидкости на расстоянии 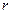 от оси трубки определяется по формуле
от оси трубки определяется по формуле
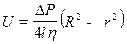 , (1)
, (1)
где  - длина трубки,
- длина трубки,  - коэффициент динамической вязкости жидкости. Определим объём и массу жидкости, вытекающей из трубки за некоторое время
- коэффициент динамической вязкости жидкости. Определим объём и массу жидкости, вытекающей из трубки за некоторое время  . Объём цилиндра радиусом
. Объём цилиндра радиусом 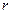 и длиной, образующей
и длиной, образующей  (на рисунке он показан пунктиром), равен
(на рисунке он показан пунктиром), равен  , так как
, так как 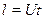 ,
, 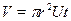 . Продифференцировав это выражение, получим объём жидкости, вытекающей из цилиндрического слоя радиусом
. Продифференцировав это выражение, получим объём жидкости, вытекающей из цилиндрического слоя радиусом 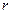 и толщиной
и толщиной  за, время
за, время 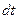
 .
.
Подставляя в место  формулу (1), получим
формулу (1), получим
 .
.
Интегрируя это выражение в пределах от 0 до 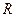 , получим объём жидкости, вытекающей через поперечное сечение трубки
, получим объём жидкости, вытекающей через поперечное сечение трубки
 . (2)
. (2)
Определим массу жидкости  , вытекающей из трубки за единицу времени. Масса жидкости, вытекающей за время
, вытекающей из трубки за единицу времени. Масса жидкости, вытекающей за время  , равна
, равна
 ,
,
где  - плотность жидкости. Тогда
- плотность жидкости. Тогда
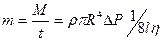 . (3)
. (3)
формула (3) называется формулой Пуазейля. Вискозиметр, используемый в лабораторной работе, изображён на рисунке: 1 – сосуд с исследуемой жидкостью, 2 – узкая длинная трубка, закреплённая на линейке, 3 – резиновая груша, используемая для заполнения трубки жидкостью, 4 – кран, соединяющий верхний конец трубки с атмосферой.
| K:s/ telif |
Заполнить трубку 2 исследуемой жидкостью. Открыть кран 4. Жидкость

|
будет истекать вниз под действием разности
давлений 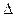 P, создаваемой гидростатическим
P, создаваемой гидростатическим
давлением столба жидкости
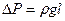 . (4)
. (4)
Измерим время  , за которое уровень жидкости понизился на величину
, за которое уровень жидкости понизился на величину  . Определим скорость истечения
. Определим скорость истечения  и массу жидкости
и массу жидкости  , вытекшей за это
, вытекшей за это
время  ,
,  .
.
Найдем массу жидкости  , вытекшую за единицу времени
, вытекшую за единицу времени
 . (5)
. (5)
Эта же величина определяется формулой Пуазейля. Приравняем правые части формул (3) и (5) и учтём формулу (4), получим окончательную рабочую формулу
 . (6)
. (6)
Из механики жидкостей известно, что переход от ламинарного течения к вихревому (турбулентному), для которого формула Пуазейля (6) не выполняется, происходит при определенных условиях. Эти условия зависят от коэффициента вязкости жидкости  , радиуса трубки
, радиуса трубки 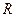 и скорости движения жидкости
и скорости движения жидкости  .
.
При движении жидкости в цилиндрической трубке переход к
турбулентному движению происходит, когда безразмерная величина 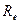 становится больше некоторого критического значения порядка 103
становится больше некоторого критического значения порядка 103


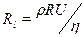 . (7)
. (7)
Величина 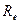 называется числом Рейнольдса (отсюда и обозначение
называется числом Рейнольдса (отсюда и обозначение 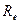 ) Если
) Если 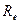 <103 - движение ламинарное, если
<103 - движение ламинарное, если 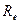 > 103 - турбулентное.
> 103 - турбулентное.
Дата добавления: 2015-10-06; просмотров: 952;
