Вывод рабочей формулы и описание установки. При подготовке к лабораторной работе изучить тему "Явления переносе в жидкостях и газах"

При подготовке к лабораторной работе изучить тему "Явления переносе в жидкостях и газах". Обратить внимание на важную роль, которую играют столкновения между молекулами в явлениях диффузии, вязкости, теплопроводности, а также на общность молекулярного механизма явлений переноса. Следует усвоить следующие теоретические понятия: средняя длина свободного пробега молекул, поток некоторой величины - количество этой величины, проходящее в единицу времени через единицу площади поверхности, градиент скалярной функции.

Необходимо чётко представлять, что механизм возникновения внутреннего трения между слоями жидкости, движущимися с различными скоростями, заключается в том, что вследствие хаотического (теплового) движения происходит обмен молекулами между слоями, в результате чего импульс слоя, движущегося быстрее, уменьшается, а движущегося медленнее - увеличивается, что приводит к торможению слоя, движущегося быстрее, т.е. к возникновению силы внутреннего трения. Исходя из механизма явления, следует понимать коэффициент внутреннего трения или коэффициент динамической вязкости как физическую величину, численно равную силе внутреннего трения, действующей между слоями площадью соприкосновения, равной единице, при градиенте скорости в направлении, перпендикулярном поверхности слоев, равном единице.

Прибор Стокса (рисунок) представляет собой стеклянный цилиндр I с налитой в него исследуемой жидкостью. В лабораторной работе

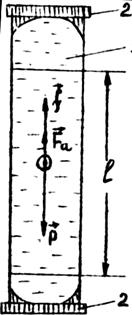используется либо глицерин, либо касторовое масло. Название исследуемой жидкости и её плотность указаны на установке. Внутри сосуда находятся стальные шарики различного диаметра. Диаметры шариков указаны на установке. Цилиндр с обоих концов закрыт пробками 2, имеющими изнутри форму воронок. При переворачивании цилиндра вокруг горизонтальной оси воронки обеспечивают движение шариков вдоль осевой линии сосуда.

Для получения рабочей формулы необходимо рассмотреть движение шарика в вязкой жидкости. Учесть, что при малых скоростях движения позади шарика завихрений не возникает. Слой жидкости, непосредственно соприкасающийся с шариком, прилипает к его поверхности и полностью им увлекается. Следующий слой жидкости увлекается за шариком с меньшей скоростью. Слои жидкости как бы скользят относительно друг друга. Между слоями возникает сила внутреннего трения, а на шарик действует сила сопротивления, тормозящая его движение. Нужно уяснить, что сила сопротивления, действующая на шарик, как раз и обусловлена вязкостью жидкости. Воспользоваться далее выводом теории.

Для шариков, движущихся в неограниченном объеме вязкой жидкости по закону Стокса, сила сопротивления равна

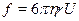, (1)

где - радиус шарика, - скорость его движения; - коэффициент динамической вязкости жидкости.

Нужно учесть, что если шарик свободно падает в жидкости, то кроме силы 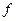на него будут действовать сила тяжести 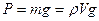и выталкивающая (архимедова) сила 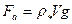( 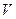- объём шарика, 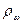- плотность материала шарика, 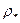- плотность жидкости). Шарик лишь в самый начальный момент будет падать ускоренно; по мере возрастания скорости падения возрастает сила трения 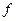. При некоторой скорости падения силы 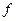и 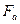, уравновесят силу тяжести 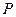. С этого момента шарик будет падать с постоянной скоростью. Эту скорость найти из условия 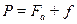. После подстановки получить 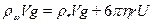, Решить это уравнение относительно скорости и убедиться, что 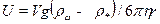(2),

где 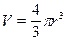- объём шарика. Получить затем рабочую формулу

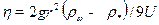. (3)

Нужно помнить, что эта формула получена в предположении, что шарик движется в неограниченной жидкой среде, когда нет краевых эффектов. Однако она даёт достаточно точный результат, если диаметр цилиндра не меньше пяти диаметров шарика. В приборе Стокса это условие соблюдается.

В выражении (3) скорость равномерного движения шарика можно определить, если измерить расстояние между отметками на сосуде и время , за которое шарик проходит это расстояние. Подставить скорость 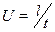в формулу (3) и получить формулу, которую использовать для расчётов

Размерность коэффициента динамической вязкости представить в единицах системы СИ.

В качестве дополнительного исследования рассчитать 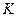- поправочный коэффициент 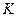, который учитывает влияние стенок и дна цилиндра на характер движения шарика по формуле

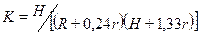, (5)

где 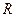- радиус цилиндра; - радиус шарика; - высота столба жидкости в цилиндре.