Вывод рабочей формулы и описание установки. Следует обратить внимание на то, что в данной лабораторной работе для определения малых промежутков времени (10-3) применяется метод конденсаторного

Следует обратить внимание на то, что в данной лабораторной работе для определения малых промежутков времени (10^-3) применяется метод конденсаторного хронометра, основанный на изменении напряжения на конденсаторе в процессе удара шара за время, которое нужно определить.

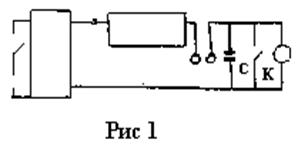
Лабораторная установка для определения времени удара состоит из электрической схемы (рис. I), в которую включены два металлических шара, выполняющие роль ключа, электромагнита для фиксации угла отклонения правого шара и магнита для фиксации левого шара, электростатического вольтметра, кнопки сброса показаний вольтметра, ключа K₁-для включения схемы в сеть, ключа К₂-для включения электромагнита, ключа К₃-для зарядки блока питания.

В схему зарядки конденсатора включен стабилизатор тока, поэтому напряжение на конденсаторе пропорционально времени соприкосновения шаров, т.е. времени соударения 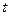. Из определения электроёмкости конденсатора 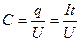-получаем выражение для времени удара шаров 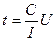.(I) В лабораторной установке два металлических шара одинаковой массы 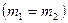подвешены на практически нерастяжимых нитях так, что при ударе центры шаров находятся на одной линии, т.е. происходит центральный удар. Если правый шар 2 отвести от положения равновесия на угол a и отпустить его, то в момент удара он передаёт левому шару I импульс. Согласно закону сохранения импульса

,

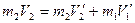где 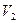- скорость правого шара в момент, предшествующий удару, 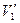и 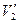– скорости шаров после удара.

Используя закон сохранения энергии, получим для описанного выше удара

.

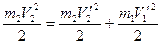Учитывая, что массы шаров одинаковы, уравнения законов сохранения импульса и энергии можно записать в виде 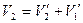, 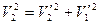откуда .

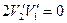Так как под действием удара второй шар начал двигаться, то 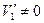,тогда 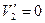. Таким образом, при равенстве масс двух соударяющихся шаров, один из которых неподвижен, движущийся шар полностью передает

импульс неподвижному и останавливается. Поэтому 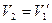, т.е. шары как бы обмениваются скоростями. Если второй шар после удара остаётся в покое, то 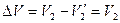и второй закон Ньютона 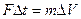можно записать в ви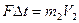де , где 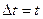- время удара. Следовательно, сила удара 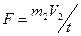. (2)

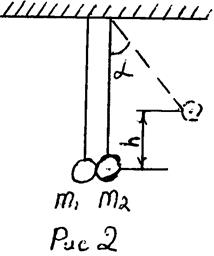
Шар, отведенный от положения равновесия на угол (рис. 2), обладает запасом потенциальной энергии 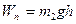. Эта энергия в начальный момент соприкосновения полностью переходит в кинетическую энергию 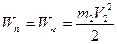.Откуда скорость шара 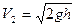. (3)

Из рис. 2 следует 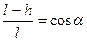, поэтому 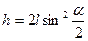. Подставляя полученное выражение для 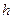в (3), получим рабочую формулу для определения скорости шара

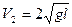
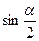. (4)

Следует обратить внимание на то, что выражения (I), (2), (4) - рабочие формулы для вычисления средних значений времени удара, силы удара, скорости шара. Формулы для вычисления абсолютных и относительных погрешностей указанных величин необходимо получить самостоятельно.