Вывод рабочей формулы и описание установки
Прежде чем приступить к работе, необходимо усвоить основные термодинамические понятия и положения: теплота, работа, внутренняя энергия, функция состояния системы, теплоёмкость, первое начало термодинамики и его применение к изопроцессам идеального газа. Следует обратить внимание на вывод и физическое содержание следующих формул: 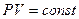 (уравнение изотермического процесса),
(уравнение изотермического процесса), 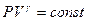 (уравнение адиабатического процесса),
(уравнение адиабатического процесса), 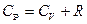 (уравнение Майера),
(уравнение Майера), 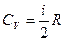 ,
, 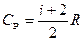 . Следует запомнить данный вывод теории: одна и та же система, в зависимости от происходящего в ней процесса, обладает различными теплоёмкостями. Поэтому теплоёмкость нельзя считать характеристикой только самого вещества.
. Следует запомнить данный вывод теории: одна и та же система, в зависимости от происходящего в ней процесса, обладает различными теплоёмкостями. Поэтому теплоёмкость нельзя считать характеристикой только самого вещества.
Особое внимание следует обратить на то, что при адиабатическом процессе 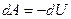 , т.е. газ совершает работу только за счёт изменения внутренней энергии, а знак минус означает, что увеличение объёма газа (расширение) сопровождается понижением его температуры, а сжатие - повышением.
, т.е. газ совершает работу только за счёт изменения внутренней энергии, а знак минус означает, что увеличение объёма газа (расширение) сопровождается понижением его температуры, а сжатие - повышением.
Полезно сравнить изотермический и адиабатический процессы и ответить на следующие вопросы: Почему адиабатический процесс относится к изопроцессам? Почему не графике 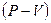 адиабата идёт круче изотермы? Что это означает физически?
адиабата идёт круче изотермы? Что это означает физически?
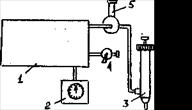
Установка, используемая в лабораторной работе для определения коэффициента Пуассона 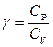 , изображена на рисунке 1:
, изображена на рисунке 1:
1-теплоизолированный баллон с воздухом, 2-манометр, 3-насос, 4-кран,
5-предохранительный клапан.
 Эксперимент следует проводить в такой последовательности. Закрыть кран и накачать в баллон воздух. Качать неторопливо, аккуратно и наблюдать за показаниями манометра. Давление воздуха в сосуде увеличивается по сравнению с атмосферным давлением и через некоторое время станет равным
Эксперимент следует проводить в такой последовательности. Закрыть кран и накачать в баллон воздух. Качать неторопливо, аккуратно и наблюдать за показаниями манометра. Давление воздуха в сосуде увеличивается по сравнению с атмосферным давлением и через некоторое время станет равным 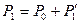 , где
, где 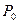 - атмосферное давление,
- атмосферное давление, 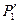 - избыток давления воздуха в баллоне над атмосферным. Примерно через 1-2 мин открыть на короткое время кран. Как только давление в баллоне сравняется с атмосферным (это значит, что
- избыток давления воздуха в баллоне над атмосферным. Примерно через 1-2 мин открыть на короткое время кран. Как только давление в баллоне сравняется с атмосферным (это значит, что 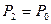 ), закрыть кран.
), закрыть кран.
Пусть 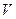 - объём баллона,
- объём баллона, 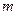 - масса воздуха в баллоне после накачивания. Когда кран был открыт, некоторая масса воздуха
- масса воздуха в баллоне после накачивания. Когда кран был открыт, некоторая масса воздуха 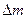 вышла из баллона» В баллоне осталась масса
вышла из баллона» В баллоне осталась масса 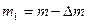 . Нужно учесть, что масса
. Нужно учесть, что масса 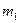 занимает весь объём баллона, а перед открытием крана эта масса занимает меньший объём
занимает весь объём баллона, а перед открытием крана эта масса занимает меньший объём 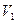 .
.
Следует обратить внимание, что при открытом кране избыток воздуха из баллона выходит достаточно быстро. Процесс выравнивания давления внутри баллона и снаружи кратковременный. За время протекания процесса заметного теплообмена между воздухом и стенками баллона нет. Процесс т.о. можно считать адиабатическим. Для массы воздуха 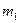 можно написать уравнение Пуассона для начального состояния, характеризующегося давлением
можно написать уравнение Пуассона для начального состояния, характеризующегося давлением 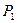 , объёмом
, объёмом 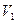 , и конечного с параметрами
, и конечного с параметрами 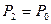 и
и 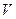 :
: 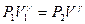 . (I)
. (I)
В дальнейшем процесс будет развиваться так. При адиабатическом расширении (кран открыт) температура воздуха в баллоне понизится. После закрытия крана, в результате теплообмена, температура воздуха в баллоне достаточно быстро повысится и станет равной комнатной. При этом давление газа поднимется до величины 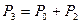 . (2) Процесс на этом закончится.
. (2) Процесс на этом закончится.
Итак, начальное состояние воздуха в баллоне характеризуется
параметрами 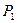 ,
, 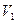 и комнатной температурой
и комнатной температурой 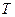 , конечное - параметрами
, конечное - параметрами 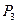 ,
, 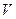 и также комнатной температурой
и также комнатной температурой 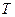 . Так как начальное и конечное состояния наблюдаются при одинаковой температуре, на основании закона Бойля-Мариотта, можно написать
. Так как начальное и конечное состояния наблюдаются при одинаковой температуре, на основании закона Бойля-Мариотта, можно написать 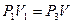 (3). Если решить уравнения (I) и (3), можно получить
(3). Если решить уравнения (I) и (3), можно получить
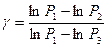 . (4)
. (4)
Разложить 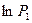 и
и 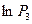 в ряд Тейлора и ограничиться первыми двумячленами ряда:
в ряд Тейлора и ограничиться первыми двумячленами ряда:
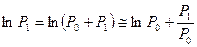 ;
; 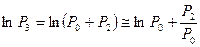 .
.
Подставить эти выражения в формулу (4) и получить рабочую формулу
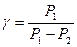 . (5)
. (5)
Порядок выполнения работы
1. Закрыть кран и накачать насосом немного воздуха в баллон. Выждав 2-3 мин, пока температура воздуха в баллоне не станет равной комнатной, измерить избыточное давление 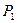 .
.
2. Энергичным движением открыть кран. Когда стрелка манометра достигнет нуля, кран быстро закрыть. При адиабатическом расширении воздух в баллоне охлаждается. Необходимо выждать 2-3 мин, пока воздух в баллоне нагреется до комнатной температуры. Измерить избыточное давление 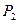 .
.
3.Опыт повторить 5 раз, создавая одно и то же начальное избыточное
давление 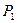 ,. Погрешности
,. Погрешности 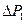 и
и 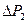 вычислить как погрешности прямых измерений. Относительную погрешность
вычислить как погрешности прямых измерений. Относительную погрешность 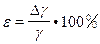 вычислить по методу расчёта погрешностей для косвенных измерений. Результаты измерений и вычислений записать в следующую таблицу:
вычислить по методу расчёта погрешностей для косвенных измерений. Результаты измерений и вычислений записать в следующую таблицу:
| № Опыта | Р1, Па | 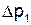 , Па , Па
| Р2, Па | 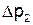 , Па , Па
| 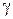
| 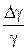
| 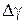
| 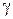 теор теор
| |
| Ср. зн. |
4. Рассчитать теоретическое значение 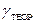 для воздуха, считая его двухатомным газом.
для воздуха, считая его двухатомным газом.
5. Пользуясь формулой 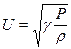 , где
, где  - скорость звука в воздухе,
- скорость звука в воздухе, 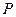 - давление,
- давление,  - плотность, рассчитать
- плотность, рассчитать  . Сравнить с литературными данными (
. Сравнить с литературными данными ( 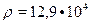 г/см3).
г/см3).
Вопросы для самоконтроля
1. . Какой процесс называется адиабатическим? Получите уравнение адиабаты в координатах  ,
, 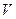 .
.
2. . Почему  и
и 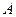 не являются функциями состояния термодинамической системы?
не являются функциями состояния термодинамической системы?
3. Почему 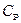 больше
больше 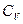 ? Получите уравнение
? Получите уравнение 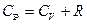 .
.
4. Как изменяется температура газа при адиабатическом процессе? Почему адиабатический процесс относится к изопроцессам идеального газа?
5. От чего зависит точность определения 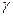 в данной работе?
в данной работе?
Дата добавления: 2015-10-06; просмотров: 1779;
