Метод Гаусса

Одним з найпоширеніших методів розв'язування систем лінійних рівнянь є метод послідовного виключення невідомих, або метод Гаусса. Цей метод запропонований К. Гауссом і ґрунтується на елементарних перетвореннях системи рівнянь

Метод Гаусса розв’язування системи лінійних алгебраїчних рівнянь полягає в послідовному виключенні змінних і перетворенні системи рівнянь

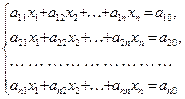(1.6)

до трикутного вигляду

(1.7)

Припустимо, що в системі (6) коефіцієнт 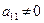. Якщо ця умова не виконується, то на перше місце переносимо таке рівняння, щоб виконувалась умова .

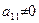За допомогою першого рівняння виключимо х₁ із решти рівнянь. Обчислення виконаємо в таблиці:

Іноді вводять контрольний стовпець 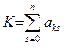, що дає змогу виявляти помилки.

Поділивши перший рядок на а₁₁, позначимо

.

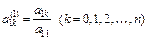Далі перший рядок множимо послідовно на а₂₁ і віднімаємо від другого рядка, множимо на а₃₁ і віднімаємо від третього рядка і т. д.

Позначивши

,

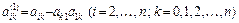дістанемо таблицю коефіцієнтів:

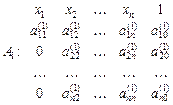
Для невідомих 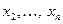маємо систему 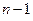рівнянь. Міркуючи, як і раніше, виключимо х₂ з усіх рівнянь, починаючи з третього. Для цього спочатку поділимо другий рядок на 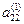. Якщо коефіцієнт , то переставимо рівняння так, щоб виконувалася умова .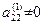

Позначивши

,

помножимо другий рядок послідовно на 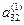і віднімемо від третього рядка; на 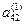і віднімемо від четвертого рядка і т.д. Дістанемо таблицю коефіцієнтів:

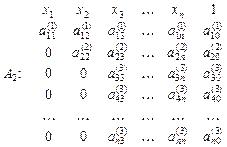
Продовжуючи процес виключення невідомих, дістаємо нарешті таблицю:

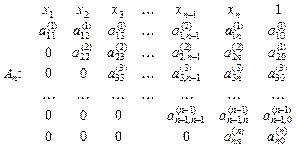
Таблиця коефіцієнтів при невідомих набирає трикутного вигляду. На головній діагоналі всі елементи 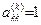. Запишемо відповідну систему рівнянь:

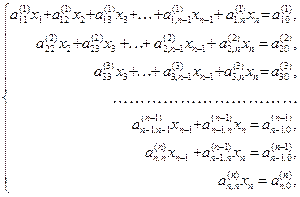(1.8)

Цю систему розв’язують, починаючи з останнього рівняння. Спочатку знаходять 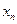і підставляють в передостаннє рівняння, з якого визначають 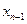, і т.д.

Якщо система рівнянь з n невідомими має єдиний розв’язок, то ця система завжди може бути перетворена до трикутного вигляду.

У загальному випадку метод Гаусса застосовується для дослідження та розв’язування системи рівнянь з n невідомими

(1.9)

Утворимо таблицю коефіцієнтів:

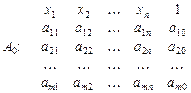
Скориставшись методом виключення Гаусса і переставивши перші n стовпців, перетворимо таблицю до такого вигляду:

.

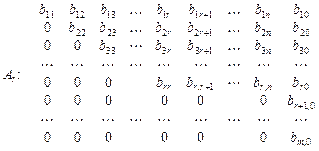
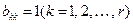Якщо хоча б один із коефіцієнтів відмінний від нуля, то система рівнянь (9) несумісна і не має розв’язків. Якщо всі коефіцієнти 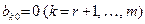, то система рівнянь (9) сумісна. У такому разі маємо r базисних невідомих, що відповідають першим r стовпцям, решта 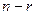невідомих є вільними.