Приклади

Розв’язати систему рівнянь методом Гаусса:

а)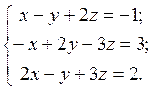

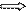а) Виконуємо елементарні перетворення над рядками розширеної матриці даної системи (позначатимемо це символом )

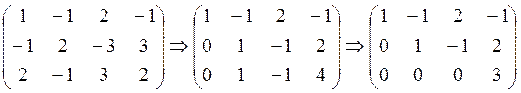
Таким чином, система а) еквівалентна системі

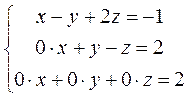
в останньому рівнянні вільний член дорівнює двом, а коефіцієнт при невідомих дорівнюють нулю (тобто 0 = 2­), тому система несумісна.

б) 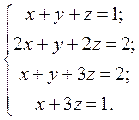Маємо

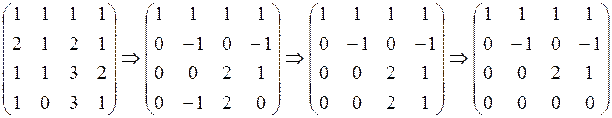
Отже система б) еквівалентна системі трикутного вигляду

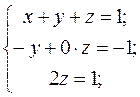і має єдиний розв’язок :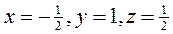

в) 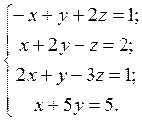Маємо

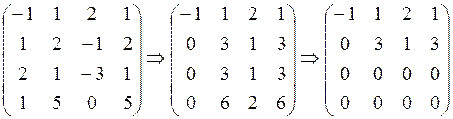
Отже система в) еквівалентна системі трапецієподібного вигляду

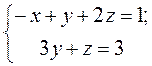
і має безліч розв’язків. З останньої системи знаходимо

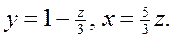
Таким чином розв’язки системи в) мають такий вигляд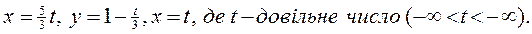

Зазначимо, що жодну з наведених у цьому прикладі систем не можна розв’язувати ні за формулами Крамера, ні матричним способом.