Матричний метод

ПЛАН

1. Матричний метод розв’язання систем лінійних алгебраїчних рівнянь

2. Метод Крамера розв’язання систем лінійних алгебраїчних рівнянь

3. Метод Гауса розв’язання систем лінійних алгебраїчних рівнянь

Матричний метод

Повернемось до системи рівнянь

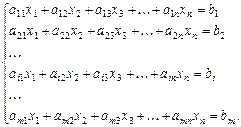(1.1)

і утворимо матриці: А — з коефіцієнтів при невідомих, Х — з невідомих, В — з вільних членів:

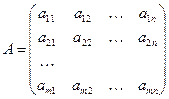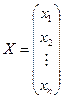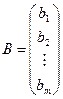, , . (1.2)

Тоді згідно з означенням добутку матриць систему рівнянь (1.1) можна записати в матричному вигляді: 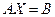, (1.3)

який значно скорочує запис системи рівнянь.

Припустимо, що система складається з n лінійних рівнянь з n невідомими, матриця А — квадратна і 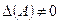— матриця невироджена. Тоді для матриці А побудуємо обернену А^–1 — вона за тих припущень, які щойно зроблено, існує. Помноживши тепер матричну рівність АХ = В зліва на матрицю А^–1, дістанемо:

,

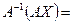
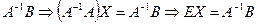або остаточно .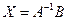

Останній вираз — це розв’язок системи лінійних рівнянь. Зауважимо, що в такому вигляді можна записати розв’язок будь-якого матричного рівняння, якщо матриця А задовольняє умови існування А^–1.