Извлечение корней из комплексных чисел.

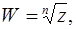Корнем n-ой степени из комплексного числа z называется такое комплексное число W, n-ая степень которого

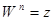
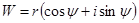даст z, т.е. если и то или

У двух равных комплексных чисел модули равны, а разность аргументов кратна 2p. Поэтому r = r ⁿ,

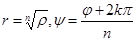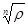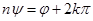(k = 0,±1, ±2, …), откуда ( - арифметическое значение корня).

Итак (4)

Давая k значения k = 0, 1, 2, …, n-1 в (4) получим n разных значений W₀, W₁, …, W_n-1 корня. Очевидно, для

k^¢ = k ± mn получим

Геометрически комплексные числа W₀, W₁, …,W_n-1 находятся на окружности с центром в начале О, они совпадают с вершинами правильного n – угольника, вписанного в эту окружность.

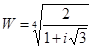Пример. Вычислить и дать геометрическую интерпретацию.

Решение. Представим число в тригонометрической форме.

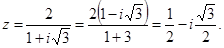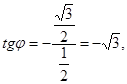Тогда откуда

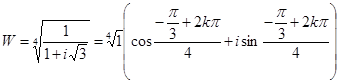Следовательно (k = 0,1,2,3).

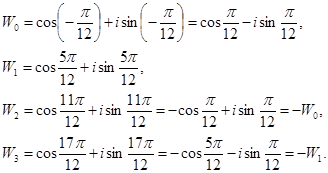Имеем

Геометрическое изображение значений корня на рис. 2.

Рис. 2

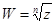Пример. Вычислить и дать геометрическую интерпретацию

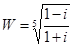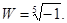a) ; b)

Сделаем два замечания.

1. Мы уже видели, что комплексное число z = x + iy может быть представлено на плоскости XOY (её в этом случае называют комплексной плоскостью) либо точкой M(x,y) или радиус – вектором этой точки. Тогда геометрический смысл операций сложения и вычитания комплексных чисел хорошо виден из чертежа (рис.3): сумма и разность комплексных чисел z₁ и z₂ представляются векторами – ориентированными диагоналями параллелограмма, построенного на векторах z₁ и z₂.

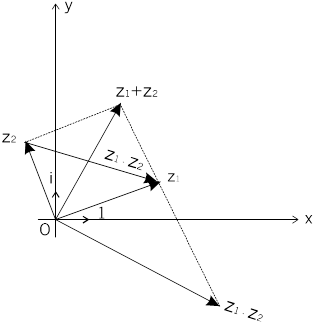
Рис. 3

2. «Мнимые» числа, как квадратные корни из отрицательных чисел, были впервые рассмотрены в XVI веке (Г. Кардан). До середины XVIII века комплексные числа лишь эпизодически появлялись в работах некоторых математиков (И. Ньютона, Н. Бернулли, А. Клеро). Первое изложение теории комплексных чисел на русском языке принадлежит Л. Эйлеру («Алгебра», Петербург, 1963 г.); Символ «i» был введен Эйлером. Геометрическая интерпретация комплексных чисел восходит к концу XVIII века (Г. Вессель).