Определение комплексного числа. Алгебраические операции в множестве комплексных чисел.

Комплексные числа.

Комплексным числом называют всякую упорядоченную пару (а, b) действительных чисел. Его обозначают z = (a, b). Действительные числа а и b называют соответственно действительной и мнимой частью комплексного числа z:

a = Re z и b = Jm z

Пусть имеются два комплексных числа z₁ = (a₁, b₁) и z₂ = (a₂, b₂). Они называются равными тогда и только тогда, когда a₁ = a₂ и b₁ = b₂.

Суммой (разностью) двух комплексных чисел z₁ и z₂ называют комплексное число z = z₁ ± z₂, действительная часть которого есть a₁ + a₂ (a₁ – a₂), а мнимая b₁ + b₂ (b₁ – b₂): z = z₁ ± z₂ = (a₁ ± a₂, b₁ ± b₂).

Произведением чисел z₁ и z₂ называется комплексное число z₁z₂ = (a₁a₂ – b₁b₂, a₂b₁ + a₁b₂).

Если z₂ ¹ 0 (т.е. a₂ ¹ 0, b₂ ¹ 0) частным (отношением) двух комплексных чисел называют комплексное число:

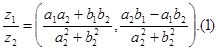Действительные числа являются частным случаем комплексных чисел, они есть числа вида: z = (a, 0) = a. Комплексные числа вида z = (0, b) называют чисто мнимыми (или просто мнимыми). В множестве комплексных чисел мнимое число (0б 1) играет особо важную роль, его обозначают

i =(0, 1).

Найдем i² = (0, 1)(0, 1) = (-1, 0) = -1, т.е. i² = -1. С помощью числа i комплексное число z = (a, b) может быть записано в таком виде:

z = (a, b) = (a, 0) + (0, b) = (a, 0) + (b, 0)(0, 1) = a + bi. (2)

Это выражение (2) называют алгебраической формой комплексного числа z = (a, b). Число a – ib,

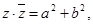
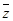обозначаемое как , называют сопряжённым комплексному числу z. Очевидно т.е. произведение сопряжённых комплексных чисел есть неотрицательное действительное число. Очевидны следующие свойства сложения и умножения комплексных чисел:

a) Коммутативность: z₁ + z₂ = z₂ + z₁; z₁z₂ = z₂z₁;

b) Ассоциативность: z₁ + (z₂ + z₃) = (z₁ + z₂) + z₃; z₁(z₂z₃) = (z₁z₂)z₃;

c) Дистрибутивность (умножения по отношению к сложению): (z₁ + z₂)z₃ = z₁z₃ + z₂z₃.

Заметим, что отношение комплексных чисел (1) можно получить (так это и делают на практике) умножением

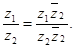
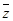на ₂ числителя и знаменателя:

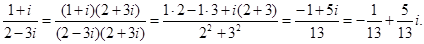Пример.