Тема 28: Эмпирическая функция распределения вероятностей

1. Из генеральной совокупности 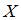извлечена выборка объема :
,
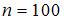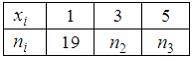эмпирическая функция распределения вероятностей которой имеет вид:

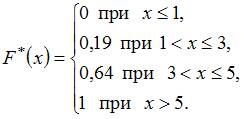
Тогда …

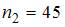
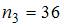
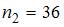
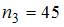
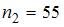
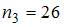
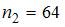
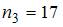
Решение:
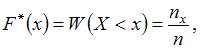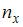По определению где – число вариант, меньших 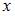. Тогда при 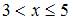, 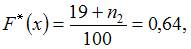то есть 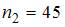, а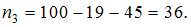

2. Из генеральной совокупности 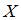извлечена выборка объема :
.
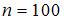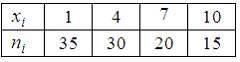Тогда ее эмпирическая функция распределения вероятностей 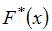имеет вид …

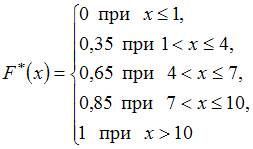
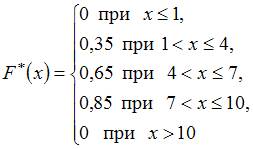
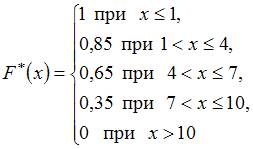
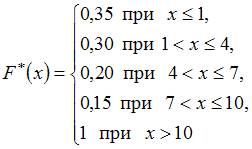
Решение:
По определению 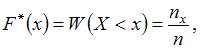где 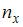– число вариант, меньших 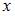. Тогда
а) при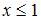
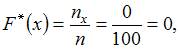
б) при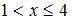
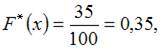
в) при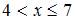
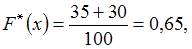
г) при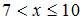
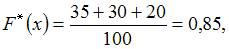
д) при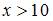
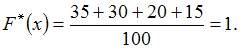
Следовательно,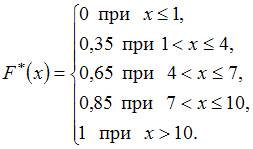

3. Из генеральной совокупности 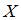извлечена выборка объема :
.
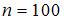Тогда ее эмпирическая функция распределения вероятностей 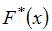имеет вид …

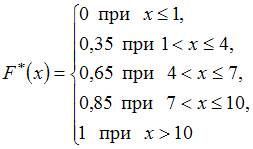
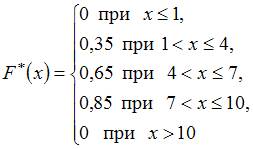
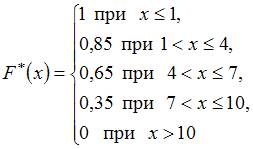
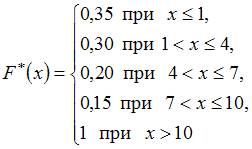
Решение:
По определению 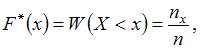где 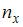– число вариант, меньших 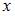. Тогда
а) при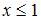
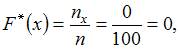
б) при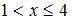
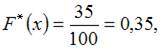
в) при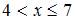
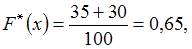
г) при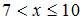
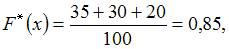
д) при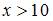
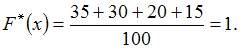
Следовательно,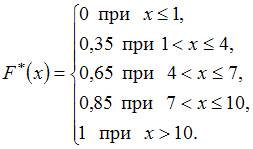

5.Из генеральной совокупности 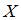извлечена выборка объема :
,
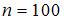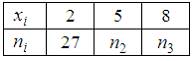эмпирическая функция распределения вероятностей которой имеет вид:

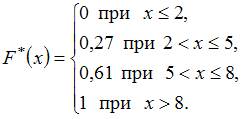
Тогда …

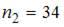
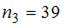
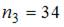
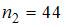
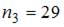
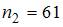
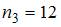
Решение:
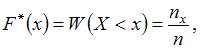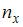По определению где – число вариант, меньших 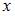. Тогда при 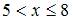, 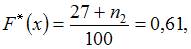то есть 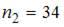, а .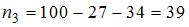

Тема 29: Основные понятия об оценках параметров распределения

1. Дан доверительный интервал 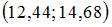для оценки математического ожидания нормально распределенного количественного признака. Тогда точность этой оценки равна …

1,12

0,01

2,24

13,56

Решение:
Точность интервальной оценки 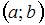определяется как 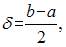то есть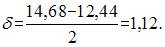

3. Дан доверительный интервал 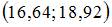для оценки математического ожидания нормально распределенного количественного признака. Тогда при увеличении объема выборки этот доверительный интервал может принять вид …

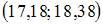
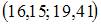
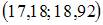
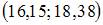
Решение:
Доверительный интервал для оценки математического ожидания нормально распределенного количественного признака можно представить в виде симметричного интервала 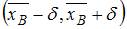, где точечная оценка математического ожидания 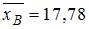, а точность оценки 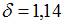. В случае увеличения объема выборки точность оценки улучшается, то есть значение 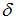будет меньше 1,14.

4. Дан доверительный интервал 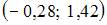для оценки математического ожидания нормально распределенного количественного признака. Тогда при уменьшении надежности (доверительной вероятности) оценки доверительный интервал может принять вид …

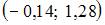
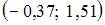
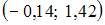
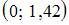
Решение:
Доверительный интервал для оценки математического ожидания нормально распределенного количественного признака можно представить в виде симметричного интервала 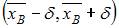, где точечная оценка математического ожидания 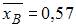, а точность оценки 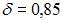. В случае уменьшения надежности точность оценки улучшается, то есть значение 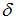будет меньше 0,85.