Тема 24: Интегральная формула Лапласа
1. Вероятность появления некоторого события в каждом из 400 независимых испытаний постоянна и равна 0,8. Тогда вероятность того, что событие появится не менее 300 и не более 328 раз, следует вычислять как …
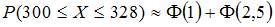 , где
, где 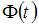 – функция Лапласа
– функция Лапласа
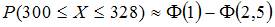 , где
, где 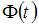 – функция Лапласа
– функция Лапласа
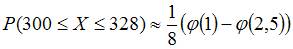 , где
, где 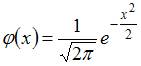
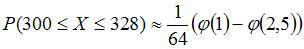 , где
, где 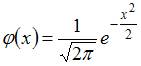
Решение:
Для биномиального распределения вероятностей существует предельное (при 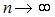 ) распределение, и это распределение является асимптотически нормальным. Это означает, что при больших значениях числа испытаний
) распределение, и это распределение является асимптотически нормальным. Это означает, что при больших значениях числа испытаний 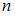 расчет по формуле Бернулли
расчет по формуле Бернулли 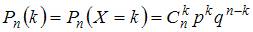 становится практически невозможным, особенно когда надо вычислять вероятности не отдельного равенства (события)
становится практически невозможным, особенно когда надо вычислять вероятности не отдельного равенства (события) 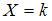 , а неравенств вида
, а неравенств вида 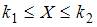 . Для вычисления таких вероятностей на практике используется интегральная формула Лапласа
. Для вычисления таких вероятностей на практике используется интегральная формула Лапласа 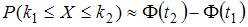 , где
, где 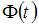 – функция Лапласа, а
– функция Лапласа, а 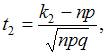
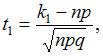
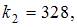
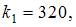
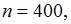
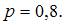
Следовательно,
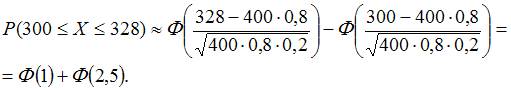
2. Вероятность появления некоторого события в каждом из 100 независимых испытаний постоянна и равна 0,2. Тогда вероятность того, что событие появится не менее 18 и не более 24 раз, следует вычислять как …
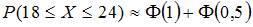 , где
, где 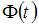 – функция Лапласа
– функция Лапласа
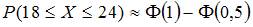 , где
, где 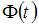 – функция Лапласа
– функция Лапласа
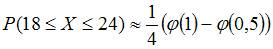 , где
, где 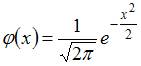
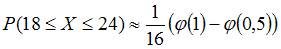 , где
, где 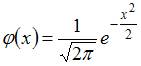
Решение:
Для биномиального распределения вероятностей существует предельное (при 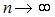 ) распределение, и это распределение является асимптотически нормальным. Это означает, что при больших значениях числа испытаний
) распределение, и это распределение является асимптотически нормальным. Это означает, что при больших значениях числа испытаний 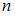 расчет по формуле Бернулли
расчет по формуле Бернулли 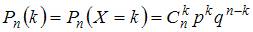 становится практически невозможным, особенно когда надо вычислять вероятности не отдельного равенства (события)
становится практически невозможным, особенно когда надо вычислять вероятности не отдельного равенства (события) 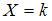 , а неравенств вида
, а неравенств вида 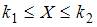 . Для вычисления таких вероятностей на практике используется интегральная формула Лапласа
. Для вычисления таких вероятностей на практике используется интегральная формула Лапласа 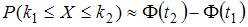 , где
, где 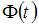 – функция Лапласа, а
– функция Лапласа, а 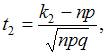
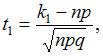
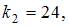
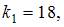
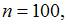
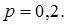
Следовательно,
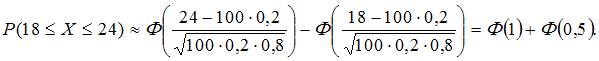
3. Вероятность того, что деталь не пройдет проверку ОТК, равна 0,15. Тогда вероятность того, что среди 300 случайно отобранных деталей окажется не менее 50 деталей, не прошедших проверку ОТК, следует вычислить по …
интегральной формуле Лапласа
формуле полной вероятности
формуле Пуассона
локальной формуле Лапласа
Решение:
Для биномиального распределения вероятностей существует предельное (при 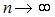 ) распределение, и это распределение является асимптотически нормальным. Это означает, что при больших значениях числа испытаний
) распределение, и это распределение является асимптотически нормальным. Это означает, что при больших значениях числа испытаний 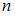 расчет по формуле Бернулли
расчет по формуле Бернулли 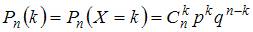 становится практически невозможным, особенно когда надо вычислять вероятности не отдельного равенства (события)
становится практически невозможным, особенно когда надо вычислять вероятности не отдельного равенства (события) 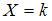 , а неравенств вида
, а неравенств вида 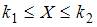 . Для вычисления таких вероятностей на практике используется интегральная формула Лапласа
. Для вычисления таких вероятностей на практике используется интегральная формула Лапласа 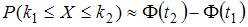 , где
, где 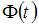 – функция Лапласа, а
– функция Лапласа, а 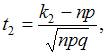
Дата добавления: 2015-09-29; просмотров: 2765;
