Функция Лапласа
Найдем вероятность попадания случайной величины, распределенной по нормальному закону, в заданный интервал:
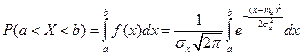 .
.
Обозначим: 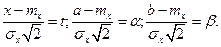
Тогда: 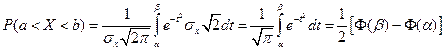 .
.
Интеграл  не выражается через элементарные функции. Введём в рассмотрение функцию:
не выражается через элементарные функции. Введём в рассмотрение функцию:
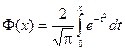 ,
,
которая называется функцией Лапласаили интегралом вероятностей.
Значения этой функции при различных значениях х посчитаны и приводятся в специальных таблицах. График функции Лапласа имеет вид
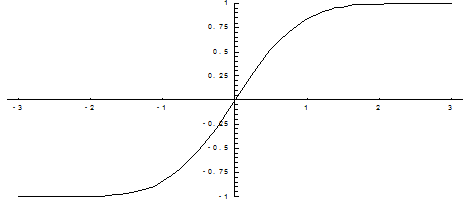
Функция Лапласа обладает следующими свойствами:
1) 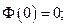 2)
2) 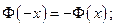 3)
3) 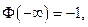
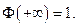
Функцию Лапласа также называют функцией ошибок.
Нормированнаяфункция Лапласа связана с функцией Лапласа соотношением:

График нормированной функции Лапласа имеет вид:
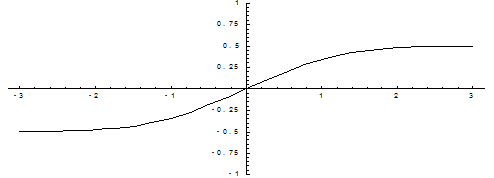
При рассмотрении нормального закона распределения выделяется важный частный случай, известный как правило трех сигм.
Запишем вероятность того, что отклонение нормально распределенной случайной величины от математического ожидания меньше заданной величины D:
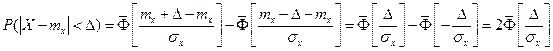 .
.
Если принять D 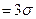 , то получаем с использованием таблиц значений функции Лапласа:
, то получаем с использованием таблиц значений функции Лапласа:

т.е. вероятность того, что случайная величина отклонится от своего математического ожидание на величину, большую чем утроенное среднее квадратичное отклонение, практически равна нулю.
Это правило называется правилом трех сигм.
Не практике считается, что если для какой – либо случайной величины выполняется правило трех сигм, то эта случайная величина имеет нормальное распределение.
Пример. Поезд состоит из 100 вагонов. Масса каждого вагона – случайная величина, распределенная по нормальному закону с математическим ожиданием 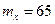 т. и средним квадратичным отклонением
т. и средним квадратичным отклонением 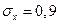 т. Локомотив может везти состав массой не более 6600 т, в противном случае необходимо прицеплять второй локомотив. Найти вероятность того, что второй локомотив не потребуется.
т. Локомотив может везти состав массой не более 6600 т, в противном случае необходимо прицеплять второй локомотив. Найти вероятность того, что второй локомотив не потребуется.
Второй локомотив не потребуется, если отклонение массы состава от ожидаемого (100×65 = 6500) не превосходит 6600 – 6500 = 100 т.
Т.к. масса каждого вагона имеет нормальное распределение, то и масса всего состава тоже будет распределена нормально. Получаем:
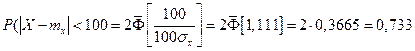 .
.
Пример. Нормально распределенная случайная величина Х задана своими параметрами – 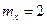 – математическое ожидание и
– математическое ожидание и 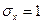 – среднее квадратическое отклонение. Требуется написать плотность вероятности и построить ее график, найти вероятность того, Х примет значение из интервала
– среднее квадратическое отклонение. Требуется написать плотность вероятности и построить ее график, найти вероятность того, Х примет значение из интервала 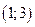 , найти вероятность того, что Х отклонится (по модулю) от математического ожидания не более чем на 2.
, найти вероятность того, что Х отклонится (по модулю) от математического ожидания не более чем на 2.
Плотность распределения определяется по формуле:
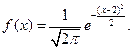
Найдем вероятность попадания случайной величины в интервал 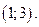
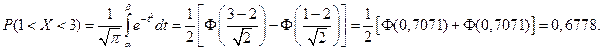
Найдем вероятность отклонение случайной величины от математического ожидания на величину, не большую чем 2:
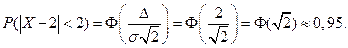
Тот же результат может быть получен с использованием нормированной функции Лапласа:
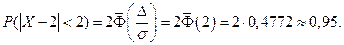
Дата добавления: 2015-09-29; просмотров: 2659;
