Иррациональные уравнения

Иррациональным уравнениемназывается уравнение, содержащее неизвестную под знаком корня или под дробным показателем. (В этом параграфе термин «корень» будет соответствовать операции извлечения корня с определенным показателем, в отличие от термина «решение»).

Основной метод решения таких уравнений – возведение обеих частей уравнения в одну и ту же степень, чтобы корни исчезли. Иногда приходится возводить в степень несколько раз. При этом следует анализировать, какие корни надо оставлять в левой части уравнения, а какие корни перенести в правую часть (если корней несколько). От этого часто зависит рациональность решения.

Поскольку корни нечетной степени определены для любых по знаку подкоренных выражений и принимают любые по знаку значения, то возведение уравнения в нечетную степень является равносильным преобразованием (т. е. мы не теряем решений и не получаем посторонних).

Корни с четным показателем 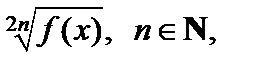определены для f(x)³ 0. Возведение уравнения, содержащего такие корни, в четную степень может изменить ОДЗ уравнения и привести к посторонним решениям. В таком случае итоговым моментом в решении уравнения является проверка полученных решений подстановкой в заданное уравнение. Проверка решения по ОДЗ такого уравнения недостаточна.

ОДЗ иррационального уравнения следует находитьв том случае, если предполагается, что она состоит только из нескольких чисел или может быть пустым множеством. Если ОДЗ состоит из одного, двух и т. д. чисел, то уравнение можно не решать, а эти числа проверять (являются ли они решением) подстановкой в заданное уравнение.

Если ОДЗ есть пустое множество, то уравнение не имеет решений.

При решении иррациональных уравнений используют также метод замены переменной и другие методы.

Если имеется уравнение вида 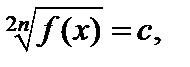где с < 0, то оно не имеет решений, так как корни с четным показателем понимаем в арифметическом смысле, т. е. как неотрицательные.