Приклад розв’язання задачі
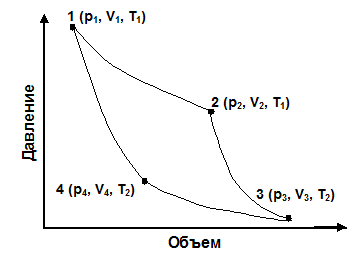 Дано:
Дано:
робоче тіло – вуглекислий газ (СО2)
V1 = 10 л = 10-2 м3
Р1 = 2·106 Па
Т1= 900 K
d = 0,33·10-9 м
M = 0,044 кг/моль
i = 6; n1= 3; n2= 1,5

Знайти:
1. Масу робочого тіла m.
2. Параметри станів (2) (3) (4).
3. Густину робочого тіла в стані (3) ρ3.
4. Середню довжину вільного пробігу молекул робочого тіла в стані (1) < l1>.
5. Коефіцієнт дифузії робочого тіла в стані (2) D2.
6. Середнє значення енергії поступального руху всіх молекул робочого тіла в стані (1) Eп .
7. Середнє значення енергії обертального руху всіх молекул робочого тіла в стані (1), Eоб .
8. Теплоємність робочого тіла ср, сv.
9. Значення робіт для окремих ділянок циклу.
10. Кількість теплоти, одержану робочим тілом від нагрівника Q1.
11. Кількість теплоти, передану робочим тілом охолоджувачу Q2.
12. Роботу, яку виконує теплова машина за один цикл А.
13. Коефіцієнт корисної дії теплової машини h.
14. Зміна внутрішній енергії для окремих ділянок циклу DU.
Маса m робочого тіла знайдемо з рівняння Менделєєва-Клапейрона для стану (1):
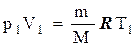 , (1)
, (1)
де P1,V1,T1 - тиск, об'єм, абсолютна температура для стану (1), М – молярна маса, R - універсальна газова стала.
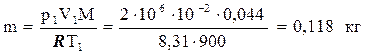
Ділянка (1) - (2) ізотермічне розширення при температурі T1. Рівняння Менделєєва - Клапейрона для стану (2):
 (2)
(2)
Зіставивши формули (1) і (2), одержимо: 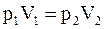
Звідси:
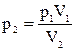 (3)
(3)
По умові завдання при ізотермічному розширенні (1) - (2) об'єм V2 зростає в n1 разів, тобто 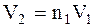 .
.
З формули (3) одержуємо:
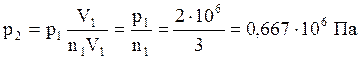
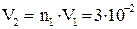 м3
м3
Ділянка (2) - (3) - адіабатне розширення в n2 разів. Згідно рівнянню для адіабатного процесу:
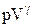 = const
= const
де 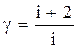 - показник адіабати.
- показник адіабати.
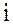 - число ступенів свободи молекули. Для одноатомних молекул (Ar, He) i=3, для двоатомних молекул (N2, O2) i=5, для трьохатомних молекул (CO2, H2O) i=6. (Увага! Для повітря прийняти i=5).
- число ступенів свободи молекули. Для одноатомних молекул (Ar, He) i=3, для двоатомних молекул (N2, O2) i=5, для трьохатомних молекул (CO2, H2O) i=6. (Увага! Для повітря прийняти i=5).
Для процесу (2) - (3) рівняння Пуассона приймає вигляд:
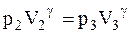
Знаходимо:
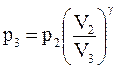 (4)
(4)
По умові завдання 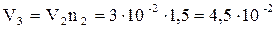 м3.
м3.
Тоді рівняння (4) прийме вигляд:
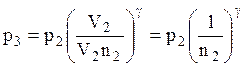
Обчислюємо показник адіабати:

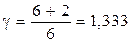
Знаходимо тиск в стану (3)
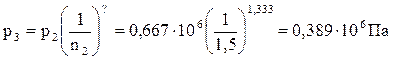
Точка 4 циклу знаходиться на перетині ізотерми (3) - (4) і адіабати (4) - (1). Для ізотерми (3) - (4) справедливе співвідношення:
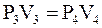
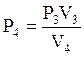 (5)
(5)
Для адіабати (4) - (1):
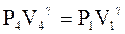 (6)
(6)
Підставляємо (5) в (6):
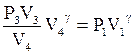
Після спрощення одержуємо:
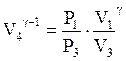
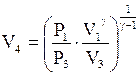
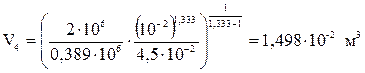
По формулі (5) обчислюємо P4:
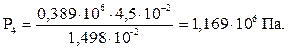
Для адіабатного процесу:
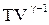 = const (7)
= const (7)
Тоді для адіабати (2) - (3) можна записати:
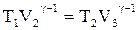 (8)
(8)
З формули (8) визначаємо температуру T2 достатку (3):
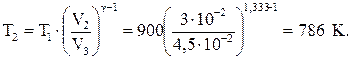
Параметри станів 1,2,3,4 приведені в таблиці:
| Стан | P, Па | V, м3 | T, К |
| P1 =2×106 | V1 = 10-2 | T1 = 900 | |
| P2 =0,667×106 | V2 = 3×10-2 | T2 = 900 | |
| P3 =0,389×106 | V3 = 4,5×10-2 | T3 = 786 | |
| P4 =1,169×106 | V4 = 1,498×10-2 | T4 = 786 |
Густина водяної пари  в стану (3):
в стану (3):
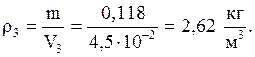
Середня довжина вільного пробігу 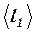 молекул в стані (1):
молекул в стані (1):
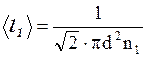 , (9)
, (9)
де 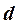 - ефективний діаметр молекул (таблична величина)
- ефективний діаметр молекул (таблична величина) 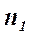 - концентрація молекул в стані (1)
- концентрація молекул в стані (1)
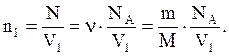 (10)
(10)
Тут 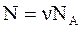 - число молекул,
- число молекул, 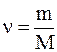 - число молей,
- число молей, 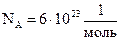 - число Авогадро. Підставляючи (10) в (9), обчислюємо середню довжину вільного пробігу молекул:
- число Авогадро. Підставляючи (10) в (9), обчислюємо середню довжину вільного пробігу молекул:
 (11)
(11)

Коефіцієнт дифузії D2 молекул водяної пари в стані (2):
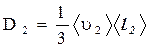 , (12)
, (12)
де 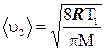 - середня швидкість молекул водяної пари в стані 2, -
- середня швидкість молекул водяної пари в стані 2, - 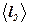 - середня довжина пробігу молекул в стані 2.
- середня довжина пробігу молекул в стані 2.
Для 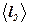 по аналогії з формулою (11) запишемо:
по аналогії з формулою (11) запишемо:

Після підстановки виразів 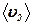 і <l
і <l 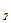 > в (12) одержуємо коефіцієнт дифузії в стані (2):
> в (12) одержуємо коефіцієнт дифузії в стані (2):
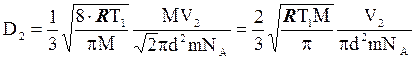
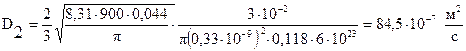
Середнє значення кінетичної енергії поступального руху всіх молекул водяної пари: при температурі Т1:
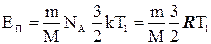 , (13)
, (13)
де 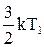 - середнє значення кінетичної енергії поступального руху однієї молекули.
- середнє значення кінетичної енергії поступального руху однієї молекули.
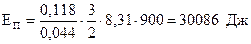
Середнє значення кінетичної енергії обертального руху молекул при температурі Т1:
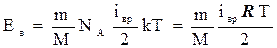
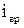 - число обертальних ступенів свободи молекул. Для одноатомних молекул
- число обертальних ступенів свободи молекул. Для одноатомних молекул 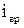 =0, для двоатомних молекул
=0, для двоатомних молекул 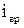 =2, для трьохатомних молекул
=2, для трьохатомних молекул 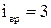 .
.
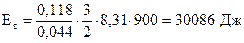
Теплоємність при сталому тиску для даної маси газу:
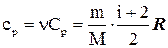
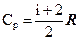 - молярна теплоємність ідеального газу при сталому тиску.
- молярна теплоємність ідеального газу при сталому тиску.
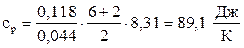
Теплоємність при сталому об'ємі для даної маси газу:
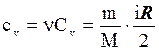
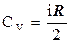 - молярна теплоємність ідеального газу при сталому об'ємі.
- молярна теплоємність ідеального газу при сталому об'ємі.
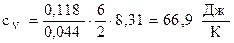
Робота ізотермічного процесу:
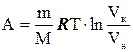 , (14)
, (14)
де Vн- початковий об’єм , Vк- кінцевий об’єм.
При ізотермічному розширенні 1 - 2 робота газу рівна:
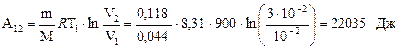
При ізотермічному стисненні 3 – 4 робота газу рівна:
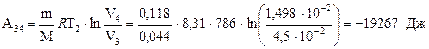
Робота адіабатного процесу рівна:
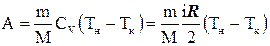 , (15)
, (15)
Робота адіабатного розширення 2-3:
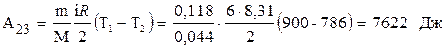
Робота адіабатного стиснення 4-1:
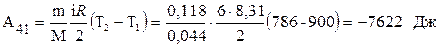
Робота A, що здійснюється тепловою машиною за один цикл становить: 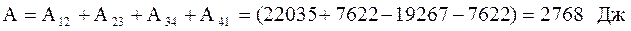 Визначимо кількість теплоти Q1, яку робоче отримало від нагрівника, і кількість теплоти Q2, віддано робочим тілом охолоджувачу.
Визначимо кількість теплоти Q1, яку робоче отримало від нагрівника, і кількість теплоти Q2, віддано робочим тілом охолоджувачу.
Згідно першому початку термодинаміки
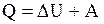 , (16)
, (16)
де Q - кількість теплоти, передана системі, DU - зміна внутрішньої енергії системи, А -робота, виконана системою.
Внутрішня енергія ідеального газу:
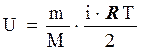

Зміна внутрішній енергії газу:
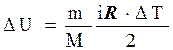 (17)
(17)
Робоче тіло одержує теплоту Q1 від нагрівника при ізотермічному розширенні (1) - (2). При цьому DU = 0. Тоді згідно рівняння (16):
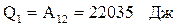
При ізотермічному стисненні (3) - (4) охолоджувачу віддається кількість теплоти:
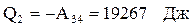
Адіабатні процеси 2-3 і 4-1 проходять без теплообміну з навколишнім середовищем. Тоді робота А, виконана за один цикл, буде рівна:
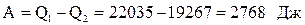
Це значення співпадає із значенням, одержаним вище шляхом підсумовування робіт для окремих ділянок циклу.
Коефіцієнт корисної дії теплової машини дорівнює відношенню роботи, здійсненої за один цикл, до кількості теплоти, отриманої від нагрівника:
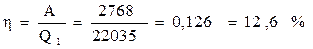
Для циклу Карно ККД можна визначити через температури нагрівника і охолоджувача:
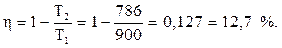
Для ізотермічних процесів (1) - (2) и (3) - (4) зміна внутрішньої енергії дорівнює:
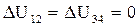
Оскільки при адіабатних процесах немає теплообміну з навколишнім середовищем, з формули (16) виходить:
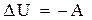
Тоді зміна внутрішній енергії при адіабатному розширенні (2) - (3) буде рівна:
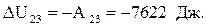
Зміна внутрішній енергії при адіабатному стисненні (4) - (1) рівна:

Дата добавления: 2015-09-29; просмотров: 1874;
