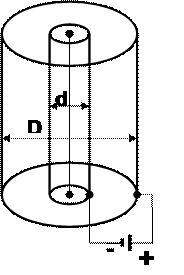
Приклад розв’язання задачі. 1. Залежність напруженості E електричного поля від відстані r до осі електродів.
 |
Дано:
 U = 48 кВ = 48×103 В
U = 48 кВ = 48×103 В
d = 2 мм = 2×10-3 м
D = 290 мм = 0,29 м
R = 0,9 мкм = 9×10-7 м
l = 3,5 м
r = 4000 кг/м3

Знайти:
1. Залежність напруженості E електричного поля від відстані r до осі електродів.
2. Залежність потенціалу j від відстані r до осі електродів.
3. Лінійну густину t електричних зарядів на електродах.
4. Прискорення а, яке отримує пилинка, що знаходиться посередині між електродами.
5. Електричну ємкість C електрофільтру.
6. Енергію електричного поля W фільтра.
7. Густину енергії електричного поля біля коронуючого w1 і осаджувального w2 електродів.
Електростатичне поле у фільтрі створюється коронуючим електродом. Напруженість Е електричного поля рівномірно зарядженого циліндра рівна:
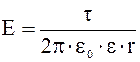 (1)
(1)
де (t - лінійна густина електричного заряду на циліндрі, 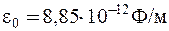 - електрична стала, r - відстань від осі циліндра, e - діелектрична проникність повітря, яку приймаємо рівною 1. Різниця потенціалів
- електрична стала, r - відстань від осі циліндра, e - діелектрична проникність повітря, яку приймаємо рівною 1. Різниця потенціалів 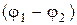 між коронуючим і осаджувальним електродами дорівнює:
між коронуючим і осаджувальним електродами дорівнює:
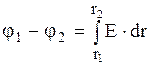 (2)
(2)
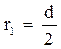 - радіус коронуючого електроду,
- радіус коронуючого електроду, 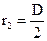 - радіус осаджувального електроду.
- радіус осаджувального електроду.
Після підстановки (1) в (2) і інтегрування отримаємо:
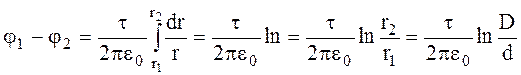 (3)
(3)
Осаджувальний електрод заземлений, тому його потенціал 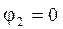 . Тоді потенціал коронуючего електроду
. Тоді потенціал коронуючего електроду 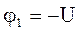 .
.
З формули (3) отримаємо:
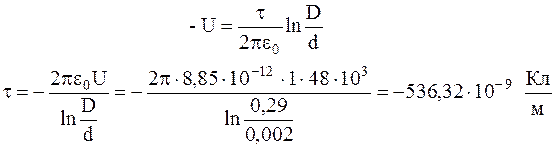
Перевірка одиниць вимірювань: 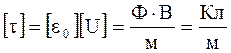
З урахуванням знайденого значення t по формулі (1) розрахуємо величину напруженості електричного поля Е залежно від відстані r. Значення r беруться в межах від 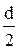 до
до 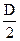 .
.
Перетворюючи формулу (3), отримаємо вираз для розрахунку залежності потенціалу j від відстані r :
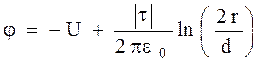 (4)
(4)
У формулі (4) величина t береться по абсолютному значенню. Розрахунок проводимо для різних значень r в межах від 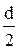 до
до 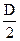 . Результати розрахунку представлені в таблиці (величина Е узята по абсолютному значенню).
. Результати розрахунку представлені в таблиці (величина Е узята по абсолютному значенню).
| r, мм | Е(r), кВ/м | j(r), кВ |
| -48 | ||
| -41,3 | ||
| -34,6 | ||
| -27,9 | ||
| -21,3 | ||
| -5,7 | ||
| 96,8 | -3,6 | |
| 80,7 | -1,8 | |
| 66,8 |
Прискорення пилинки а визначається по другому закону Ньютона:
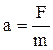 (5)
(5)
F - сила дії електричного поля на заряджену пилинку, m - маса пилинки.
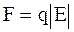 , (6)
, (6)
де q - заряд пилинки, E – напруженість електричного поля.
Маса пилинки 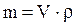 , де
, де 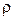 - густина пилинки,
- густина пилинки, 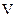 - об’єм пилинки. Вважаємо, що пилинка є кулькою з об’ємом
- об’єм пилинки. Вважаємо, що пилинка є кулькою з об’ємом 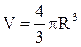 .
.
Тоді: 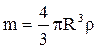 (7)
(7)
Вираз (5) з урахуванням формул (1), (6) и (7) прийме вигляд:
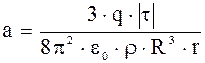 (8)
(8)
Якщо пилинка знаходиться посередині між електродами, то з урахуванням того, що 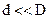 , відстань r від пилинки до осі циліндрів дорівнює:
, відстань r від пилинки до осі циліндрів дорівнює:
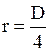 (9)
(9)
Підставивши (9) в (8), отримаємо:
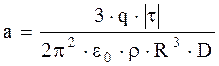 (10)
(10)
Дослідним шляхом встановлене наступне:
1) Якщо радіус пилинки  , то ії заряд дорівнює:
, то ії заряд дорівнює:
 (11)
(11)
Тут 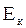 - напруженість електричного поля коронного розряду.
- напруженість електричного поля коронного розряду.
З урахуванням того, що для повітря 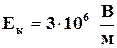 , формула (9) приймає вигляд:
, формула (9) приймає вигляд:
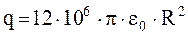 (12)
(12)
Після підстановки виразу (12) і чисельних значень констант e0 і p в формулу (10) отримаємо наступну формулу для обчислення прискорення пилинки:
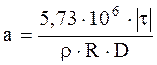 (13)
(13)
2) Якщо ж радіус пилинки R £ 1 мкм, то її заряд рівний:
 , (14)
, (14)
де 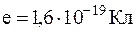 - елементарний електричний заряд.
- елементарний електричний заряд.
Після підстановки виразу (14) і чисельних значень констант e0 і p в формулу (10) отримаємо наступну формулу для обчислення прискорення пилинки:
: 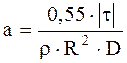 (15)
(15)
У даному завданні радіус пилинки R = 0,9 мкм. Тому прискорення пилинки обчислюється за формулою (15).
Дата добавления: 2015-09-29; просмотров: 1356;
