Приклад розв’язання задачі. Знайти: 1. Силу струму в соленоїді I. 2
|
 Дано:
Дано:
N = 1600
d =2,5 мм = 2,5×10-3 м
D= 11см = 0,11м
rэл = 65·10-9 Ом·м
ε = 40 B
r = 2 Ом
Тип частинки– Fe+++
М* = 56
U = 1250 B
a = 80 0
 | |||
 | |||
Сила струму знаходиться за законом Ома для замкнутого кола:
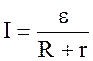 , (1)
, (1)
где  - ЭРС джерела, R- опір соленоїда, r- внутрішній опір джерела струму.
- ЭРС джерела, R- опір соленоїда, r- внутрішній опір джерела струму.
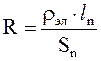 , (2)
, (2)
где ρэл - питомий опір, ln = πD·N - довжина дроту, πD- довжина одного витка, D- діаметр витка, N- кількість витків, 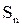 =
= 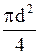 - площа поперечного перетину дроту, d- діаметр дроту.
- площа поперечного перетину дроту, d- діаметр дроту.
Після перетворень отримаємо:
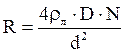
Знаходимо значення R і I:
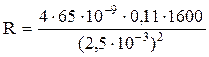 = 7,32 Ом.
= 7,32 Ом.
I = 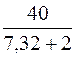 = 4,29 А
= 4,29 А
Потужність P1, що виділяється в соленоїді, і потужність P2, що виділяється на внутрішньому опорі джерела струму, визначається за законом Джоуля-Ленца:
P1= I2×R , P2= I2×r
Р1 = 4,292 ·7,32 = 134,72 Вт Р2 = 4,292 ·2 =36,81 Вт
Напруженість H магнітного поля в соленоїді:
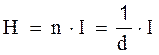 (3)
(3)
Тут n = 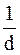 - число витків на одиницю довжини соленоїда.
- число витків на одиницю довжини соленоїда.
H = 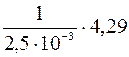 = 1716
= 1716 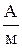
Індукція B магнітного поля в соленоїді
B= 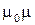 H (4)
H (4)
Тут 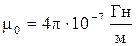 - магнітна стала,
- магнітна стала, 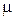 - магнітна проникність середовища. Приймаємо
- магнітна проникність середовища. Приймаємо 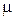 =1.
=1.
B = 4 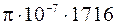 = 21564×10-7 Тл
= 21564×10-7 Тл
Магнітний потік Ф через поперечний перетин соленоїда S рівний:
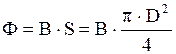 (5)
(5)
Ф = 
Потокосчіплення визначаємо за формулою:
Ψ = Ф×N = 205×10-7×1600 = 328×10-4 Вб (6)
Індуктивність соленоїда L дорівнює:
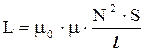 , (7)
, (7)
де 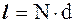 - довжина соленоїда.
- довжина соленоїда.
Після перетворень формула (7) приймає вигляд:
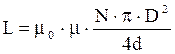 (8) L =
(8) L = 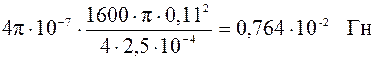
Якщо заряджена частинка прискорюється електричним полем з різницею потенціалів U, то вона набуває швидкості v, яку можна знайти з умови:
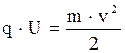 (9)
(9)
Тут q - заряд частинки, m – маса частинки, q·U - робота сил електричного поля по прискоренню заряду, (mv2)/2 - кінетична енергія частинки після прискорення. З виразу (9) знаходимо швидкість частинки:
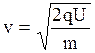 (10)
(10)
Увага! 1) Якщо частинкою в завданні є електрон, протон або a-частинка, то її маса m береться з таблиці.
2) Якщо частинкою в завданні є іон, то його маса m обчислюється за формулою: 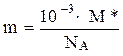 , де М* - відносна атомна маса іона (береться з таблиці), NА = 6×1023 1/моль - число Авогадро.
, де М* - відносна атомна маса іона (береться з таблиці), NА = 6×1023 1/моль - число Авогадро.
3) Якщо частинкою в завданні є електрон або протон, то її заряд q = 1,6×10-19 Кл.
4) Якщо частинкою в завданні є a-частинка, то її заряд q = 3,2×10-19 Кл.
5) Якщо частинкою в завданні є іон, то його заряд q = Z×1,6×10-19 Кл, де Z – ступінь іонізації даного іона.
У даному завданні частинкою є тричі іонізований іон заліза 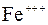 . Заряд цього іона дорівнює:
. Заряд цього іона дорівнює:
q = 3×1,6×10-19 = 4,8×10-19 Кл (11)
Масу іона заліза m визначаємо за формулою:
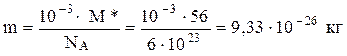 (12)
(12)
Підставивши (11) і (12) в рівняння (10), знайдемо швидкість іона заліза, що влітає в соленоїд:
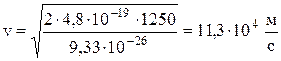
Розгледимо рух зарядженої частинки в магнітному полі соленоїда. Вона влітає із швидкістю v під кутом a з віссю соленоїда і відповідно з вектором магнітної індукції B магнітного поля соленоїда. В загальному випадку, коли a ¹ 900, в результаті дії на заряд сили Лоренца він рухатиметься по спіралі, яка характеризується радіусом Rсп і кроком f спіралі.
Розкладемо вектор швидкості на дві складові: Vn, перпендикулярну до напряму поля, і Vt, паралельну цьому напряму.

З рисунка виходить: 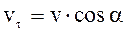 ,
, 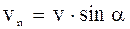 .
.
Значення складових швидкості Vn и Vτ визначають величини Rсп и f відповідно.
Використовуючи формули для сили Лоренца і доцентрової сили і враховуючи, що Fл = Fц, отримаємо вираз для обчислення радіусу спіралі Rсп .
Fл = vn×q×B = v×q×B×sin a
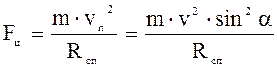
Прирівнявши праві частини цих рівностей, отримаємо:
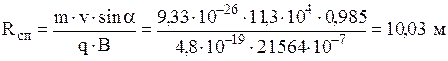
Крок спіралі f обчислюється по формулі:
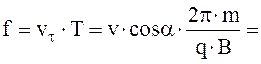
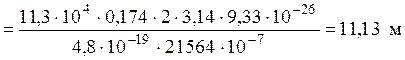
Тут Т – період обертання частинки по спіралі.
Енергія магнітного поля:
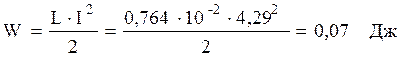
Густина енергії магнітного поля:
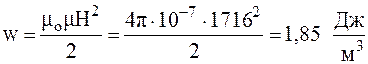
Дата добавления: 2015-09-29; просмотров: 937;
