Трансфинитное отображение

Трансфинитное отображение (transfmite mapping) позволяет отображать области (с тремя или четырьмя сторонами в двумерном случае или коробочного типа в трехмерном) на регуляризованную область без всяких геометрических погрешностей. Другими словами, точки, находящиеся на границе исходной области, всегда отображаются на границу регуляризованной области.

Четырехстороннюю область (рис. 8.23, а) легко отобразить на единичный квадрат в пространстве параметров иv (рис. 23, б) методом, который уже использовался при выводе уравнения лоскута Куна в главе 7. Отображение четырехсторонней области на регуляризованную выражается формулой

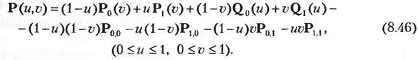
Затем на параметрическую область накладывается решетка (см. рис. 23, б), и координаты u и v точек решетки подставляются в уравнение (8.46), с тем чтобы получить координаты точек узлов. Значения u и v можно подобрать таким образом, что плотность ячеек в одних участках области будет больше или меньше, чем в других.

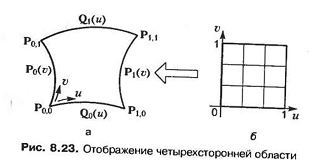
Область с тремя сторонами столь же легко разбить на сетку из троеугольных элементов, используя трилинейную интерполяционную функцию, чему посвящена работа. Трехсторонняя областьна рис. 8.24 (а) может быть отображена на параметрическую область с рис. 8.24 (б) функцией

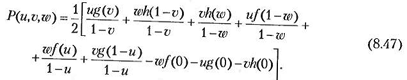
Параметрическая область задания уравнения (8.47) описывается следующим уравнением:

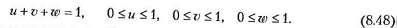
В этом случае параметрическая область может быть поделена на ячейки заданинием набора последовательных значений u и v от 0 до 1 и вычислением соответствующих значении w для каждой пары и и v.

Трансфинитное отображение трехмероной области выводится тем же образом, что и отображение четырехсторонней плоской области. Единственное отличие состоит в том, что сопрягать приходится шесть уравнений граничных поверхностей, а не два уравнения граничных кривых.