Отображение нечетких множеств.
Четкие отображения. Обычным, четким отображением (многозначным, полиморфным) 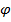 множества Х в множество Y,
множества Х в множество Y, 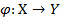 называется , произвольное подмножество декартового произведения
называется , произвольное подмножество декартового произведения 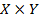 , то есть
, то есть 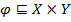 . Множество Х называется областью определений отображения, а Y – областью значений. Для фиксированного элемента х*
. Множество Х называется областью определений отображения, а Y – областью значений. Для фиксированного элемента х* 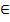 Х области определения отображения его образом по отображению
Х области определения отображения его образом по отображению 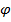 называется множество
называется множество 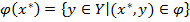 .
.
Образом множества A⊑X по отображению 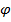 называется объединение образов всех элементов А, то есть множество
называется объединение образов всех элементов А, то есть множество 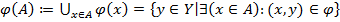 .
.
Если каждому элементу х 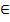 Х отвечает один и лишь один элемент
Х отвечает один и лишь один элемент 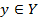 и одновременно выполняется обратное утверждение, то есть каждому элементу
и одновременно выполняется обратное утверждение, то есть каждому элементу 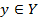 отвечает один и лишь один элемент х
отвечает один и лишь один элемент х 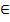 Х, то такое отображение является изоморфным, или взаимно однозначным. Если каждому элементу х
Х, то такое отображение является изоморфным, или взаимно однозначным. Если каждому элементу х 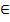 Х соответствует один и лишь один элемент
Х соответствует один и лишь один элемент 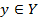 , но обратное утверждение не выполняется, то отображение является гомоморфным, то есть для каждого элемента х
, но обратное утверждение не выполняется, то отображение является гомоморфным, то есть для каждого элемента х 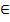 Х существует один и лишь один образ, но вместе с тем несколько элементов х
Х существует один и лишь один образ, но вместе с тем несколько элементов х 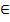 Х могут иметь один и тот же образ.
Х могут иметь один и тот же образ.
Обратное отображение 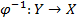 для отображения
для отображения 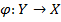 называется такое отображение, для которого
называется такое отображение, для которого 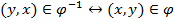 . Образ элемента y*
. Образ элемента y* 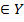 при обратном отображении
при обратном отображении 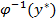 он является подмножеством множества Х.
он является подмножеством множества Х.
Принцип обобщения Л.Заде. Способ расширения области определения на класс нечетких множеств можно получить с помощью принципа обобщения. Л.Заде предложил следующий принцип обобщения, который основывается на определении понятия образа нечеткого множества при условии обычного четкого отображения. Пусть 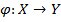 – заданное отображение и пусть А – некоторое нечеткое подмножество множества Х с функцией принадлежности
– заданное отображение и пусть А – некоторое нечеткое подмножество множества Х с функцией принадлежности 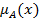 . Согласно принципа обобщения Л.Заде образ А при отображении
. Согласно принципа обобщения Л.Заде образ А при отображении 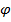 определяется как нечеткое подмножество множества Y, что является совокупностью пар следующего вида:
определяется как нечеткое подмножество множества Y, что является совокупностью пар следующего вида: 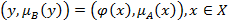 , где
, где 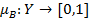 – функция принадлежности образа. Таким образом функцию принадлежности
– функция принадлежности образа. Таким образом функцию принадлежности 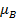 можно записать следующим образом :
можно записать следующим образом : 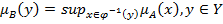 , где множество
, где множество 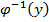 для произвольного фиксированного
для произвольного фиксированного 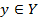 является следующей
является следующей 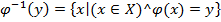 , то есть является множеством всех тех элементов х
, то есть является множеством всех тех элементов х 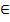 Х, образом каждого из которых при отображении
Х, образом каждого из которых при отображении 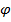 является элемент y.
является элемент y.
Образом В нечеткого множества А в Х при условии нечеткого отображения 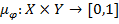 называется нечеткое множество, которое имеет следующую принадлежность
называется нечеткое множество, которое имеет следующую принадлежность  .
.
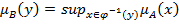 соответствует определению образа, на котором основывается принцип обобщения Л.Заде.
соответствует определению образа, на котором основывается принцип обобщения Л.Заде.
Многомерные нечеткие отображения и прообразы. Если заданное нечеткое отображение 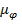 зависит от n переменных, то есть имеет вид
зависит от n переменных, то есть имеет вид 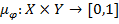 , где
, где 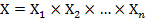 – декартовое произведение соответствующих множителей, и на множестве Х задано нечеткое подмножество
– декартовое произведение соответствующих множителей, и на множестве Х задано нечеткое подмножество 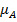 , то в общем случае функция принадлежности этого подмножества будет иметь следующий вид
, то в общем случае функция принадлежности этого подмножества будет иметь следующий вид 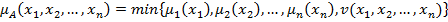 , где
, где 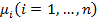 и v-заданные нечеткие подмножества соответствующих множеств
и v-заданные нечеткие подмножества соответствующих множеств 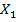 b X. Эта запись означает, что множество является «совокупностью» всех наборов
b X. Эта запись означает, что множество является «совокупностью» всех наборов  таких, что
таких, что 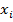 «принадлежит» нечеткому множеству
«принадлежит» нечеткому множеству 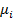 , а
, а 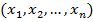 – нечеткому множеству v.
– нечеткому множеству v.
Используя принцип обобщения в этом случае, получаем следующий вид для функции принадлежности нечеткого множества 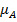 :
: 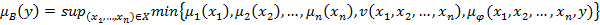 .
.
Прообразом А нечеткого множества В в Y для нечеткого отображения 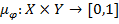 , называется объединение всех нечетких множеств, образы которых для этого отображения принадлежат (являются подмножествами) нечеткого множества В.
, называется объединение всех нечетких множеств, образы которых для этого отображения принадлежат (являются подмножествами) нечеткого множества В.
Нечеткое множество А – прообраз множества В – имеет следующую функцию принадлежности 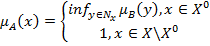 , где множества
, где множества 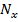 и
и 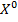 определяются из следующих соотношений:
определяются из следующих соотношений: 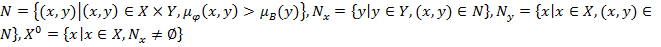 .
.
Дата добавления: 2015-09-11; просмотров: 3469;
