Построение элементов

На этом этапе осуществляется соединение узлов, в результате чего получаются элементы, которые не должны перекрываться, но должны покрывать всю площадь объекта. Мы рассмотрим метод Ли, который может давать четырехугольные элементы. Однако наиболее популярным методом соединения узлов является метод триангуляции Делоне. В нижеследующем рассмотрении мы будем учитывать только те элементы, у которых узлы находятся в вершинах. Если задача требует использования элементов с промежуточными узлами, их легко можно построить по элементам с узлами в вершинах. Поэтому мы не будем исследовать промежуточные узлы во всех описываемых ниже методах.

□ Метод Ли . Согласно этому методу, на объект накладывается квадратная сетка, размер ячеек которой соответствует ожидаемому размеру элементов. Затем узлы, полученные на предыдущем этапе, связываются с ячейками этой сетки. Ячейки и соответствующие им узлы перебираются по столбцам слева направо и сверху вниз. Внутри ячейки узлы упорядочиваются по возрастанию абсцисс. Узлы с одинаковыми абсциссами сортируются но возрастанию ординат. Узлы перебираются последовательно, причем из соседних узлов выбираются такие, с которыми данный узел образует «хороший» четырехугольник. Если же четырехугольник оказывается «плохим», вместо него формируется треугольник.

□ Триангуляция Делоне . Это, пожалуй, наиболее популярный метод формирования треугольников путем соединения узлов, поскольку он максимизирует сумму наименьших углов во всех формируемых треугольниках. Иначе говоря, данный метод триангуляции ориентирован на то, чтобы по возможности избегать формирования узких треугольников.

Триангуляция Делоне обычно начинается с диаграммы Вороного или полигонов Дирихле. Диаграмма Вороного ( Voronoi diagram) множества N точек Р_i (i= 1, 2,.... N)сос тоит из N многоугольников (многогранников, если задача решается в трех измерениях) V_t, центры которых находятся в точках Р_i причем многоугольники эти представляют собой геометрическое место точек, для которых данный узел iявляется ближайшим. Математическая запись этого утверждения относительно многоугольника V_i выглядит следующим образом:

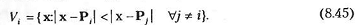
Многоугольник (многогранник) V_i является выпуклым. Он ограничивается прямыми (плоскостями), проходящими через середины отрезков, соединяющих узел P_j с его соседями, и перпендикулярными этим отрезкам. Такое разбиение двумерного или трехмерного пространства называется полигонами Дирихле (Dmchlet tesselation).Каждый многоугольник (многогранник) Вороного связан с одним определенным узлом. Построив диаграмму Вороного, мы можем перейти к созданию треугольных (тетраэдрических) элементов, соединяя точки соседних многоугольников (многогранников) Вороного. Диаграмму Вороного и результат триангуляции для десяти узлов на плоскости демонстрирует рис. 8.11.

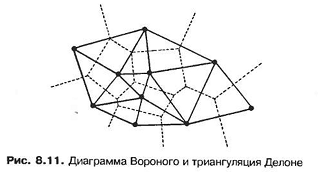
Триангуляция Делоне может производиться непосредственно на наборе точек (узлов) с использованием алгоритма двухмерной триангуляции Ватсона f без предварительного построения диаграммы Вороного. Согласно этому алгоритму, три точки, не лежащие на одной прямой, объединяются в треугольник, если окружность, проведенная через эти точки (описанная окружность для будущего треугольника), не захватывает никаких других точек. Алгоритм реализуется следующим образом. Сначала строится треугольник Т₀, внутри которого находятся все узлы. Вершинами этого треугольника могут быть и точки, не являющиеся узлами. Затем осуществляется перебор узлов из полного их множества, и для каждого узла ищутся треугольники, такие, что описанная вокруг них окружность захватывает данный узел. Эти л реугольники (называемые пересеченными) в дальнейшем не рассматриваются. На рис. 8.12, б они обозначены знаком X. Затем вместо них строятся новые треугольники, образуемые соединением добавленного узла с вершинами пересеченных треугольников (рис. 8.12, в).

На заключительном этапе удаляются треугольники, полученные соединением узлов с дополнительными точками, введенными на первом этапе для построения треугольника Т₀. Эта процедура легко обобщается на трехмерное пространство путем перехода к использованию описанных сфер для четырех узлов вместо окружностей для трех узлов. Однако в трехмерном случае триангуляция Делоне может давать очень узкие тетраэдры, тогда как в двухмерном случае алгоритм обеспечивает в некотором смысле оптимальную триангуляцию данного набора точек.

Топологическое разбиение

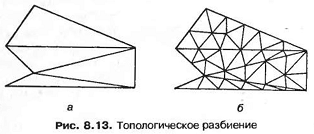
Метод топологического разбиения (topology decomposition approach) для двумерного случая был разработан Ворденвебером. Согласно этому методу объект аппроксимируется многоугольником, который, в свою очередь, разбивается на множество крупных элементов (gross elements) соединением его вершин до получения треугольников (рис. 8.13, а). Затем крупные элементы разбиваются на более мелкие до тех пор, пока не будет достигнута желаемая плотность ячеек сетки (рис. 8.13, б). Размеры и форма элементов в данном алгоритме не могут быть заданы пользователем, поскольку крупные элементы зависят только от исходной топологии объекта, в частности от распределения вершин. Вершины, относящиеся к одному крупному элементу, могут быть найдены методом триангуляции Делоне, описанным в предыдущем разделе.

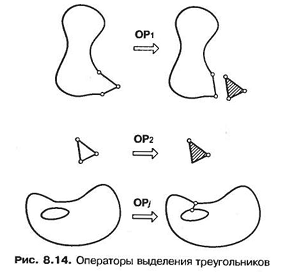
Для формирования набора треугольников по исходным вершинам Ворденвебер разработал операторы, аналогичные операторам Эйлера, применяемым в объемном моделировании. Первый оператор Ворденвебера ОР_j применяется к объекту для удаления имеющихся в нем отверстий (рис. 8.14). Затем по вершинам объекта строятся треугольники, которые отделяются от объекта рекурсивным применением оператора ОР₁,пока вершин не останется всего три. Последний треугольник строится оператором ОР₂.

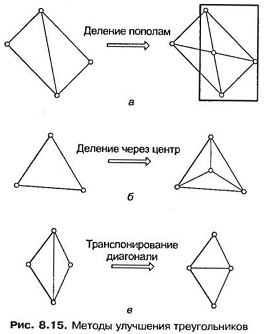
После преобразования объекта в набор крупных треугольников осуществляется их детализация, позволяющая достичь требуемой плотности сетки. Детализация может быть проведена тремя методами (рис. 8.15). На рис. 8.15, а показан метод, применяемый в том случае, если два узких треугольника имеют общую длинную сторону. На общей стороне создается еще один узел, после чего соседние треугольники делятся на части путем соединения их вершин с новым узлом. На рис. 8.15, б показано, как большой треугольник делится путем добавления нового узла в его центре тяжести. В результате деления перечисленными двумя методами может получиться так, что узкие треугольники, уже отвечающие требованиям к плотности сетки, будут иметь общую сторону (рис. 8.15, в). В этом случае качество сетки может быть повышено благодаря использованию второй диагона- ли четырехугольника, образуемого вершинами двух исходных треугольников.

Учтите, что результат анализа методом конечных элементов может быть недостаточно точным, если в сетке будет слишком много узких треугольников.

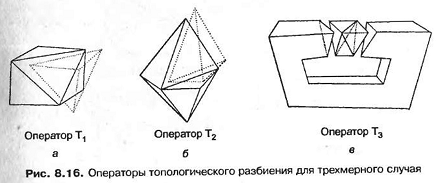
Метод топологического разбиения может быть обобщен на трехмерный случай.. Объект аппроксимируется многогранником, который разбивается на тетраэдрические элементы путем последовательного соединения вершин. Затем тетраэдрические элементы измельчаются делением на более мелкие тетраэдрические элементы. By и Томасма предложили операторы, аналогичные операторам Ворденвебера, для облегчения процесса построения тетраэдрических элементов. Эти операторы, действие которых демонстрируется на рис. 8.16, используются в следующем порядке. Сначала оператор Т₃ применяется к самому объекту для устранения отверстий в нем (рис. 8.16, в). Обратите внимание, что эта операция приводит к появлению двух побочных тетраэдров. Затем от объекта отделяются выпуклые углы, в которых смыкаются три ребра (такие углы называются выпуклыми трехвалентными вершинами). Это делает оператор Т₁(рис. 8.16, а). Оператор Т, применяется рекурсивно до тех пор, пока не останется ни одной выпуклой трехвалентной вершины. Если ни одна из вершин не является выпуклой трехва лентной, применяется оператор Т₂, выделяющий из объекта тетраэдр (рис. 8.16, б). После его применения образуются новые выпуклые трехвалентные вершины, поэтому снова применяется оператор T₁ Процедура продолжается до тех нор. пока от объекта не останется один тетраэдр.

Геометрическое разбиение

Методы геометрического разбиения (geometry decomposition approach) делятся на рекурсивные и итеративные. Мы расскажем только о рекурсивных методах, поскольку они могут использоваться и в трехмерном случае.

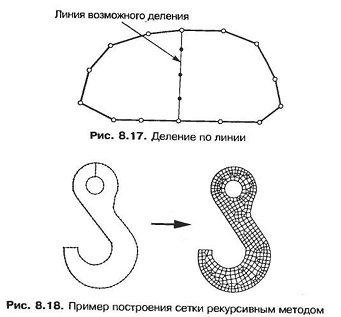
Метод рекурсивного геометрического разбиения состоит в построении треугольных или четырехугольных элементов на плоскости. Сначала исходный объект разбивается на выпуклые части вручную или автоматически. Автоматическое разбиение объекта на выпуклые части описано в работе Байката. Па границах выпуклых частей ставятся узлы в соответствии с требуемой плотностью конечной сетки. Затем каждая выпуклая часть делится пополам приблизительно посередине «длинной оси» (рис. 8.17), после чего на этой оси также ставятся узловые точки. Производится рекурсивное деление обеих половинок до гех пор, пока они не станут четырехугольниками или треугольниками. В некоторых вариантах метода деление производится до тех нор, пока в остатке не получатся шестиугольники или восьмиугольники, которые разбиваются на треугольные или четырехугольные элементы в соответствии с заранее заготовленными схемами. В этом случае элементы могут получиться более одинаковыми. Построение сетки рекурсивным методом иллюстрирует рис. 8.18.

Описанный метод может быть обобщен на трехмерный случай. Объект делится на два объемных тела по плоскости лучшего сечения до тех пор, пока все подобъекты не превратятся в тетраэдры. В отличие от двумерного случая, где в резуль- тате рекурсивного деления может получиться четырехугольник, в трехмерном случае невозможно получение шестигранников непосредственно в результате рекурсивного деления. Однако при желании можно разбить каждый тетраэдр на четыре шестигранника (кирпичика).

Решеточные методы

Решеточные методы (grid-based approaches) основаны на том, что решетка выглядит подобно сетке и может быть преобразована в последнюю при условии, что ячейки сетки вдоль границ объекта будут превращены в элементы. В общем случае более мелкая решетка дает сетку лучшего качества, поскольку в такой решетке доминируют внутренние ячейки правильной формы. Разновидности решеточных методов отличаются друг от друга главным образом методом создания граничных элементов.

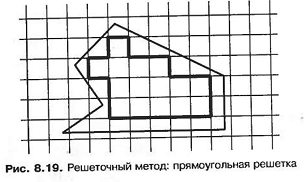
По всей видимости, первым решеточным методом был метод Такера и его коллег. Согласно этому методу на объект накладывается треугольная решетка, причем все точки решетки, оказывающиеся вне объекта, удаляются, в результате чего получается зигзагообразная граница. Точки на этой границе перемещаются на границу объекта, что дает готовую сетку. Кикучи расширил этот метод для создания сеток, состоящих главным образом из четырехугольников, однако содержащих некоторое количество треугольников. Он использовал прямоугольную решетку (рис. 8.19). Одним из недостатков обоих методов является исчезновение мелких деталей, размеры которых сравнимы с расстоянием между линиями решетки. В других методах точки на границе решетки не перемещаются на границу объекта. Вместо этого между зигзагообразной границей решетки и границей объекта создаются треугольные элементы, для чего используется алгоритм триангуляции.

Йерри и Шипхард для создания сеток воспользовались квадрантным деревом Квадрантное дерево представляет собой двумерный аналог октантного, о котором говорилось в главе 5. Это дерево позволяет представить двумерный объект (рис. 8.20, а) в виде набора квадрантов различного размера путем рекурсивною деления исходного квадранта, содержащего данный объект. Процесс деления объекта иллюстрирует рис. 8.20, б, а квадрантное дерево, описывающее процесс деления, изображено на рис. 8.20, в. Сетка строится следующим образом.

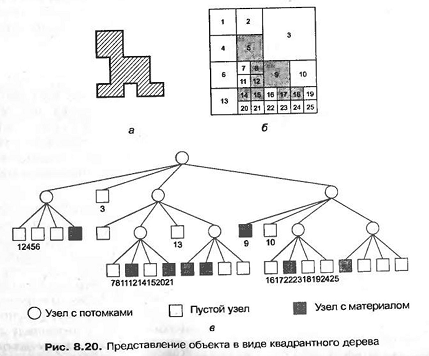
1. Создается исходный (корневой) квадрант, содержащий объект целиком внутри себя. Этот квадрант делится на четыре квадранта путем деления каждой его стороны пополам. Затем квадранты классифицируются по положению относительно объекта. Если квадрант не лежит целиком внутри или снаружи объекта, он делится дальше. Процесс деления продолжается до тех пор, пока не будет удовлетворено требование к плотности сетки, после чего берутся квадранты, либо лежащие целиком внутри объекта, либо имеющие с ним общие точки. Если рассматриваются квадранты, имеющие с объектом общие точки, их приходится модифицировать таким образом, чтобы они содержали только внутренние части объекта. Объект, состоящий из квадрантов, лежащих целиком внутри него, а также модифицированных квадрантов, имеющих с ним общие точки, будет выглядеть так, как показано на рис. 8.21, а.

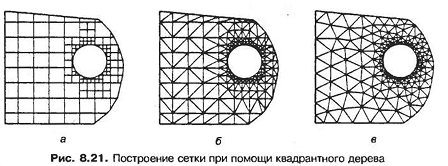
2. Каждый модифицированный квадрант делится на треугольные элементы в соответствии с предварительно заготовленными схемами в зависимости от его формы. Квадранты, лежащие полностью внутри объекта, также делятся на части для обеспечения согласования с соседними ячейками. Два соседних элемента называются согласующимися, если у них имеется целое общее ребро (в трехмерном случае — общая грань). Полученная этим методом сетка изображена на рис. 8.21, б.

3. Положения узлов корректируются так, чтобы улучшить форму ячеек. Результат сглаживания сетки демонстрирует рис. 8.21, в. Метод сглаживания будет описан позже.

Описанный метод был расширен на три измерения при помощи окгантного дерева Частично заполненные октанты модифицируются таким образом, чтобы лежать целиком внутри объекта, после чего разбиваются на тетраэдры, точно так же, как в двумерном случае квадранты разбивались на треугольники. Тетраэдры должны быть согласованы с соседними октантами и удовлетворять требованию к плотности ячеек. С учетом всех возможных случаев для этого требуется чрезвычайно сложный алгоритм. Вообще говоря, разбиение модифицированного квадранта в двумерном случае — тоже непростая задача.

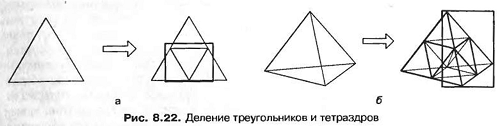
Джан и Ли предложили новый метод, согласно которому нужно начинать с треугольного корня (или тетраэдрического в трехмерном случае). Это позволяет избежать описанных выше затруднений. В этом случае квадрантное дерево будет аппроксимацией объекта треугольниками, а октантное дерево — тетраэдрами. Деление треугольного корня на четыре маленьких треугольника показывает рис. 8.22, а, а деление тетраэдрического корня на восемь тетраэдров — рис. 8.22,6.

Отображаемые элементы

Метод отображаемых элементов(mapped element approach) используется в большинстве коммерческих генераторов сеток. Этот метод требует деления объекта на области со специфической топологией. В двух измерениях области могут иметь три или четыре стороны, в трех измерениях области являются чем-то вроде коробок. В каждой области сетка строится автоматически путем отображения данной области на регуляризованную область (правильный треугольник или квадрат в двумерном случае и куб в трехмерном). Регуляризованная область делится на части с учетом ожидаемой плотности сетки, после чего отображается обратно на исходную область. Полная сетка получается слиянием сеток отдельных областей. На границах соседних областей количество узлов должно быть одинаковым, чтобы сетка получилась согласованной. Выполнение этого требования может обеспечиваться как вручную, так и алгоритмически в процессе построения сеток соседних областей.

Методов отображения существует достаточно много. Приведем в качестве примера два типичных метода: трансфинитное отображение и изопараметрическое отображение.