Критические условия хранения различных видов растительного сырья

№ п/п	Наиме­нование продук­та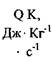
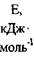
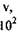
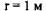
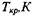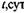
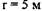
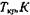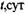
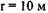
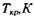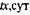
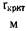
	Травя­ная мука	121-1015		1,75	357,73	-	329,45	-	318,53	-
	Шрот подсол­нечный	3,79- 106	43,2	2,27	267,61	2,4	225,92	2,2	211,84	2,2	0,39
	Жмых подсол­нечный	1,51 106	42,0	1,2	274,44		229,48	3,6	214,50	3,5	0,5
	Шрот соевый	4,36- 109	47,3	1,85	292,61		247,03	9,2	231,64	9,1	0,8
	Мука пшенич­ная	1,94- 1010	81,2	3,02	348,88	-	310,45	-	296,42	1387, 6	8,4
	Отруби пшенич­ные	4,1 108	60,9	2,27	303,05		264,66	17,7	251,01	17,2	1,12
	Мука из ячменя	2,04-109	73,6	2,61	344,91	-	303,61	-	288,76	548,1	5,63
	Дрожжи кормо­вые	7,93- 10ю	83,4	3,35	340,15		304,53		291,41	650,6	6,25
	Комби­корм для свиней	8,89' 10й	93,5	1,41	352,05		317,92		305,18		8,1
	Комби­корм для птиц	3,79- 109	71,6	1,78	326,35		288,31		274,57	120,6	2,8

Глава 3, Возникновение процессов горения

Учет функции Ф(Bi) в уравнении (3.93) позволяет существенно уменьшить неточность, возникающую в результате апроксимации распре­деления температуры в горючей системе параболой второго порядка.

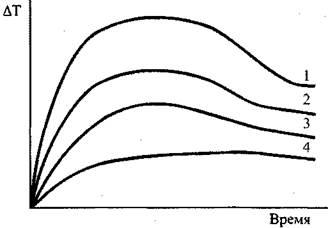
Рис. 3.12. Кинетические кривыеразогревов: 1-447 К; 2-450 К, 3-456; 4-458.

Для расчета критических значений температуры (T) и характерного размера (r) в уравнении (3.93) необходимы значения величин кинетиче­ских параметров: Е, Ко и v. (определение этих параметров осуществляется графоаналитическим способом по методу термического анализа из экс­периментальных кривых " 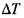- время" (Рис. 3.12).

Разработанная математическая модель позволяет рассчитывать ус­ловия самовозгорания и выполнить прогноз поведения насыпей дисперс­ной горючей массы любого размера и любой формы.

Результаты расчетов для широкого круга продуктов растительного происхождения представлены в табл. 3.2.

Данные табл. 3.2 показывают, что благодаря предложенной схеме расчета условие теплового самовозгорания можно не только установить ряд потенциальной опасности различных видов горючего дисперсного материала, но и прогнозировать критические условия их хранения (время индукции, размеры насыпи).

Необходимость обработки большого числа термических кривых де­лает описанный метод достаточно трудоемким и затрудняет его использо­вание для быстрого получения необходимой информации. В связи с этим

Корольченко А.Я. Процессы горения и взрыва______________________

разрабоганы алгоритмы и программа для расчета критических параметров на персональной ЭВМ. Это позволяет оперативно рассчитывать критиче­ские параметры процесса самовозгорания дисперсных горючих материа­лов и осуществлять прогноз их поведения в процессе переработки, транс­портировки и хранения.

Таблица 3.3. Сравнение расчетных и экспериментальных значений температуры