Гомогенное, гетерогенное и диффузионное горение
Перечисленные в предыдущем разделе физические явления наблюдаются в самых разнообразных процессах, различающихся как по природе химических реакций, так и по агрегатному состоянию участвующих в горении веществ.
Различают гомогенное, гетерогенное и диффузионное горение.
Глава 1. Основные понятия теории горения
К гомогенному относится горение предварительно перемешанных газов*. Многочисленными примерами гомогенного горения являются процессы сгорания газов или паров, в которых окислителем является кислород воздуха: горение смесей водорода, смесей оксида углерода и углеводородов с воздухом. В практически важных случаях не всегда выполняется условие полного предварительного перемешивания. Поэтому всегда возможны комбинации гомогенного с другими видами горения.
Гомогенное горение может быть реализовано в двух режимах: ламинарном и турбулентном. Турбулентность ускоряет процесс горения за счет дробления фронта пламени на отдельные фрагменты и соответственно увеличения площади контакта реагирующих веществ при крупномасштабной турбулентности или ускорения процессов те-пломассопереноса во фронте пламени при мелкомасштабной. Турбулентному горению присуща автомодельность: турбулентные вихри увеличивают скорость горения, что приводит к увеличению турбулентности.
Все параметры гомогенного горения проявляются и в процессах, в которых окислителем выступает не кислород, а другие газы. Например, фтор, хлор или бром.
При пожарах наиболее распространены процессы диффузионного горения. В них все реагирующие вещества находятся в газовой фазе, но предварительно не перемешаны. В случае горения жидкостей и твердых веществ процесс окисления горючего в газовой фазе происходит одновременно с процессом испарения жидкости (или разложения твердого материала) и с процессом смешения.
Простейшим примером диффузионного горения является горение природного газа в газовой горелке. На пожарах реализуется режим турбулентного диффузионного горения, когда скорость горения определяется скоростью турбулентного смешения.
При этом различают макросмешение и микросмешение. Процесс турбулентного смешения включает последовательное дробление газа на все более малые объемы и перемешивание их между собой. На последней стадии окончательное молекулярное смешение происходит молекулярной диффузией, скорость которой увеличивается по мере уменьшения масштаба дробления. По завершении макросмешения
* Подобное горение зачастую называют кинетическим.
Корольченко А.Я. Процессы горения и взрыва
скорость горения определяется процессами микросмешения внутри малых объемов горючего и воздуха.
Гетерогенное горение происходит на поверхности раздела фаз. При этом одно из реагирующих веществ находится в конденсированном состоянии, другое (обычно кислород воздуха) поступает за счет диффузии газовой фазы. Обязательным условием гетерогенного горения является очень высокая температура кипения (или разложения) конденсированной фазы. При несоблюдении этого условия горению предшествует испарение или разложение. От поверхности в зону горения поступает поток пара или газообразных продуктов разложения, и горение происходит в газовой фазе. Такое горение можно отнести к диффузионным квазигетерогенным, но не полностью гетерогенным, поскольку процесс горения происходит уже не на границе фаз. Развитие такого горения осуществляется за счет теплового потока от факела пламени к поверхности материала, который обеспечивает дальнейшее испарение или разложение и поступление горючего в зону горения. В подобных ситуациях возникает смешанный случай, когда реакции горения частично протекают гетеро-генно - на поверхности конденсированной фазы, частично гомогенно - в объеме газовой смеси.
Примером гетерогенного горения является горение каменного и древесного угля. При сгорании этих веществ протекают реакции двоякого рода. Некоторые сорта каменного угля выделяют при нагревании летучие компоненты. Сгоранию таких углей предшествует их частичное термическое разложение с выделением газообразных углеводородов и водорода, сгорающих в газовой фазе. Кроме того, при сгорании чистого углерода может образовываться оксид углерода СО, догорающий в объеме. При достаточном избытке воздуха и высокой температуре поверхности угля объемные реакции протекают настолько близко от поверхности, что в определенном приближении дает основание считать такой процесс гетерогенным.
Примером действительно гетерогенного горения является горение тугоплавких нелетучих металлов. Эти процессы могут осложняться образованием окислов, покрывающих горящую поверхность и препятствующих контакту с кислородом. При большой разнице в физико-химических свойствах между металлом и его окислом в процессе горения окисная пленка растрескивается, и доступ кислорода в зону горения обеспечивается.
Глава 1. Основные понятия теории горения
1.3. Горение в движущемся газе
Для описания процессов горения используется термин «нормальная скорость пламени»*. Он характеризует скорость движения фронта пламени в неподвижной газовой смеси. Такое идеализированное состояние можно создать лишь в лабораторном эксперименте. В реальных условиях горения пламя всегда существует в движущихся потоках.
Поведение пламени в таких условиях подчиняется двум законам, установленным русским ученым В. А. Михельсоном.
Первый из них устанавливает, что составляющая скорости газового потока v по нормали к фронту пламени, распространяющегося по неподвижной смеси, равна нормальной скорости распространения пламени и, деленной на cos 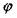
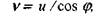 (1-1)
(1-1)
где 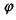 - угол между нормалью к поверхности пламени и направлением газового потока.
- угол между нормалью к поверхности пламени и направлением газового потока.
Величина v характеризует количество газа, сгорающего в единицу времени в косом пламени. Ее принято называть действительной скоростью горения в потоке. Действительная скорость во всех случаях равна или превышает нормальную.
Этот закон применим только к плоскому пламени. Обобщение его на реальные пламена с искривлением фронта пламени дает формулировку второго закона - закона площадей.
Предположим, что в газовом потоке, имеющем скорость v и поперечное сечение 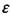 стационарно расположен искривленный фронт пламени с общей поверхностью S. В каждой точке фронта пламени пламя распространяется по нормали к его поверхности со скоростью и. Тогда объем горючей смеси, сгорающей в единицу времени
стационарно расположен искривленный фронт пламени с общей поверхностью S. В каждой точке фронта пламени пламя распространяется по нормали к его поверхности со скоростью и. Тогда объем горючей смеси, сгорающей в единицу времени 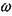 составит:
составит:
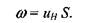 (1.2)
(1.2)
В соответствии с балансом исходного газа этот же объем равен:
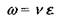 (1.3)
(1.3)
* Этот термин адекватен термину «нормальная скорость горения».
Корольченко А.Я. Процессы горения и взрыва
Приравнивая левые части (1.2) и (1.3) получаем:
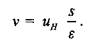
|
(1.4)
В системе отсчета, в которой фронт пламени перемещается по неподвижной газовой смеси, соотношение (1.4) означает, что пламя распространяется относительно газа со скоростью V. Формула (1.4) является математическим выражением закона площадей, из которого следует важный вывод: при искривлении фронта пламени скорость горения вырастает пропорционально увеличению его поверхности. Поэтому неоднородное движение газа всегда интенсифицирует горение.
1.4. Турбулентное горение
Из закона площадей следует, что турбулентность увеличивает скорость горения. На пожарах это выражается сильной интенсификацией процесса распространения пламени.
Различают (рис. 1.2) два вида турбулентного горения: горение однородной газовой смеси и микродиффузионное турбулентное горение.
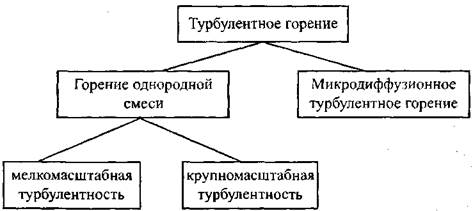
Рис. 1.2. Классификация турбулентного горения
При горении однородной смеси в режиме турбулентного горения возможны два случая: возникновение мелкомасштабной и крупномас-
Глава 1. Основные понятия теории горения
штабной турбулентности. Такое разделение производится в зависимости от соотношения масштаба турбулентности и толщины фронта пламени. При масштабе турбулентности меньшем толщины фронта пламени ее относят к мелкомасштабной, при большем - к крупномасштабной. Механизм действия мелкомасштабной турбулентности обусловлен интенсификацией процессов горения за счет ускорения процессов тепломассопере-носа в зоне пламени. При описании мелкомасштабной турбулентности в формулах для скорости распространения пламени коэффициенты диффузии и температуропроводности заменяются на коэффициент турбулентного обмена.
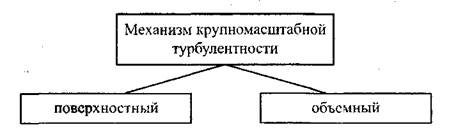
Наибольшие скорости горения наблюдаются при крупномасштабной турбулентности. В этом случае возможны два механизма ускорения горения: поверхностный и объемный.
|
Поверхностный механизм состоит в искривлении фронта пламени турбулентными пульсациями. В этом случае скорость горения возрастает пропорционально увеличению поверхности фронта. Однако это справедливо лишь для условий, когда химические превращения в пламени завершаются быстрее, чем успеет произойти турбулентное смешение. В этом случае, когда турбулентное смешение обгоняет химическую реакцию, зона реакции размывается турбулентными пульсациями. Такие процессы описываются закономерностями объемного турбулентного горения.
Время турбулентного смешения 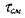 равно отношению масштаба
равно отношению масштаба
турбулентности 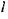 к пульсационной скорости
к пульсационной скорости 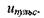 Поэтому ускорение
Поэтому ускорение
пламени за счет турбулентных пульсаций происходит по поверхностному механизму, если выполняется условие:
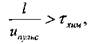
|
(1.5)
Корольченко А.Я. Процессы горения и взрыва
где 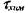 - время протекания химической реакции при температуре горе-
- время протекания химической реакции при температуре горе-
ния 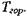
Если условие (1.5) не выполняется, то имеет место механизм объемного турбулентного горения.
Время химической реакции может быть выражено .через макроскопические величины: нормальную скорость пламени и толщину фронта пламени 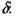
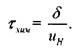 (1.6)
(1.6)
Тогда критерий поверхностного ускорения принимает вид:
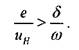 (1.7)
(1.7)
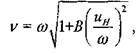
|
| (1.8) |
Для оценки скорости 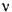 распространения турбулентного пламени при поверхностном ускорении К. И. Щелкиным предложена формула:
распространения турбулентного пламени при поверхностном ускорении К. И. Щелкиным предложена формула:
где В - слабо меняющееся число, не превышающее единицу. В пределе при сильной турбулентности турбулентная скорость пламени стремится к пульсационной скорости, т. е. В - к единице.
1.5. Особенности горения взрывчатых веществ
Взрывчатыми называются индивидуальные вещества или их смеси, способные под влиянием какого-либо внешнего воздействия (нагревания, удара, трения, взрыва другого взрывчатого вещества) к быстрому самораспространяющемуся химическому превращению с выделением большого количества тепла и образованием газов.
От обычных горючих веществ, горение которых происходит при взаимодействии с кислородом или другими внешними оксилителями, взрывчатые вещества, находясь в конденсированной (твердой или жидкой) фазе, содержат в себе все компоненты, участвующие в горении. Взрывчатыми веществами могут быть как индивидуальные химические соединения, так и механические смеси.
Большинство индивидуальных взрывчатых веществ относятся к нитросоединениям: тринитротолуол, тетрил, гексоген, октоген, нитрогли-
Глава 1. Основные понятия теории горения
церин, нитраты целлюлозы и др. Взрывчатыми свойствами обладают также хлораты, перхлораты, азиды, органические перекиси.
Молекулы органических нитросоединений содержат слабо связанный кислород в виде нитрогруппы - 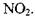 Таким образом, в одной молекуле содержатся и горючее, и окислитель. Их горение за счет внутримолекулярного окисления может начаться при незначительных внешних воздействиях.
Таким образом, в одной молекуле содержатся и горючее, и окислитель. Их горение за счет внутримолекулярного окисления может начаться при незначительных внешних воздействиях.
Значительную группу взрывчатых веществ составляют эндотермические соединения, молекулы которых не содержат кислорода. В этом случае источником энергии является не окисление, а прямой распад. К таким соединениям относятся азиды свинца, серебра и других металлов. К механическим смесям относятся смеси твердых у глее о держащих горючих с твердыми окислителями. Примером подобной смеси является черный порох.
1.6. Термодинамика сгорания
углеводородовоздушных смесей
Законы термодинамики позволяют вычислить необходимые для описания процессов горения параметры: коэффициент расширения продуктов сгорания при начальных условиях 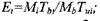 отношения теп-лоемкостей при постоянном давлении и постоянном объеме
отношения теп-лоемкостей при постоянном давлении и постоянном объеме 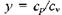 как хтя свежей смеси, так и для продуктов сгорания; максимальное давление взрыва ре; адиабатическую температуру продуктов сгорания в изобарических и изохорических условиях, состав продуктов сгорания
как хтя свежей смеси, так и для продуктов сгорания; максимальное давление взрыва ре; адиабатическую температуру продуктов сгорания в изобарических и изохорических условиях, состав продуктов сгорания
В настоящем разделе описан алгоритм расчета равновесного состояния продуктов сгорания C-H-0-N- содержащих горючих в воздухе в широком диапазоне начальных температур, давлений и концентраций, разработанный проф. В.В. Мольковым. Алгоритм основан на обобщении и систематизации термодинамических и математических методов с использованием наиболее точных данных по термодинамическим свойствам индивидуальных веществ.
Для повышения достоверности результатов в расчетах необходимо учитывать не только кислород и азот воздуха, но и другие входящие в его состав газы - 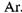 , Н20, С02. Увеличение числа компонентов продуктов сгорания до 19 (Н2, Н20, С02, N2, Аг, С-газ, Н, О, N, CO, CH4, HCN, 02,
, Н20, С02. Увеличение числа компонентов продуктов сгорания до 19 (Н2, Н20, С02, N2, Аг, С-газ, Н, О, N, CO, CH4, HCN, 02,
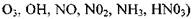 и проведение расчетов с учетом состава воз-
и проведение расчетов с учетом состава воз-
Корольченко А.Я. Процессы горения и взрыва
духа средней влажности 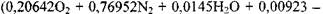
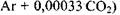 не усложняют вычислений на компьютере, использование которого позволяет существенно сократить время расчетов при одновременном повышении их точности в сравнении с приближенным подходом без использования компьютера.
не усложняют вычислений на компьютере, использование которого позволяет существенно сократить время расчетов при одновременном повышении их точности в сравнении с приближенным подходом без использования компьютера.
Брутто-реакция для сгорания горючего в воздухе средней влажности в расчете на моль свежей смеси может быть записана в виде
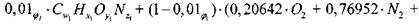
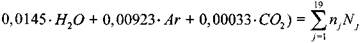 (1.9)
(1.9)
где  - объемная концентрация горючего в свежей смеси:
- объемная концентрация горючего в свежей смеси: 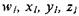 -
-
число атомов соответственно углерода, водорода, кислорода и азота в молекуле горючего; 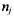 - число молей
- число молей 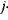 -го компонента продуктов сгорания;
-го компонента продуктов сгорания; 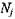
- 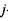 -й компонент продуктов сгорания.
-й компонент продуктов сгорания.
Суммарное число атомов в системе, вычисленное по составу свежей смеси, равно
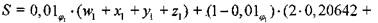
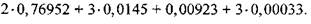 (1-10)
(1-10)
Отношения числа атомов соответственно углерода, водорода, азота и аргона к числу атомов кислорода являются константами для конкретной смеси и не зависят от термодинамического состояния замкнутой системы:
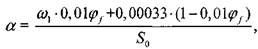 (1.11)
(1.11) 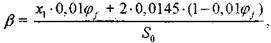 (1.12)
(1.12)
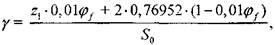 (1.13)
(1.13)
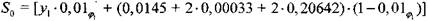 (1.14)
(1.14)
- число атомов кислорода в системе.
Глава 1. Основные понятия теории горения
Для адиабатического процесса горения в изобарических условиях закон сохранения энергии эквивалентен закону сохранения энтальпии замкнутой системы
Hi = Hj, (1.15)
где Н - энтальпия, а индексы 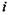 и j обозначают соответственно параметры свежей смеси и продуктов сгорания. Энтальпия моля свежей смеси
и j обозначают соответственно параметры свежей смеси и продуктов сгорания. Энтальпия моля свежей смеси
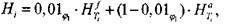 (1.16)
(1.16)
где 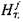 и
и 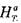 - энтальпия соответственно горючего и воздуха при на-
- энтальпия соответственно горючего и воздуха при на-
чальной температуре 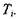 Зависимость энтальпии горючего и воздуха от начальной температуры в диапазоне от 250 до 500 К задается полиномом четвертой степени
Зависимость энтальпии горючего и воздуха от начальной температуры в диапазоне от 250 до 500 К задается полиномом четвертой степени
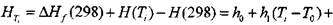
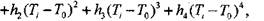 <1.17)
<1.17)
где 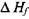 (298) - энтальпия образования вещества при температуре 298 К;
(298) - энтальпия образования вещества при температуре 298 К;
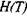 - энтальпия при температуре Т;
- энтальпия при температуре Т; 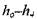 - численные коэффициенты,
- численные коэффициенты,
определяемые решением системы линейных уравнений, например, методом исключения Гаусса-Жордана; Т0 - некоторое произвольное постоянное значение температуры.
Энтальпия продуктов сгорания, полученных при сжигании моля свежей смеси
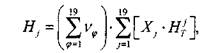
|
(1.18)
гдесумма в круглых скобках равна числу молей продуктов при сгорании одного моля свежей смеси; 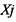 - мольная доля -го компонента продуктов сгорания;
- мольная доля -го компонента продуктов сгорания; 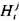 - энтальпия
- энтальпия 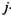 -го продукта
-го продукта 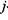 сгорания при темпера-
сгорания при темпера-
туре Т.
Значения энтальпий
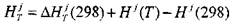 (1.19)
(1.19)
определяются по зависимости приведенной энергии Гиббса от температуры Ф(Т) в диапазоне температур от 500 до 6000 К. Известно, что
Корольченко А.Я. Процессы горения и взрыва
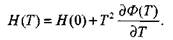
|
(1.20)
При горении в изохорических условиях, например при взрыве газа в бомбе постоянного объема, переход системы из исходного равновесного термодинамического состояния в конечное происходит с сохранением внутренней энергии
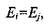 (1.21)
(1.21)
где на моль свежей смеси 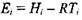 (универсальная газовая постоянная
(универсальная газовая постоянная
R - 8,31441 Дж/моль • К), а для продуктов сгорания
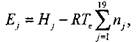
|
(1.22)
где Те - равновесная температура продуктов сгорания в бомбе.
Давление взрыва газовой смеси в замкнутой бомбе определяется по отношению уравнений состояния идеального газа для продуктов сгорания и свежей смеси
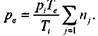 (1.23)
(1.23)
Для нахождения равновесного состава продуктов сгорания необходимо решить систему, включающую в себя 5 линейных (уравнения сохранения массы) и 14 нелинейных (уравнения химического равновесия) алгебраических уравнений.
Для изобарического процесса целесообразно записать уравнения сохранения массы через мольные доли продуктов сгорания 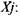
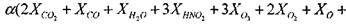
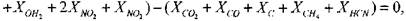 (1.24)
(1.24)
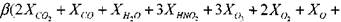
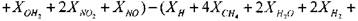 (1.25)
(1.25)
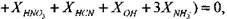
Глава 1. Основные понятия теории горения
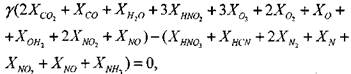
|
(1.26)
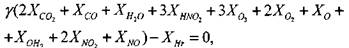
|
(1.27)
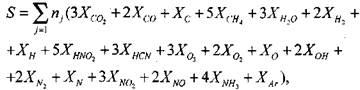
|
(1.28)
где значения 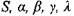 определены по параметрам свежей смеси в соот-
определены по параметрам свежей смеси в соот-
ветствии с формулами (1.10)-(1.14).
Сумма мольных долей по определению равна единице
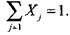 (1.29)
(1.29)
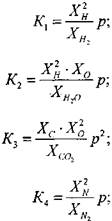
|
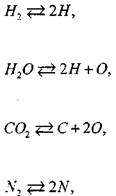
|
Число независимых уравнений химического равновесия равно разности числа компонентов продуктов сгорания и числа химических элементов в системе. В качестве независимых выбраны следующие четырнадцать реакций:
(1.30) (1.31) (1.32)
(1.33)
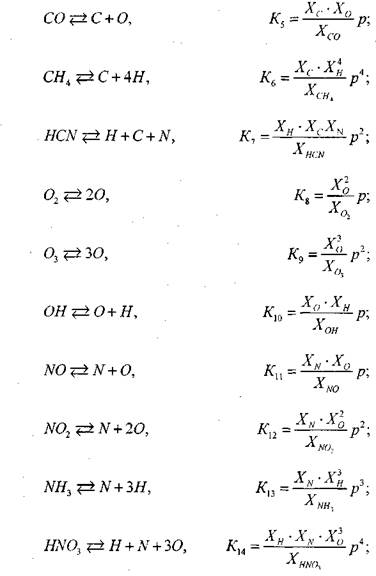
|
Корольченко А.Я. Процессы горения и взрыва
(1.34) (1.35) (1.36) (1.37) (1.38) (1.39) (1.40) (1.41) (1.42) (1.43)
где р - давление, при котором протекает реакция, атм. Зависимость констант химического равновесия 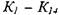 от температуры принимается по справочным данным для реакций диссоциации
от температуры принимается по справочным данным для реакций диссоциации
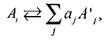
|
(1.43 а)
Глава 1. Основные понятия теории горения
где 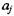 - стехиометрические коэффициенты, определяются из соотношения
- стехиометрические коэффициенты, определяются из соотношения
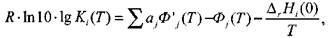
|
(1.44)
котором 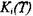 - константа равновесияреакции
- константа равновесияреакции 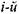 диссоциации (1.43 а)
диссоциации (1.43 а)
при температуре 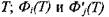 - приведенные энергии Гиббса соответ-
- приведенные энергии Гиббса соответ-
ственно реагентов 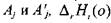 - тепловой эффект-ой
- тепловой эффект-ой 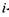 реакции (1.44)
реакции (1.44)
при абсолютном нуле температуры.
Показатели адиабат для свежей смеси и продуктов сгорания определяются с использованием уравнения Майера по формуле
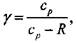
|
(1.45)
где у- показатель адиабаты; ср - мольная теплоемкость при постоянном давлении; R - универсальная газовая постоянная. Теплоемкость смеси идеальных газов вычисляется по формуле
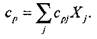
|
(1.46)
Для свежей смеси значения 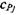 определяются дифференцированием выражения (1.17) для энтальпии газов исходной смеси (горючего и воздуха) по температуре
определяются дифференцированием выражения (1.17) для энтальпии газов исходной смеси (горючего и воздуха) по температуре 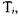 для продуктов сгорания - по выражениям, полученным в результате дифференцирования уравнения (1.19) по температуре Т.
для продуктов сгорания - по выражениям, полученным в результате дифференцирования уравнения (1.19) по температуре Т.
При расчетах процессов горения в постоянном объеме константу равновесия 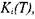 зависящую для идеального газа только от температуры,
зависящую для идеального газа только от температуры,
при которой рассчитывается равновесие, и не зависящую от давления, целесообразно записать не через мольные доли 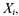 как это сделано при расчетах горения в изобарических условиях в уравнениях (1.30)-(1.43), а через количество молей п,. Тогда, например, для реакции (1.31) имеем
как это сделано при расчетах горения в изобарических условиях в уравнениях (1.30)-(1.43), а через количество молей п,. Тогда, например, для реакции (1.31) имеем
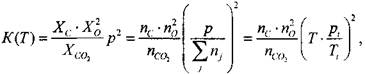
|
(1.47)
где Г-температура, при которой вычисляется константа равновесия; р, и Г, - начальные значения давления и температуры свежей смеси. При пе-
Корольченко А.Я. Процессы горения и взрыва
реходе от мольных долей к числу молей в изохорическом процессе в уравнениях сохранения массы (15)-(18) необходимо заменить значения 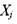 на соответствующие
на соответствующие 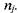 Уравнение (19) этом запишется в виде
Уравнение (19) этом запишется в виде
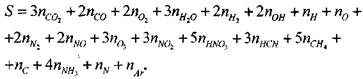 (1.48)
(1.48)
После умножения обеих частей уравнения (1.28) на можно вычислить сумму 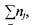 необходимую для вычисления давлениявзрыва
необходимую для вычисления давлениявзрыва 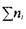 газовой смеси в бомбе постоянного объема по уравнению (1.22).
газовой смеси в бомбе постоянного объема по уравнению (1.22).
Опишем метод решения системы уравнений (1.15), (1.23)-(1.43), содержащей 21 неизвестную величину: 19 мольных долей продуктов сгорания 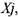 суммарное число молей продуктов при сгорании моля свежей смеси
суммарное число молей продуктов при сгорании моля свежей смеси 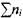 и энтальпию продуктов сгорания
и энтальпию продуктов сгорания 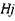 . В качестве независимых переменных выбраны мольные доли водорода, воды, диоксида углерода, азота и аргона
. В качестве независимых переменных выбраны мольные доли водорода, воды, диоксида углерода, азота и аргона 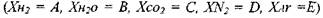 Мольные
Мольные
доли остальных 14 продуктов сгорания выражаются через константы равновесия и выбранные независимые переменные из уравнений (1.29)-(1.43). Далее перепишем уравнения (1.23)-(1.26) и (1.28) соответственно в виде
F(A,B, C,D,E) = 0,
G (А, В, С, D, Е) = 0,
H(A,B,C,D,.E) = 0, (1.49)
J (А, В, С, D, Е) = 0,
I (А, В, С, D, Е) = 0.
Линеаризовав систему уравнений (1.49) разложением в ряд Тейлора с точностью до членов, содержащих первые производные, получаем
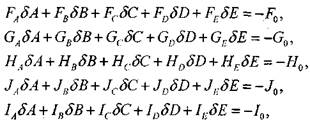 (1.50)
(1.50)
где 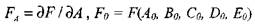 и т. д. (индекс 0 обозначает ис-
и т. д. (индекс 0 обозначает ис-
ходные значения величин). Система уравнений (1.50) содержит пять неизвестных - 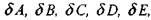 являющихся приращениями к исходным
являющихся приращениями к исходным
Глава 1. Основные понятия теории горения
вестных - 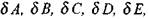 являющихся приращениями к исходным
являющихся приращениями к исходным
значениям мольных долей А, В, С, D, Е. Система может быть решена различными методами, например вычислением и делением друг на друга детерминантов соответствующих матриц системы уравнений (1.50) либо использованием метода исключения Гаусса-Жордана.
При предполагаемом значении равновесной температуры продуктов сгорания Т вычисляют значения констант равновесия 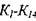 .. Затем определя-
.. Затем определя-
ют по исходным значениям независимых переменных А, В, С, D, Е значения остальных мольных, долей продуктов сгорания, а следовательно, и коэффициенты системы уравнений (1.50). Затем, решив эту систему уравнений, находят новые значения 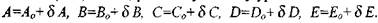
Итерационный процесс повторяют до тех пор, пока абсолютные значения отношений 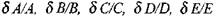 не станут меньше определенной величины, равной, например,
не станут меньше определенной величины, равной, например, 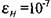 (при
(при 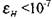 результаты расчетов практически не изменяются). Таким образом, определяют равновесный состав продуктов сгорания при предполагаемой температуре Т. По равновесному составу продуктов находят согласно уравнению (1.27) величину £и,-, что позволяет вычислять значения энтальпии Hj продуктов сгорания по формуле (1.18).
результаты расчетов практически не изменяются). Таким образом, определяют равновесный состав продуктов сгорания при предполагаемой температуре Т. По равновесному составу продуктов находят согласно уравнению (1.27) величину £и,-, что позволяет вычислять значения энтальпии Hj продуктов сгорания по формуле (1.18).
При горении в изохорических условиях порядок вычислений аналогичен описанному выше. Отличие, как уже отмечалось, заключается в том, что расчет проводится не для мольных долей, а для числа молей и вместо энтальпий вычисляют внутреннюю энергию свежей смеси и продуктов сгорания.
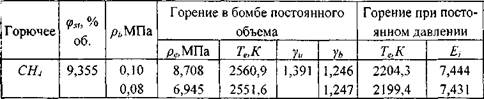
В табл. 1.1 приведены рассчитанные термодинамические параметры для стехиометрических смесей метана, пропана, гексана, гептана, ацетона, изопропилового спирта и бензола с воздухом.
Таблица 1.1. Максимальное адиабатическое давление взрыва в замкнутом сосуде 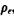 , температура продуктов сгорания
, температура продуктов сгорания 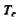 , показатели адиабат свежей смеси
, показатели адиабат свежей смеси 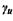 и продуктов сгорания
и продуктов сгорания 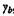 коэффициент расширения продуктов сгорания при начальных условиях Ei для стехиометрических углеводородных смесей при
коэффициент расширения продуктов сгорания при начальных условиях Ei для стехиометрических углеводородных смесей при
начальной температуре 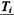 = 298,15 К
= 298,15 К
Корольченко А.Я. Процессы горения и взрыва
| 0,06 0,04 | 5,188 3,439 | 2539,6 2521,9 | 1,247 1,248 | 2192,7 2183,2 | 7,412 7.385 | |||
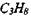
| 3,964 | 0,10 0,08 0,06 0,04 | 9,228 7,358 5,494 3,640 | 2604,4 2594,1 2580,5 2561,2 | 1,365 | 1,247 1,248 1,248 1,249 | 2245,2 2239,4 2231,7 2220,7 | 7,897 7,880 7,857 7,825 |
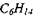
| 2,126 | 0,10 0,08 0,06 0,04 | 9,378 7,478 5,583 3,699 | 2611,6 2601,2 2587,3 2567,8 | 1,360 | 1,248 1,248 1,249 1,249 | 2251,7 2245,8 2237,9 2226,7 | 8,025 8,008 7,984 7,951 |
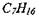
| 1,842 | 0,10 0,08 0,06 0,04 | 9,403 7,498 5,598 3,708 | 2613,0 2602,6 2588,7 2569,1 | 1,359 | 1,248 1,248 1,249 1,249 | 2253,0 2247,1 2239,1 2227,9 | 8,047 8,029 8,005 7,972 |
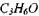
| 4,907 | 0,10 0,08 0,06 0,04 | 9,282 7,401 5,527 3,661 | 2594,2 2583,7 2570,4 2550,9 | 1,357 | 1,245 1,245 1,246 1,246 | 2242,1 2236,2 2228,2 2216,9 | 7,962 7,944 7,921 7,888 |
| 4,386 | 0,10 0,08 0,06 0,04 | 9,344 7,451 5,565 3,688 | 2574 3 2564,4 2551,8 2533,2 | 1,361 | 1,244 1,245 1,245 1,246 | 2219,7 2214,3 2206,9 2196,5 | 7,999 7,983 7,961 7,929 |
| 2,679 | 0,10 0,08 0,06 0,04 | 9,299 7,411 5,532 3,662 | 2678,2 2666,0 2650,6 2628,2 | 1,377 | 1,251 1,251 1,252 1,252 | 2321,1 2313,7 2304,2 2290,4 | 7,990 7,969 7,942 7,902 |
Стехиометрическая концентрация горючего при сгорании в воздухе средней влажности и в сухом воздухе определяются соответственно по формулам:
(1.51)
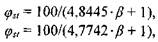 (1.52)
(1.52)
где 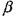 - стехиометрический коэффициент кислорода, равный числу молей кислорода, приходящихся на 1 моль горючего вещества при его полном сгорании.
- стехиометрический коэффициент кислорода, равный числу молей кислорода, приходящихся на 1 моль горючего вещества при его полном сгорании.
Глава 1. Основные понятия теории горения
На рис. 1.3 в качестве примера показано рассчитанное изменение температуры горения и мольных долей основных компонентов продуктов сгорания в зависимости от объемной концентрации горючего для гекса-но-воздушной смеси.
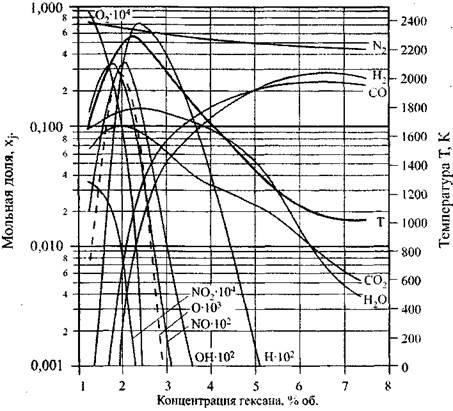
Рис. 1.3. Зависимость состава и температуры продуктов сгорания
гексано-воздушной смеси при давлении 0,101 МПа и начальной температуре
298,15 К от концентрации гексана
Дата добавления: 2015-09-29; просмотров: 4751;
