Метод поднесения под знак дифференциала
Для вычисления интеграла используют определение дифференциала:
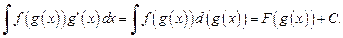
Согласно этому методу не делают явно замену переменной, подразумевая, что g(x) играет роль новой независимой переменной.
При использовании метода поднесения под знак дифференциала, метода замены переменной, метода подстановки удобно использовать простейшие преобразования дифференциала:
1)  (b – произвольная постоянная величина);
(b – произвольная постоянная величина);
2) 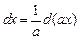 (постоянная
(постоянная  );
);
3) 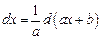 (постоянная
(постоянная 
Пример 1. Найти неопределенный интеграл:
1)  2)
2) 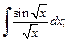 3)
3) 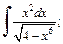 4)
4) 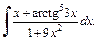
Решение.1) 1-й способ. Используем метод замены переменной. Положим  Тогда
Тогда 
 Имеем:
Имеем:


Для вычисления интеграла использовали формулу (19.3) таблицы неопределенных интегралов.
2-й способ. Используем метод поднесения под знак дифференциала. Представим данный интеграл в следующем виде:
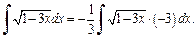
Учитывая, что 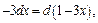 по формуле (19.3) таблицы неопределенных интегралов получаем:
по формуле (19.3) таблицы неопределенных интегралов получаем:


2) Поскольку 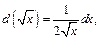 то
то  Поднесение под дифференциал приводит далее к интегралу
Поднесение под дифференциал приводит далее к интегралу 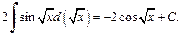
Для вычисления интеграла использовали формулу (19.8) таблицы неопределенных интегралов.
3) Очевидно, что  Значит,
Значит,

Применяя формулу (19.14) таблицы интегралов, получаем ответ: 
4) Используя второе свойство неопределенного интеграла, представим заданный интеграл в виде суммы двух интегралов:

Вычислим полученные интегралы отдельно. Так как  то, используя далее формулу (19.5) таблицы интегралов, получаем:
то, используя далее формулу (19.5) таблицы интегралов, получаем:

Так как 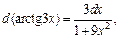 то по формуле (19.3) таблицы интегралов имеем:
то по формуле (19.3) таблицы интегралов имеем:
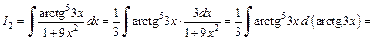

Подставив найденные значения интегралов I1(x) и I2(x) в первоначальный интеграл, приходим к ответу: 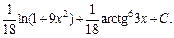
Пример 2. Методом подстановки найти интеграл:
1) 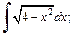 2)
2) 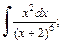 3)
3) 
Решение.1) Используем метод подстановки. Положим 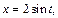 тогда
тогда 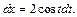

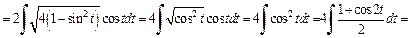


Для вычисления последних интегралов использовали формулы (19.4) и (19.9) таблицы интегралов. Выразим переменную t через переменную x.

 Тогда
Тогда 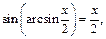
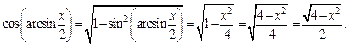
Получаем ответ: 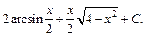
2) Применим подстановку 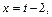 тогда
тогда 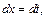
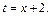 Таким образом,
Таким образом,
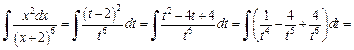


Для вычисления интеграла использовали формулу (19.3) таблицы интегралов.
3) Применим подстановку 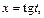 тогда
тогда 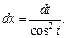 Получаем:
Получаем:
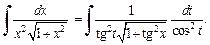
Используя тригонометрическое тождество 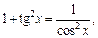 имеем:
имеем:
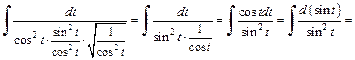
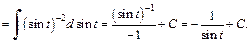
Вернемся к переменной x, для чего выразим t через x из подстановки 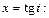
 Тогда
Тогда
 Таким образом,
Таким образом,
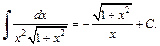
Интегрирование некоторых выражений,
содержащих квадратный трехчлен 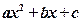
Рассмотрим некоторые виды интегралов, содержащих квадратный трехчлен в подынтегральном выражении, и способы их вычисления. Всюду далее считаем 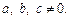
Для вычисления интеграла вида
 (19.17)
(19.17)
выделим полный квадрат в квадратном трехчлене:

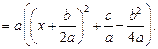
Сделаем замену переменной 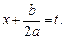 Тогда интеграл (19.17), в зависимости от знака выражения
Тогда интеграл (19.17), в зависимости от знака выражения 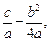 сводится к одному из интегралов
сводится к одному из интегралов 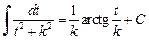 или
или 
Вместо замены переменной (после выделения полного квадрата) можно использовать также метод поднесения под знак дифференциала.
Интеграл вида
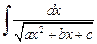 (19.18)
(19.18)
также вычисляется выделением полного квадрата в квадратном трехчлене. Он сводится к интегралу
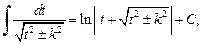 если
если 
или к интегралу
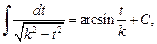 если
если 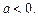
Рассмотрим интеграл вида
 где
где 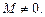 (19.19)
(19.19)
В числителе подынтегральной функции выделяем производную  квадратного трехчлена, записанного в знаменателе. Тогда интеграл (19.19) можно представить в виде суммы двух интегралов, один из которых сводится к интегралу
квадратного трехчлена, записанного в знаменателе. Тогда интеграл (19.19) можно представить в виде суммы двух интегралов, один из которых сводится к интегралу  а второй вычисляем как интеграл вида (19.17).
а второй вычисляем как интеграл вида (19.17).
Интеграл вида 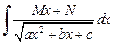 сводится к сумме интегралов
сводится к сумме интегралов 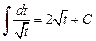 и вида (19.18).
и вида (19.18).
Интегралы вида 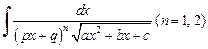 сводятся к рассмотренным выше интегралам с помощью подстановки
сводятся к рассмотренным выше интегралам с помощью подстановки 
Интеграл вида 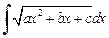 после выделения полного квадрата и замены
после выделения полного квадрата и замены 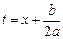 сводится к одному из интегралов
сводится к одному из интегралов 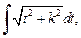
 или
или  которые могут быть вычислены методом интегрирования по частям (см. п. 19.4.) или с помощью тригонометрических подстановок (см. п. 19.7.), или как интеграл от дифференциального бинома (см. п. 19.8).
которые могут быть вычислены методом интегрирования по частям (см. п. 19.4.) или с помощью тригонометрических подстановок (см. п. 19.7.), или как интеграл от дифференциального бинома (см. п. 19.8).
Пример 1. Найти неопределенный интеграл:
1) 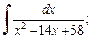 2)
2) 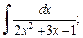
3) 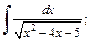 4)
4) 
Решение: 1) Выделим в знаменателе дроби полный квадрат:
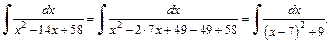
Используем метод поднесения под знак дифференциала. Интеграл примет вид:

Для вычисления последнего интеграла использовали формулу (19.13) таблицы интегралов.
2) Вынесем в знаменателе подынтегрального выражения множитель 2 за скобки и выделим полный квадрат, получим:

Заменим 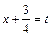 и
и  Интеграл примет вид:
Интеграл примет вид:
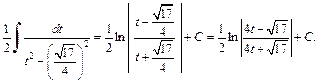
Для вычисления последнего интеграла использовали формулу (19.15) таблицы интегралов. Возвращаясь к переменной x, имеем:
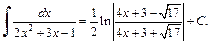
3) Выделив в подкоренном выражении полный квадрат, получаем:

Используя метод поднесения под знак дифференциала и формулу (19.16) таблицы интегралов, имеем:

4) Выделим в подкоренном выражении полный квадрат:

Применив метод поднесения под знак дифференциала и формулу (19.14) таблицы интегралов, получаем:
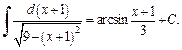
Пример 2. Найти неопределенный интеграл:
1) 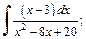 2)
2) 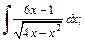 3)
3) 
Решение:1) Найдем производную квадратного трехчлена, записанного в знаменателе дроби, 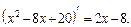
Выделим производную знаменателя в числителе дроби:
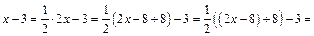

Тогда 
Используя второе свойство неопределенного интеграла, представим данный интеграл в виде суммы двух интегралов
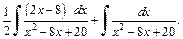
Выделим в знаменателе второго интеграла полный квадрат:

Для вычисления полученных интегралов используем метод поднесения под знак дифференциала и формулы (19.5) и (19.13) таблицы интегралов:


2) Выделим в подкоренном выражении полный квадрат:

Заменив 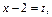

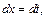 получим:
получим:
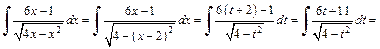
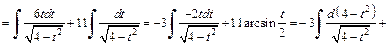

Для вычисления суммы интегралов использовали метод поднесения под знак дифференциала и формулы (19.3) и (19.14) таблицы интегралов.
3) Найдем производную квадратного трехчлена
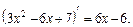
Выделим ее в числителе дроби, чтобы получить дифференциал знаменателя:
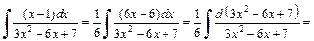
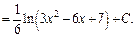
Для вычисления интеграла использовали метод поднесения под знак дифференциала и формулу (19.5) таблицы интегралов.
Пример 3. Найти неопределенный интеграл 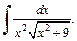
Решение:Применим подстановку 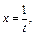 тогда
тогда  Получаем:
Получаем:

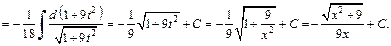
Дата добавления: 2015-09-29; просмотров: 1297;
