Однократное измерение углов.
При выполнении этого задания проводятся однократные измерения углов треугольника из набора принадлежностей, оцениваются погрешности измерения и результат представляется в виде: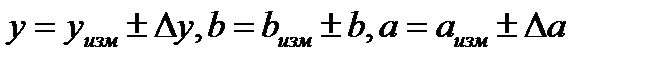 
, причем очевидно, что 
.
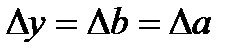2. Многократные измерения углов.
Погрешности величин у, b, а находятся по формуле расчета погрешностей прямых измерений:
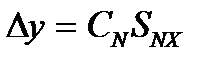. (1.26)
И в первом, и во втором случае можно проверить результат, используя формулу 
. При этом погрешность суммы углов отличается от погрешности измерения отдельного угла и вычисляется по формуле
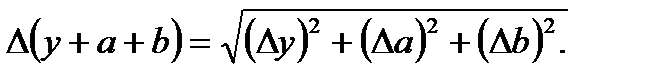(1.27)
Задание 4. Измерение времени секундомером.
Для измерения времени применяются секундомеры. Механические секундомеры имеют цену деления 0,1 и 0,2 с.
Основная погрешность этих секундомеров равна цене деления, а погрешность отсчета зависит от быстроты реакции на включение и остановку секундомера. Установлено, что неточности пуска и остановки дают погрешность порядка 0,3 с. Таким образом, при работе с секундомером с ценой деления 0,2 с погрешность может достигать 0,5 с.
Применяются электронные секундомеры с ценой деления 0,01 и 0,001 с. Их целесообразно использовать вместе с устройствами, обеспечивающими совпадение пуска и остановки с началом и концом процесса, длительность которого определяется.
Пример 6. По индикатору электронного секундомера с ценой деления 0,01 с зарегистрировано некоторое время 
. Результат измерения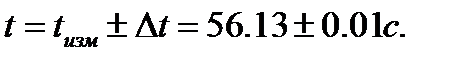 
Методика измерения интервалов времени и обработки результатов при однократных и повторных измерениях та же, что и в предыдущих заданиях по измерению линейных размеров и углов.
Задание 5. Измерение температуры термометром.
Термометр представляет собой капиллярную трубку из стекла, которая заполнена жидкостью, обычно ртутью или подкрашенным спиртом. Капиллярная трубка помещена в корпус из стекла, в котором также закреплена измерительная шкала. Погрешность измерения температуры термометрами различных типов регламентируется ГОСТ 400-80 и имеет, в большинстве случаев, величину, равную цене деления.
Методика измерения температуры и обработки результатов при однократных и многократных измерениях та же, что и в предыдущих заданиях.
Ускорение свободного падения
Гравитационное взаимодействие лежит в основе многих механических явлений. Оно возникает между любыми видами материи и является одним из фундаментальных взаимодействий. Гравитационное взаимодействие осуществляется посредством гравитационного поля. Всякое тело изменяет свойства окружающего его пространства, создавая в нем гравитационное поле. Это поле проявляет себя в том, что на помещенное в него другое тело действует сила.
| Рис. 2.1. Иллюстрация закона всемирного тяготения |
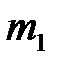и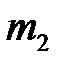 
, обратно пропорциональна квадрату расстояния 
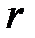между ними (рис.2.1).Силы направлены по прямой, соединяющей материальные точки, и в векторном виде записываются в следующем виде:
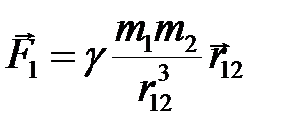
(2.1)
где 
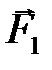и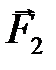 
– силы, действующие на соответствующие материальные точки, 
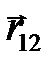– радиус-вектор, направленный от первой точки ко второй, 
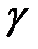– гравитационная постоянная 
.
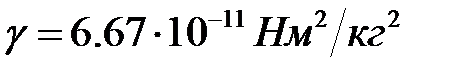Формулы (2.1) справедливы для материальных точек, то есть тел, размерами которых можно пренебречь по сравнению с расстоянием между ними, а так же в случае тел сферической формы (однородные шары, шаровые оболочки), размерами которых пренебречь нельзя, при этом под 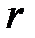следует понимать расстояние между центрами тел. Во всех остальных случаях формулы (2.1) неприменимы.
Согласно формуле (2.1) на всякое тело, находящееся вблизи поверхности Земли действует сила 
, где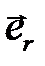 
– единичный вектор, направленный от центра Земли к телу. При 
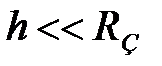, гравитационное поле Земли можно считать однородным и силу можно представить в ви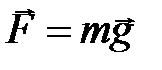де 
, где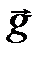 
– вектор ускорения свободного падения, направленный к центру Земли. Для среднего значения радиуса Земли 
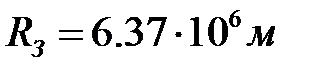его величина равна 
.
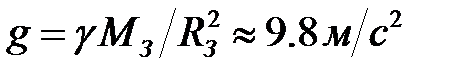Получим кинематические уравнения для материальной точки, движущейся с постоянным вектором ускорения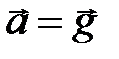 
, то есть в поле однородной силы тяжести.
По определению вектор ускорения материальной точки есть первая производная по времени от вектора скорости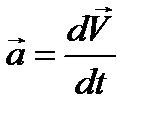 
, отсюда
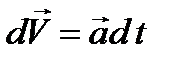. (2.2)
Проинтегрируем последнее уравнение с учётом, что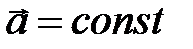 
:
,
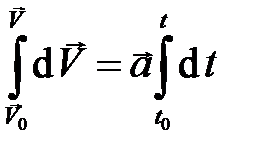отсюда
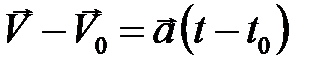, (2.3)
где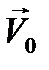 
, 
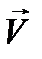– скорости материальной точки в начальный момент времени 
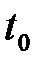и в некоторый последующий момент времени 
. Положив 
, получаем кинематическое уравнение для вектора скорости
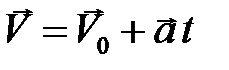(2.4)
Используя определение вектора скорости материальной точки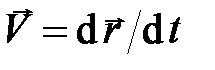 
, преобразуем уравнение (2.4) к виду
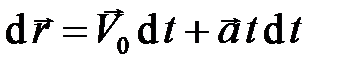. (2.5)
Проинтегрируем уравнение (2.5)
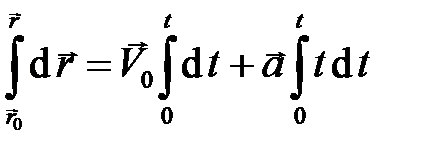, (2.6)
где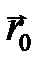 
и 
– радиус-векторы точки в моменты времени 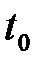и , соответственно. Из (2.6) получим
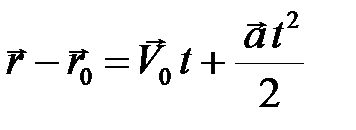. (2.7)
В проекциях на ось OX декартовой системы координат кинематические уравнения (2.4) и (2.7) имеют вид
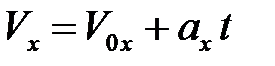и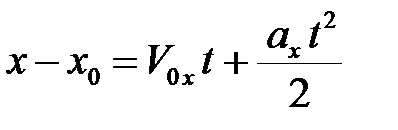 
, (2.8)
где 
, 
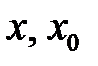– проекции соответствующих векторов на ось OX. Уравнения (2.4) и (2.7) в проекциях на оси OY и OZ имеют аналогичный вид.
Получим из (2.8) кинематические уравнения для тела, падающего с некоторой высоты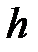 
с нулевой начальной скоростью. Начало отсчёта оси OY свяжем с уровнем, относительно которого отсчитывается высота 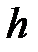, ось направим вертикально вверх. Представим вектора 
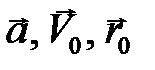, в координатной записи 
, 
, 
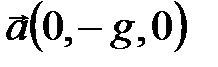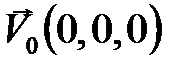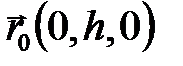. Так как проекции векторов на оси OX, OZ равны нулю, то получаем уравнения только в проекциях на ось OY:
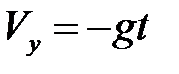и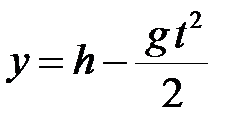 
. (2.9)
Из (2.9) следует формула связи высоты со временем, за которое совершается падение тела. Так как тело упало, то 
, отсюда
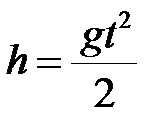. (2.10)
Дата добавления: 2015-09-25; просмотров: 616;