Лабораторная установка и проведение эксперимента.

Математический маятник представляет собой груз 1, подвешенный на длинной тонкой нити 2 (рис. 4.4). За длину маятника принимается расстояние от подвижной точки подвеса до центра масс груза. Свободный конец нити зажат в подвесе 2, закреплённом на зажиме 3 штатива 4. Время качаний определяется секундомером с помощью оптических датчиков, а угол отклонения – по специальной линейке 5.

Задание 1. Изучение зависимости периода малых колебаний от амплитуды.

Рис. 4.4. Общий вид установки

Маятник откланяется от положения равновесия на небольшой угол и без толчка отпускается. Определяется время, в течение которого маятник сделает n полных колебаний, за одно полное колебание шарик проходит путь, равный четырём амплитудам. Изменяется начальное отклонение шарика и определяется время колебаний.

Обработка результатов и расчёт погрешностей

1. Погрешности периода колебаний определить по методике расчёта погрешностей прямых многократных измерений, задавая доверительную вероятность 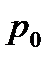и коэффициент Стьюдента.

2. При проверке независимости периода колебаний от амплитуды сравниваются периоды для различных амплитуд и находится такая величина 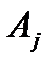, при которой 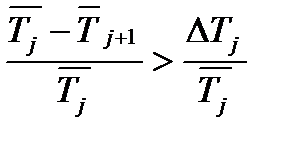. Это означает, что при амплитуде колебаний 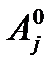, большей 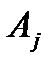, период зависит от амплитуды.

Задание 2. Изучение зависимости периода малых колебаний от длины маятника.

Изменяется длина маятника l и определяется период колебания. При этом масса маятника не изменяется, а амплитуда выбирается такой, при которой период не зависит от амплитуды. Для каждого значения длины маятника определяется время отклонений.

Обработка результатов и расчёт погрешностей

При обработке данных проверяется соотношение:

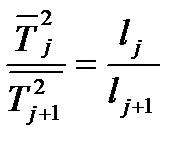(4.7)

Точность выполнения этого соотношения можно определить следующим образом:

1. Вычислить систематическую погрешность величины 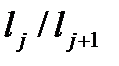по формуле

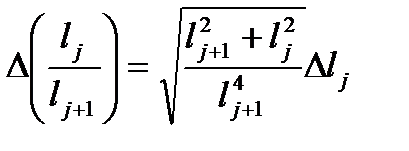, (4.8)

где 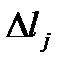− систематическая погрешность определения длины по линейке.

2. Погрешность косвенных повторных измерений величины 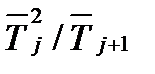вычислить по формуле

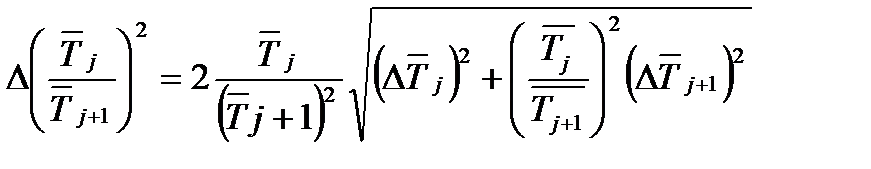. (4.9)

3. Случайные погрешности величин и рассчитать по методике расчёта погрешностей прямых измерений, задавая доверительную вероятность 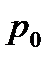и коэффициент Стьюдента.

4. Результаты расчётов проверить сравнением пар экспериментальных данных с учётом рассчитанных погрешностей.

Задание 3. Изучение зависимости периода малых колебаний от массы маятника.

Исследуется зависимость периода колебаний от массы маятника. Для этого изменяется масса маятника и остается неизменной его длина. Определяется период колебаний, и результаты опытов заносятся в таблицу.

Обработка результатов и расчёт погрешностей

1. Обработку результатов таблицы провести по п. 1 задания 1.

2. Сравнить периоды колебаний для различных масс груза и показать независимость периода от массы. При этом должно выполняться равенство

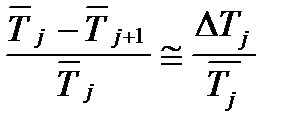. (4.10)

Задание 4. Измерение ускорения свободного падения. Используются результаты, полученные в задании 1, 2 или 3.

Обработка результатов и расчёт погрешностей.

1. Ускорение свободного падения рассчитать по зависимости, следующей из (4.3):

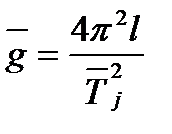, (4.11)

где время 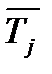выбирают из таблиц.

2. Погрешность случайных косвенных измерений величины g рассчитать по формуле

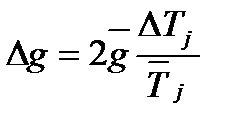, (4.12)

где величины 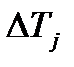, 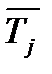взяты по данным таблиц.

3. Погрешность приборных косвенных измерений величины g рассчитать по формуле

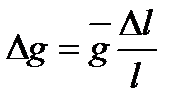. (4.13)

4. Полученную погрешность вычислить по формуле

. (4.14)

5. Результаты представить в виде: .

Задание 5. Изучение больших колебаний математического маятника.

При фиксированной массе груза и длине маятника измерить зависимость периода колебаний от угла отклонения маятника 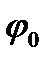в пределах до 30− 35 градусов через пять градусов. Для каждого отклонения маятника измерения провести несколько раз и заполнить таблицу.

Обработка результатов и расчёт погрешностей.

1. Погрешности периода колебаний 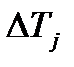определить по методике расчёта погрешностей прямых многократных измерений, задавая доверительную вероятность р₀ и коэффициент Стьюдента.

2. Построить зависимость нормированного теоретическим значением (4.3) периода колебаний маятника от угла отклонения 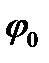, указав на графике нормированные доверительные интервалы по вертикальной оси координат. При этом в качестве 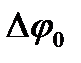по горизонтальной оси выбирается систематическая погрешность, равная половине деления шкалы, по которой измеряется первоначальное отклонение маятника.

3. На том же графике для данной длины маятника по формуле (4.5) построить нормированную теоретическую зависимость периода колебаний от угла первоначального отклонения маятника.

4. На том же графике для данной длины маятника по формуле (4.6) построить приближённую нормированную теоретическую зависимость периода колебаний от угла первоначального отклонения маятника.

5. Сравнить графики и найти величину отклонения, при которой выполняется приближение малых колебаний. Сравнить её с величиной 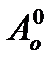, определённой в задании 1.

УПРУГИЙ УДАР

Удар – совокупность явлений, возникающих при кратковременном приложении к телу внешних сил, например, при взаимодействии с другим движущимся относительно него телом, связанных со значительным изменением его скорости за очень короткий промежуток времени.

Абсолютно неупругим называют такой удар, после которого скорости обоих соударяющихся тел оказываются одинаковыми.

Абсолютно неупругий удар характеризуется тем, что потенциальной энергии деформации не возникает – кинетическая энергия тел полностью или частично превращается во внутреннюю энергию. При абсолютно неупругом ударе выполняется лишь закон сохранения импульса и имеет место закон сохранения суммарной энергии различных видов – механической и внутренней.

Рис. 5.1. Упругое соударение шаров

m₁

m₂

m₁

m₂

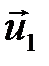
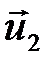
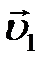
x

Абсолютно упругим называется такой удар, при котором механическая энергия тел не переходит в другие, немеханические, виды энергии. Потенциальная энергия упругой деформации вновь переходит в кинетическую энергию, и тела разлетаются со скоростями, величина которых определяется двумя условиями – сохранением полной энергии и сохранением полного импульса системы тел. Рассмотрим центральный абсолютно упругий удар двух шаров.

Удар называется центральным, если шары до удара движутся вдоль прямой, проходящей через их центры.

Пусть шары массам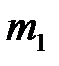и и 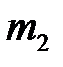движутся до соударения со скоростям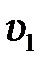и и 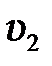, а после соударения со скоростями и 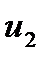(рис. 5.1). Согласно закону сохранения импульса

.

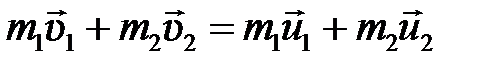Выберем ось x в направлении движения шаров, тогда в проекции на эту ось закон сохранения импульса принимает вид

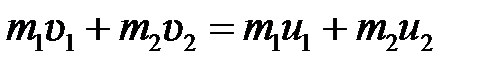. (5.1)

На основании закона сохранения энергии имеем

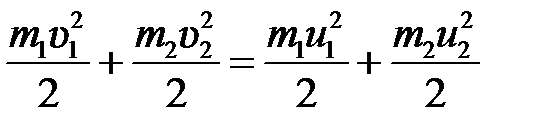. (5.2)

Сгруппировав слагаемые с одинаковыми индексами, перепишем эти равенства в виде

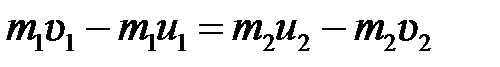, (5.3)

. (5.4)

Поделив (5.4) на (5.3), получим

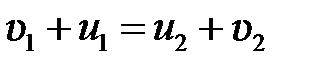(5.5)

или

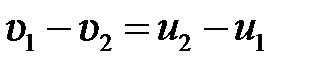. (5.6)

Таким образом, при абсолютно упругом ударе относительная скорость шаров остается неизменной величиной.

Решая совместно уравнения (5.5) и (5.3), получим

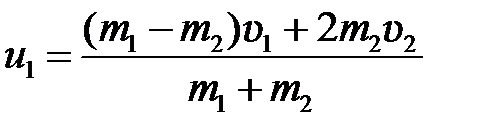, (5.7)

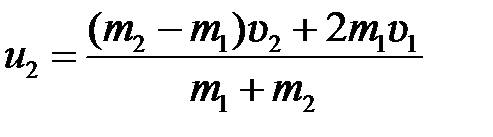. (5.8)

Рассмотрим два частных случая.

1. Сумма импульсов обоих шаров до ударов равна нулю, то есть

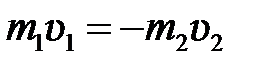, (5.9)

тогда , ,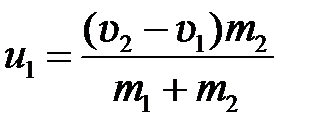

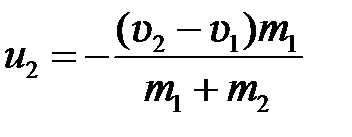отсюда, применяя (5.9), находим: 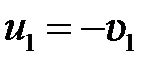, , 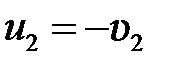то есть скорости обоих шаров при ударе только изменяют свой знак.

2. Один шар до удара покоится 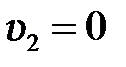. Тогда

, .

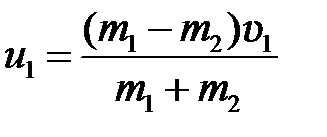После удара второй шар двинется в ту же сторону, куда двигался первый до удара. Скорость 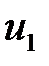и поведение первого шара зависит от соотношения масс шаров.

а) Если 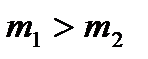, то первый шар продолжает двигаться в том же направлении, что и до удара, но с меньшей скоростью. Скорость второго шара после удара больше, чем скорость первого до удара.

б) Если 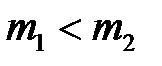, то направление движения первого шара при ударе изменяется – шар отскакивает обратно. Второй шар движется в ту сторону, в которую двигался первый до удара, но с меньшей скоростью.

в) Массы шаров одинаковы 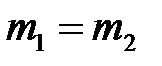, тогда 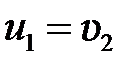, , 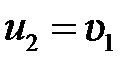то есть шары при ударе обмениваются скоростями. В случае абсолютно неупругого удара:

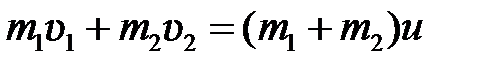, (5.10)

где 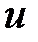– одинаковая для обоих шаров скорость после удара.

Из (5.10) следует, что 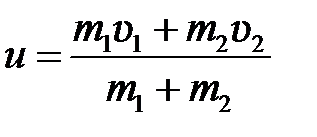. (5.11)

В частном случае, когда массы шаров равны, .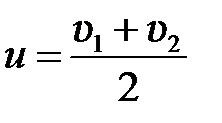

В случае нецентрального удара можно разложить скорости шаров на составляющие 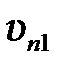и 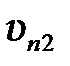в направлении линии центров 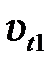и и 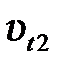в перпендикулярном направлении, а затем написать два уравнения, выражающие закон сохранения импульса для соответствующих составляющих:

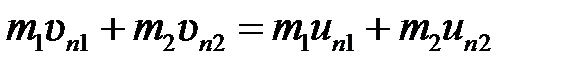, (5.12)

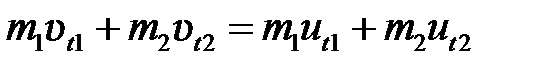. (5.13)

Так как , то закон сохранения энергии после сокращения на множитель ½ можно написать в виде

. (5.14)

Для четырех неизвестных компонент скорост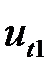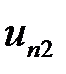и , , и 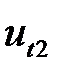получили только три уравнения. Но, поскольку мы сделали предположение, что энергия при ударе сохраняется, мы должны считать, что силы трения отсутствуют, то есть шары абсолютно гладкие. Из этого следует, что при ударе не могут измениться тангенциальные составляющие скоростей, так как для этого нужны тангенциальные силы, которые между абсолютно гладкими шарами возникнуть не могут. Поэтому вместо (5.13) можно записать

.

Соответствующие слагаемые в (5.14) сократятся, и для нормальных составляющих мы получим два уравнения:

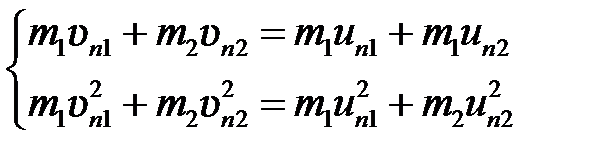. (5.15)

Эти уравнения совершенно аналогичны тем, которые были получены для центрального удара. Таким образом, при нецентральном абсолютно упругом ударе гладких шаров нормальные составляющие скоростей ведут себя так же, как при центральном ударе; тангенциальные же составляющие не изменяются.

Рис. 5.2. Соударение шаров

В случае не абсолютно упругого удара часть кинетической энергии шаров при соударении переходит в энергию остаточной деформации. Тогда . Отсюда можно получить, что 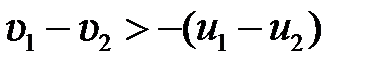, то есть при неупругом ударе относительная скорость их меняет свое направление на противоположное, уменьшаясь в то же время по абсолютной величине .

Неупругий удар сопровождается остаточной деформацией. Если пренебречь всякого рода сопротивлениями, закон сохранения энергии для удара двух одинаковых шаров запишется так

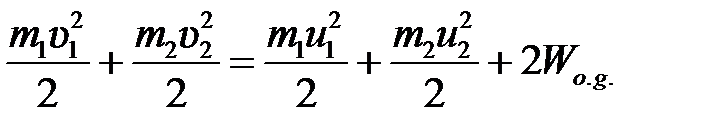, (5.16)

где – энергия остаточной деформации одного шара, относящаяся к одному соударению.

Экспериментальная установка и методика измерений

Схема лабораторной установки показана на рис. 5.3. К штативу 3 на бифилярных подвесах 4 и 5 прикреплены два шара 1 и 2. Бифилярный подвес используется для исключения вращения шаров. Шарики подвешены так, что их центры находятся на одном уровне, а сами шарики соприкасаются.

На столе под шариками в плоскости их колебания размещена линейка 6 (рис. 5.3).

Рис. 5.3. Схема установки

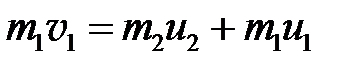Отведем один из шаров (например, большой) на некоторый угол θ (рис. 5,4) и отпустим без начальной скорости. Отклоненный шар будет двигаться вниз, разгоняясь, при этом его потенциальная энергия будет переходить в кинетическую. Пусть столкновение со вторым шаром происходит в тот момент, когда подвес первого шара становится вертикально. Если удар происходит достаточно быстро, так, что нити во время удара не успевают отклониться на заметный угол, то в направлении горизонтальной оси x не возникает внешних сил и выполняется закон сохранения импульса в проекции на эту ось

. (5.17)

По закону сохранения механической энергии (рис. 5.3)

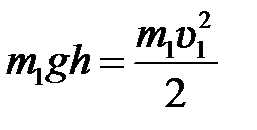, (5.18)

Рис. 5.4. Соударение шаров

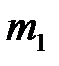где – масса шара, 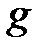– ускорение свободного падения, 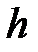– высота шара в отведенном положении относительно нижней точки траектории, 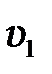– скорость первого шара в нижней точке перед соударением со вторым. Из рис. 5.4. видно, что 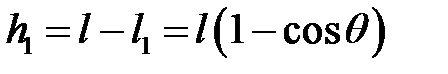, где – расстояние от точки подвеса до центра тяжести шара.

При достаточно малых отклонениях (≤ 5°)

.

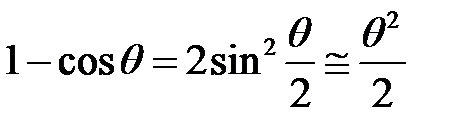Тогда с учетом приближенного равенства 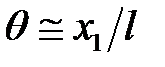, где x₁ – горизонтальное смещение шара, можно записать

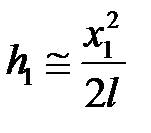. (5.19)

Из соотношений (5.18) и (5.19) получаем

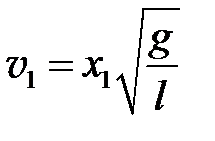. (5.20)

После удара оба шарика отклонятся от положения равновесия на расстояния 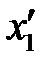и 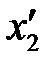и приобретут скорости u₁ и u₂:

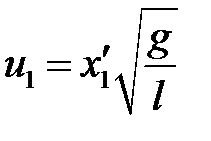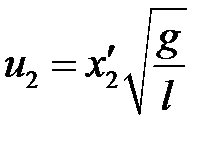, . (5.21)

Подставляя эти соотношения в закон сохранения импульса (5.17), после несложных преобразований получаем

(5.22)

Задание 1. Проверка соотношения (5.22).

Экспериментально проводится в следующей последовательности: большой шарик отклоняется из положения равновесия на фиксированную величину x₁, и после соударения по шкалам визуально определяются отклонения шаров 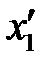и 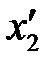. Опыт повторяют 5–7 раз.

Если в эксперименте отклоняется шарик меньшей массы, то при ударе о шар большей массы он отскакивает в противоположную сторону.

В этом случае , , .

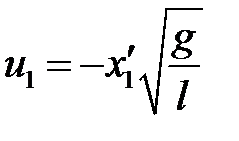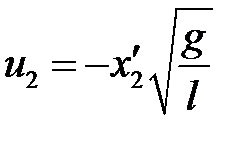После подстановки в закон сохранения импульса получим

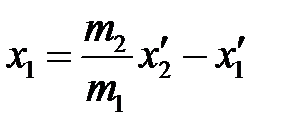. (5.23)

Задание 2.Проверка соотношения (5.23).

Эксперимент проводят точно так же, как и в предыдущем случае.

Задание 3.Реальные тела являются промежуточными между телами абсолютно упругими и абсолютно неупругими, поэтому при соударении реальных тел всегда имеют место и упругие, и остаточные деформации. Коэффициент 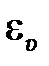восстановления скорости определяется как отношение относительной скорости шаров после удара к относительной скорости шаров до удара:

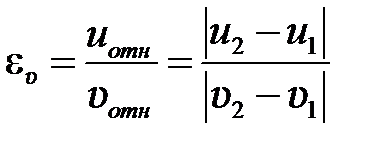. (5.24)

В случае первоначального отклонения большего шара формула (5.24) с учетом (5.20) и (5.21) преобразуется к виду

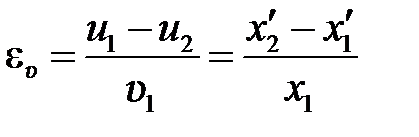. (5.25)

Для абсолютно упругого удара =1. При столкновении реальных шаров <1. При ударе стальных шаров = 0,56, для шаров из слоновой кости = 0,89, для свинцовых шаров близко к нулю.

В случае первоначального отклонения меньшего шара формула (5.25) с учетом (5.21) и (5.22) преобразуется к виду

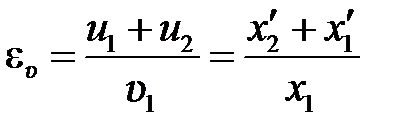. (5.26)

Кроме коэффициента восстановления скорости соударение тел характеризуется коэффициентом 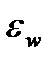восстановления энергии, равным отношению кинетической энергии тел после удара к их кинетической энергии до удара:

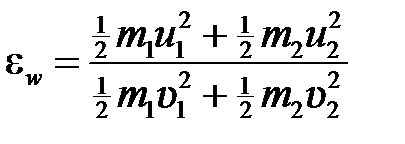. (5.27)

Учитывая, что скорость второго шара до удара 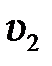= 0 и подставляя для скоростей выражения (5.20) и (5.21), находим рабочую формулу для коэффициента восстановления энергии:

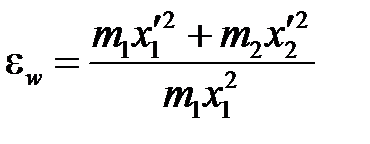. (5.28)

Обработка результатов эксперимента

1. Найдите средние значения величины отскока шаров после удара 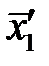и 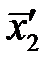по формулам (5.22) и (5.23), соответственно.

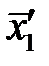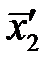2. Используя средние значения и по формулам (5.25),(5.26) и (5.28) определите коэффициенты восстановления скорости 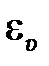и энергии .

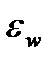3. По методике расчета случайных погрешностей прямых измерений найдите погрешности измерения отклонени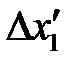й и .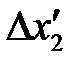

4. Найдите погрешность определения 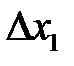по методике вычисления погрешностей косвенных измерений:

а) для случая отклонения большего шара

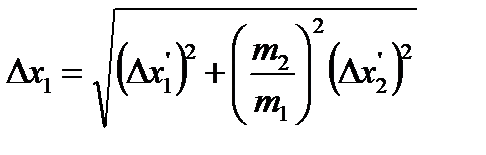; (5.29)

б) для случая отклонения меньшего шара

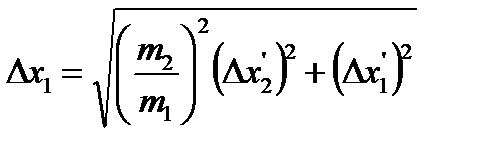. (5.30)

5. Сравните полученное из эксперимента значение x₁ с учетом его приборной погрешности, то есть 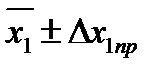со значением x₁, рассчитанным по формуле (5.22) или (5.23). Приборную погрешность 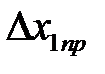определите по цене деления линейки.

6. Погрешность определения коэффициента восстановления 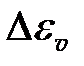скорости определяется по формуле

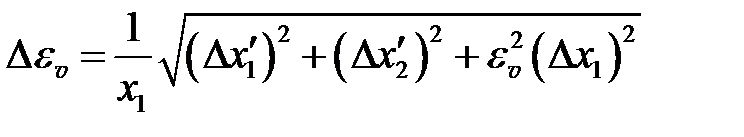. (5.31)

7. Погрешность определения коэффициента восстановления 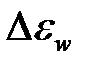энергии определяется по формуле

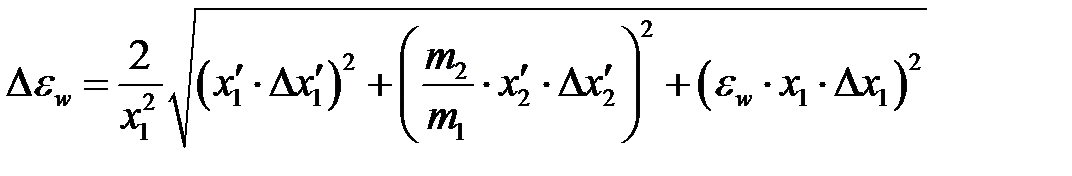. (5.32)

<5 6 789 10 11 >

Дата добавления: 2015-09-25; просмотров: 875;