Капиллярные явления.
| Рис. 6.4. Силы в капилляре |
| h |
| R=r |
| Вода |
| Ртуть |
| h |
| Стекло |
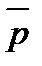
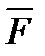
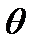 В узких стеклянных трубках, капиллярах, опущенных в жидкость, хорошо заметно поднятие или опускание жидкости. Поверхностная пленка жидкости в трубке под действием молекулярных сил жидкости и стекла принимает вогнутую форму (вогнутый мениск). На такой искривленной поверхности силы поверхностного натяжения вызывают добавочное давление ∆p, обусловленное кривизной поверхности, направленное всегда в сторону вогнутой поверхности.
В узких стеклянных трубках, капиллярах, опущенных в жидкость, хорошо заметно поднятие или опускание жидкости. Поверхностная пленка жидкости в трубке под действием молекулярных сил жидкости и стекла принимает вогнутую форму (вогнутый мениск). На такой искривленной поверхности силы поверхностного натяжения вызывают добавочное давление ∆p, обусловленное кривизной поверхности, направленное всегда в сторону вогнутой поверхности.
Название связано с тем, что высота подъема жидкости велика в достаточно узких трубках, называемых капиллярами.
У верхнего края, где жидкость касается стекла, форма её поверхности очень похожа на полусферу мыльного пузыря, которую мы рассматривали(рис. 6.4). Сила поверхностного натяжения направлена вдоль поверхности жидкости. Вертикальная составляющая этой силы равна
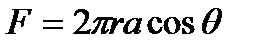 .
.
Она уравновешивается силой тяжести столба жидкости с плотностью 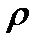 :
: 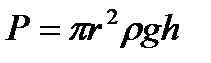 . Таким образом, имеем
. Таким образом, имеем  . Следовательно
. Следовательно
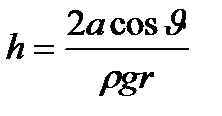 . (6.2)
. (6.2)
Если жидкость в капилляре не смачивающая, уровень её в капилляре оказывается ниже уровня в жидкости в широком сосуде. Это в точности такой же эффект, и описывается он той же формулой (6.2).
Описание экспериментальной установки и последовательность
проведения измерений
| С |
| N |
| M |
| li |
| B |
| L |
| Рис.6.5. Общий вид установки |
1. Определить коэффициент упругости пружины k, для чего на чашечку 2 положить груз m и отметить растяжение пружины x. Вычислить k по формуле
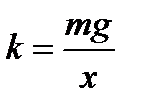 (6.3)
(6.3)
Измерения провести 3−4 раза с разными грузами и затем определить среднее значение  .
.
2. Измерить длину пружины 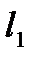 , затем кольцо опустить в сосуд с водой. Сосуд опускать вниз до отрыва кольца от воды. Измерить длину пружины
, затем кольцо опустить в сосуд с водой. Сосуд опускать вниз до отрыва кольца от воды. Измерить длину пружины 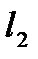 в момент отрыва кольца от воды. Эксперимент провести 5−6 раз.
в момент отрыва кольца от воды. Эксперимент провести 5−6 раз.
3. Измерить штангенциркулем наружный и внутренний диаметры кольца D и d, а затем определить сумму наружной и внутренней длин окружностей кольца L
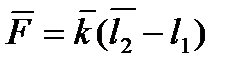 , (6.4)
, (6.4)
а затем найти коэффициент поверхностного натяжения 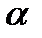
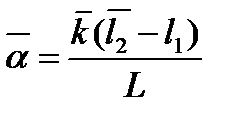 . (6.5)
. (6.5)
Обработка результатов эксперимента
1. Величина полной погрешности определения 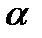 определяется по формуле
определяется по формуле
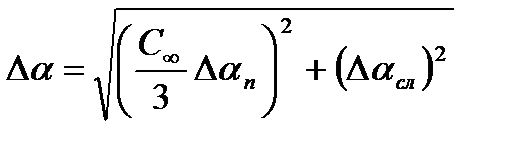 , (6.6)
, (6.6)
где
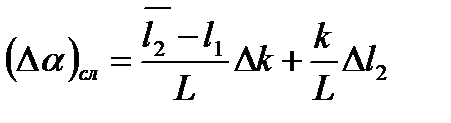 , (6.7)
, (6.7)
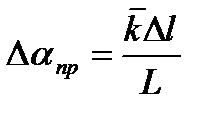 , (6.8)
, (6.8)
где 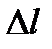 − приборная погрешность линейки.
− приборная погрешность линейки.
Погрешности 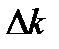 и
и 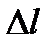 определяются по методике расчета погрешностей прямых измерений.
определяются по методике расчета погрешностей прямых измерений.
2. Результат представить в виде  .
.
Определение коэффициента поверхностного натяжения методом поднятия жидкости в капилляре
Капилляр вставляется в широкий сосуд с исследуемой жидкостью. С помощью масштабной линейки определяется высота подъёма жидкости h. Этот опыт проводится не менее 5 раз.
Если известен радиус r капилляра, то сила поверхностного натяжения:
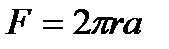 (6.9)
(6.9)
Сила тяжести столба жидкости равна 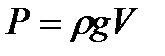 , а так как F=P, то получаем
, а так как F=P, то получаем 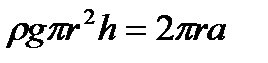 , то есть
, то есть
 . (6.10)
. (6.10)
Обработка результатов и расчёт погрешностей
1. Погрешность величины h определить по методике расчёта погрешностей прямых многократных измерений, задавая доверительную вероятность 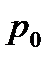 и коэффициент Стьюдента.
и коэффициент Стьюдента.
2. Погрешность косвенных измерений величины a рассчитать по формуле
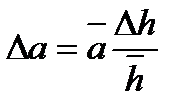 . (6.11)
. (6.11)
3. Результат записать в виде:  .
.
Представляет интерес сравнение величин коэффициентов поверхностного натяжения одной и той же жидкости, полученных различными методами, и погрешностей их определения.
ИЗМЕРЕНИЕ ГАЗОВОЙ ПОСТОЯННОЙ
В молекулярно-кинетической теории объектом исследования является идеализированная модель реального газа − идеальный газ. Идеальным газом называется газ, между молекулами которого отсутствуют силы взаимодействия. При этом принимается, что при соударениях между собой и со стенками сосуда молекулы такого газа ведут себя как абсолютно упругие шарики конечных, но весьма малых размеров. Эти соударения молекул происходят по законам абсолютно упругого удара.
Величинами, определяющими состояние газа, являются: давление р, под которым он находится, его температура Т , объем V, занимаемый определенной массой газа М. Величины p, V, T, M называются параметрами состояния. Давлением Р называется физическая величина, равная пределу отношения численного значения нормальной силы 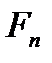 ,действующей на единицу поверхности
,действующей на единицу поверхности 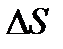 , к величине этой поверхности:
, к величине этой поверхности:
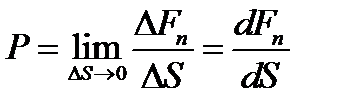
Единицей давления в системе СИ является паскаль ([P]=[F]/[S]= H/ 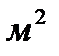 =Па)
=Па)
Температурой называется физическая величина, характеризующая степень нагретости тела.
Параметры состояния связаны между собой различными газовыми законами.
Если газ находится при постоянной температуре T=const, то объем газа и давление связаны законом Бойля-Мариотта pV=const.
При постоянном объеме 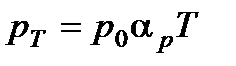 − это закон Шарля, в котором
− это закон Шарля, в котором 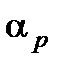 − термический коэффициент давления,
− термический коэффициент давления,  и
и  − давление газа при начальной и конечной температуре.
− давление газа при начальной и конечной температуре.
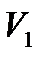 , , 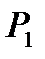 , , 
|
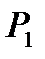 , ,  , , 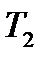
|
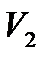 , , 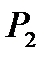 , , 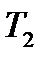
|
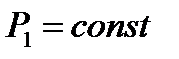
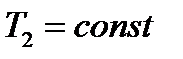
| Рис. 7.1. К выводу уравнения состояния идеального газа |
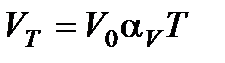 , где
, где 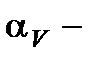 термический коэффициент объемного расширения,
термический коэффициент объемного расширения, 
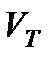 − объемы газа при начальной и конечной температуре.
− объемы газа при начальной и конечной температуре.
Теперь возвращаемся к уравнению состояния идеального газа, то есть найдём связь между P, V и T. Рассмотрим определённую массу газа m, которая заполняет объём 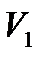 , имеет давление
, имеет давление 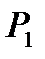 и находится при температуре
и находится при температуре  . Пусть в другом состоянии та же масса газа характеризуется объёмом, давлением и температурой:
. Пусть в другом состоянии та же масса газа характеризуется объёмом, давлением и температурой: 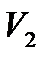 ,
, 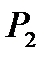 ,
, 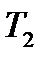 . Установим на основании законов Бойля-Мариотта, Гей-Люссака и Шарля связь между
. Установим на основании законов Бойля-Мариотта, Гей-Люссака и Шарля связь между 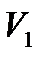 ,
, 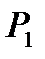 ,
,  и
и 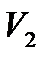 ,
, 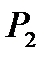 ,
, 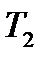 . Для этого сначала газ из состояния
. Для этого сначала газ из состояния 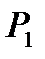 ,
, 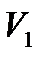 и
и  при постоянном давлении
при постоянном давлении 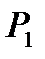 нагреем до температуры
нагреем до температуры 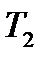 . По закону Гей-Люссака
. По закону Гей-Люссака 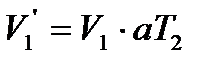 . Так как
. Так как 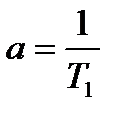 , то
, то 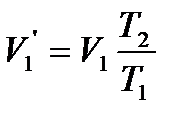 . Из этого состояния в окончательное состояние, характеризующееся параметрами
. Из этого состояния в окончательное состояние, характеризующееся параметрами 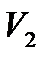 ,
, 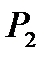 ,
, 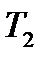 , его можно перевести изотермическим изменением объёма, для которого по закону Бойля-Мариотта имеем:
, его можно перевести изотермическим изменением объёма, для которого по закону Бойля-Мариотта имеем: 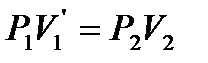 . Подставляя
. Подставляя  , получим
, получим 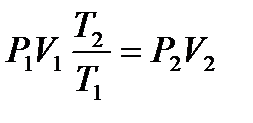 , то есть
, то есть 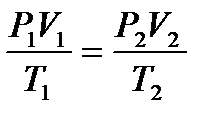 , откуда следует, что при изменении состояния данной массы газа величина PV/T остаётся постоянной, то есть PV/T=B.
, откуда следует, что при изменении состояния данной массы газа величина PV/T остаётся постоянной, то есть PV/T=B.
Если это соотношение относить к одному молю, то постоянная В будет иметь одно и то же значение для всех газов. Эта общая для всех газов постоянная обозначается R и носит название универсальной газовой постоянной. Вводя в предыдущую формулу вместо объема V молярный объем Vо, то есть объем одного моля газа, получим
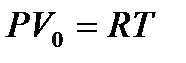 . (7.1)
. (7.1)
Эта формула представляет собой уравнение состояния идеального газа и носит название уравнения Менделеева-Клапейрона.
Уравнение Менделеева-Клапейрона, справедливое для одного моля газа, можно обобщить и на любую массу. Если 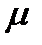 — молярная масса и при некотором данном давлении и температуре 1 моль газа занимает объем
— молярная масса и при некотором данном давлении и температуре 1 моль газа занимает объем 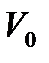 ,то при том же давлении и температуре т граммов газа займут объем
,то при том же давлении и температуре т граммов газа займут объем 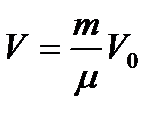 . Тогда
. Тогда 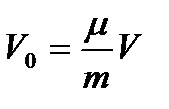 и, подставляя в уравнение Менделеева-Клапейрона (7.1), получим
и, подставляя в уравнение Менделеева-Клапейрона (7.1), получим
 . (7.2)
. (7.2)
В работе предлагается на опыте убедиться в справедливости формулы (7.2), а также определить универсальную газовую постоянную.
Описание лабораторной установки и последовательность проведения измерений
| Рис. 7.2.Экспериментальная установка |
Задание 1. Проверка уравнения состояния идеального газа (7.2).
При равенстве уровней воды в трубках 3 и 5 измеряется длина воздушного столба  от уровня воды в трубке 1. Объём воздуха пропорционален длине столба
от уровня воды в трубке 1. Объём воздуха пропорционален длине столба  плюс объём колбы
плюс объём колбы 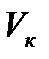 , то есть
, то есть  . Давление воздуха равно атмосферному
. Давление воздуха равно атмосферному 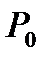 . Температура воздуха
. Температура воздуха 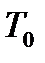 равна температуре воздуха в лаборатории и определяется по термометру. Параметры указанного состояния
равна температуре воздуха в лаборатории и определяется по термометру. Параметры указанного состояния  ,
, 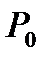 ,
, 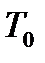 , а величина
, а величина 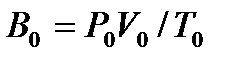 .
.
Включается нагреватель, и температура воды в стакане увеличивается до 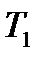 . При этом уровень воды в трубке 5 поднимается, то есть газ в колбе 1 расширяется и его часть
. При этом уровень воды в трубке 5 поднимается, то есть газ в колбе 1 расширяется и его часть 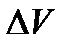 выходит из объёма колбы. Если перемещать трубку 5 вверх − вниз на величину
выходит из объёма колбы. Если перемещать трубку 5 вверх − вниз на величину 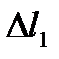 , то можно добиться равенства уровня воды в трубках 3 и 5. Тогда давление воздуха в колбе 1 будет равно атмосферному давлению
, то можно добиться равенства уровня воды в трубках 3 и 5. Тогда давление воздуха в колбе 1 будет равно атмосферному давлению  , а длина воздушного столба или объём
, а длина воздушного столба или объём  , где
, где 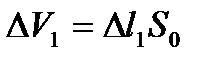 ,
, 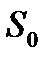 − поперечное сечение трубки. Получаются вторые данные
− поперечное сечение трубки. Получаются вторые данные  ,
, 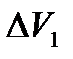 ,
, 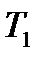 . Далее вода в стакане нагревается до температуры
. Далее вода в стакане нагревается до температуры  и проделывается то же, что и с холодной водой. Получается третий набор данных:
и проделывается то же, что и с холодной водой. Получается третий набор данных:  ,
, 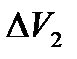 ,
, 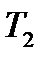 . Все полученные данные измерений заносятся в таблицу.
. Все полученные данные измерений заносятся в таблицу.
Величина 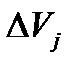 (j=1,2) рассчитывается следующим образом. В каждом эксперименте при нагревании колбы до температуры
(j=1,2) рассчитывается следующим образом. В каждом эксперименте при нагревании колбы до температуры 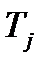 объём газа в ней увеличивается на
объём газа в ней увеличивается на 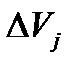 , и при этом высота жидкости в манометре изменяется на
, и при этом высота жидкости в манометре изменяется на 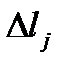 . Поэтому на основании уравнения (7.2)
. Поэтому на основании уравнения (7.2)
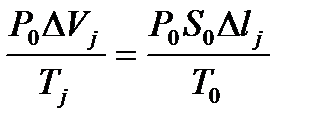 ,
,
откуда изменение объёма равно 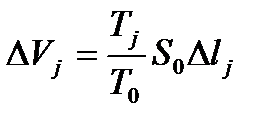 , то есть
, то есть 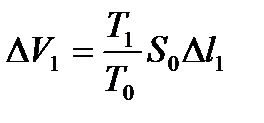 , а
, а 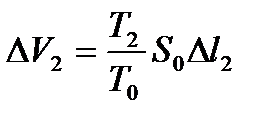 .
.
Обработка результатов и расчёт погрешностей
1. Приборную погрешность величины 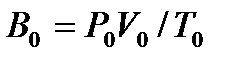 определить по формуле
определить по формуле
 . (7.3)
. (7.3)
2. Результат представить в виде 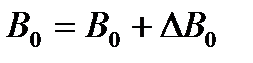 .
.
3. Погрешность величины 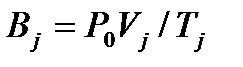 (j=1,2) рассчитать по формуле
(j=1,2) рассчитать по формуле
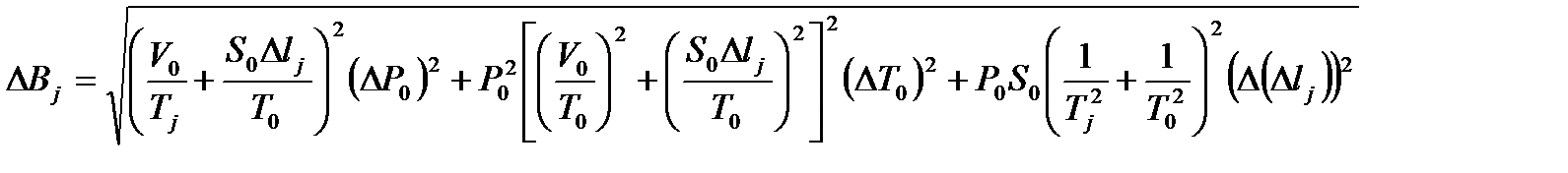 . (7.4)
. (7.4)
4. Результат представить в виде: 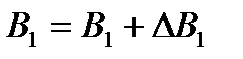 ,
, 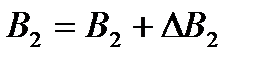 .
.
5. Сравнить величины 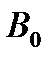 ,
, 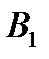 ,
, 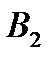 и сделать вывод о формуле (7.2).
и сделать вывод о формуле (7.2).
Задание 2. Определение универсальной газовой постоянной
Обработка результатов и расчёт погрешностей.
1. Величину газовой постоянной для двух случаев j 1,2 рассчитать по формуле
 , (7.5)
, (7.5)
считая, что величины 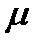 и
и 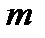 являются приборными константами.
являются приборными константами.
2. Погрешность  вычислить с учётом зависимости (7.4) по формуле
вычислить с учётом зависимости (7.4) по формуле
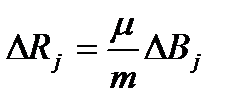 . (7.6)
. (7.6)
3. Результат представить в виде 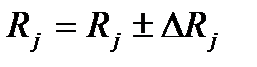 , j=1,2.
, j=1,2.
4. Сравнить величины 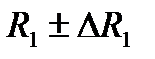 и
и 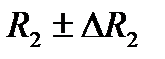 с табличным значением R.
с табличным значением R.
Задание 3. Определение газовой постоянной методом измерения объема и давления паров жидкости.
Если в сосуд известного объема ввести определенную массу легко испаряющейся жидкости, а после того, как она полностью испарится, измерить, насколько увеличится давление внутри сосуда, то, зная молекулярную массу жидкости и температуру, можно вычислить R по формуле
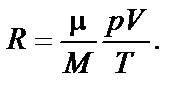 (7.7)
(7.7)

| Рис. 7.3 Схема экспериментальной установки |
В сосуд вводится ацетон из микробюретки: 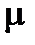 ац= 0,058 кг/моль,
ац= 0,058 кг/моль, 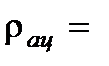 790 кг/м3,
790 кг/м3,
 , (7.8)
, (7.8)
где Vац – объем ацетона, введенного в сосуд.
Так как парциальное давление паров ацетона измеряется водяным манометром по разности уровней воды в его коленах, то
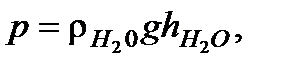 (7.9)
(7.9)
где 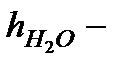 разность уровней воды в коленах манометра.
разность уровней воды в коленах манометра.
Учитывая (7.8) и (7.9), можно записать
 (7.10)
(7.10)
Первый сомножитель в (7.8) является величиной постоянной, второй − постоянен для конкретных условий проведения опыта при постоянной температуре и объеме сосуда. Таким образом определение R сводится к измерению объема жидкого ацетона, введенного в сосуд, и разности уровней воды в коленах манометра, обусловленной давлением паров ацетона. Точный объем сосуда с учетом объема резинового шланга, соединяющего сосуд с манометром и объема трубки манометра до уровня нулевой отметки написан на стенке сосуда. Работа выполняется в такой последовательности:
1. Измеряется объем ацетона микробюретке.
2. Открывается кран у тройника 9 и перемещением правого колена манометра уровень воды устанавливается на нулевую отметку шкалы. После этого закрывается кран 9.
3. Весь ацетон из микробюретки выливается в сосуд, в результате чего изменяются показания манометра. После того, как весь ацетон испарится, показания манометра перестанут изменяться.
4. Передвижением правого колена манометра устанавливается уровень воды в левом колене на нулевую отметку. Это необходимо сделать для сохранения объема воздуха в сосуде и трубках таким же, как в начале опыта. Тогда манометр покажет только парциальное давление паров ацетона, так как температура не изменилась.
5. По шкале манометра отсчитывается разность уровней воды и в его коленах и данные записываются в таблицу.
Обработка результатов
1. Газовая постоянная вычисляется по формуле (7.11).
2. Так как измеряется только одна переменная 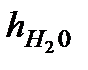 один раз, то предельная погрешность косвенных измерений величины R определяется по формуле
один раз, то предельная погрешность косвенных измерений величины R определяется по формуле
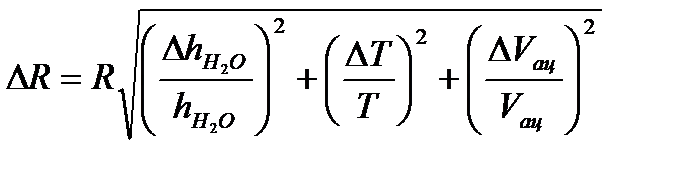 , (7.11)
, (7.11)
где  ,
, 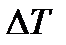 и
и 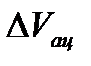 − систематические погрешности определения разности уровней в манометре после испарения ацетона, температуры и объёма ацетона.
− систематические погрешности определения разности уровней в манометре после испарения ацетона, температуры и объёма ацетона.
3. Сравниваются величины газовой постоянной, полученные разными методами, и погрешности этих методов.
4. Если измерения проводятся несколько раз, то процедура расчёта погрешностей несколько отличается. В этом случае при измерениях изменяются две величины: 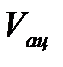 ,
, 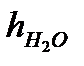 . Поэтому
. Поэтому
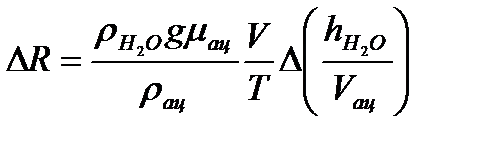 , (7.12)
, (7.12)
где погрешность величины 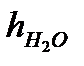 /
/ 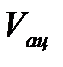 необходимо определить по методике расчёта погрешностей прямых многократных измерений, задавая доверительную вероятность
необходимо определить по методике расчёта погрешностей прямых многократных измерений, задавая доверительную вероятность 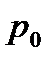 и коэффициент Стьюдента.
и коэффициент Стьюдента.
ТЕПЛОЕМКОСТЬ ЖИДКОСТИ
Рис. 8.1. Двух (а) и трехатомная (б) молекула
 Количество независимых координат, характеризующих положение материального объекта в пространстве, называется числом его степеней свободы. Молекулу одноатомного идеального газа можно рассматривать как материальную точку, так как ее масса сосредоточена в ядре малого размера. Такая молекула (атом) имеет три степени свободы, то есть для описания ее поступательного движения требуется три независимых координаты. Для того чтобы охарактеризовать положение в пространстве двухатомной молекулы, состоящей из жестко связанных атомов, необходимо задать пять независимых координат. Из них три служат для описания ее поступательного движения, а две характеризуют вращательное движение вокруг осей
Количество независимых координат, характеризующих положение материального объекта в пространстве, называется числом его степеней свободы. Молекулу одноатомного идеального газа можно рассматривать как материальную точку, так как ее масса сосредоточена в ядре малого размера. Такая молекула (атом) имеет три степени свободы, то есть для описания ее поступательного движения требуется три независимых координаты. Для того чтобы охарактеризовать положение в пространстве двухатомной молекулы, состоящей из жестко связанных атомов, необходимо задать пять независимых координат. Из них три служат для описания ее поступательного движения, а две характеризуют вращательное движение вокруг осей 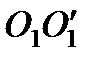 и
и 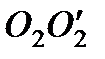 (рис. 8.1). Трехатомная молекула имеет три вращательные степени свобода. Реальные молекулы не являются системами жестко связанных атомов. Так как атомы могут колебаться друг относительно друга, появляются дополнительные колебательные степени свободы.
(рис. 8.1). Трехатомная молекула имеет три вращательные степени свобода. Реальные молекулы не являются системами жестко связанных атомов. Так как атомы могут колебаться друг относительно друга, появляются дополнительные колебательные степени свободы.
Одним из основных положений классической молекулярно-кинетической теории является закон равномерного распределения энергии по степеням свободы: на каждую поступательную, а также вращательную степень свободы газовой молекулы приходится одинаковая энергия, равная  . При колебательном движении молекулы имеют и кинетическую
. При колебательном движении молекулы имеют и кинетическую 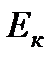 и потенциальную
и потенциальную 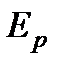 энергию. При этом если колебания гармонические, то
энергию. При этом если колебания гармонические, то  и на основании закона равнораспределения энергии по степеням свободы полная энергия, приходящаяся на одну колебательную степень свободы, равна
и на основании закона равнораспределения энергии по степеням свободы полная энергия, приходящаяся на одну колебательную степень свободы, равна 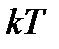 . Она вдвое превышает среднюю энергию на одну степень свободы поступательного или вращательного движения.
. Она вдвое превышает среднюю энергию на одну степень свободы поступательного или вращательного движения.
Если считать, что в газах, жидкостях и твердых телах молекулы колеблются независимо друг от друга, то на три колебательные степени свободы каждой молекулы приходится энергия
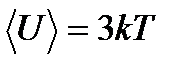 . (8.1)
. (8.1)
Полная внутренняя энергия одного моля такой системы молекул равна:
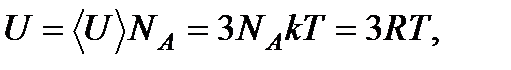 (8.2)
(8.2)
где 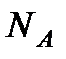 − число Авогадро,
− число Авогадро,  − универсальная газовая постоянная.
− универсальная газовая постоянная.
Молярной теплоемкостью называется количество энергии, поглощаемой одним молем вещества при нагревании на 1 К, то есть
 (8.3)
(8.3)
Это закон Дюлонга и Пти: молярные теплоемкости химически простых веществ одинаковы и не зависят от температуры.
Закон Дюлонга и Пти хорошо выполняется при комнатной температур. Для более низкой температуры наблюдаются отклонения, связанные с тем, что энергию колебательного движения молекул нельзя вычислять на основании закона о равнораспределении энергии по степеням свободы. Теплоемкость в этой области уменьшается, стремясь к нулю при 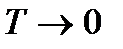 .
.
Качественное согласие с результатами эксперимента было достигнуто в теории Эйнштейна, в которой предполагалось, что молекула представляет собой не классический, а квантово-механический гармонический осциллятор, средняя энергия которого определяется соотношением:
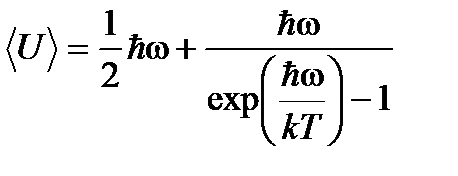 , (8.4)
, (8.4)
где 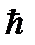 − приведенная постоянная Планка,
− приведенная постоянная Планка,  − частота гармонического осциллятора. Используя для внутренней энергии кристалла формулу (8.2) и дифференцируя по температуре, находим молярную теплоемкость:
− частота гармонического осциллятора. Используя для внутренней энергии кристалла формулу (8.2) и дифференцируя по температуре, находим молярную теплоемкость:
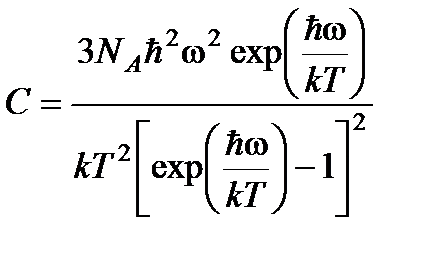 . (8.5)
. (8.5)
При высоких температурах 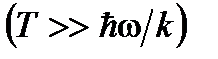 из (8.5) имеем
из (8.5) имеем 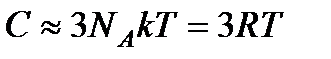 , что совпадает с законом Дюлонга и Пти (8.2). При низких температурах
, что совпадает с законом Дюлонга и Пти (8.2). При низких температурах 

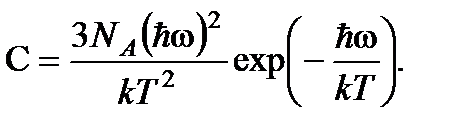 (8.6)
(8.6)
Выражение (8.6) при 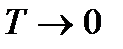 приближается к нулю по экспоненциальному закону (рис. 8.2, левая часть графика).
приближается к нулю по экспоненциальному закону (рис. 8.2, левая часть графика).
| Рис. 8.2. Зависимость теплоемкости от температуры |
 довольно сложная и ее трудно реализовать для структур со сложными молекулами, например, для органических жидкостей. Поэтому на практике применяются экспериментальные методы определения теплоемкости, в частности, калориметрический метод.
довольно сложная и ее трудно реализовать для структур со сложными молекулами, например, для органических жидкостей. Поэтому на практике применяются экспериментальные методы определения теплоемкости, в частности, калориметрический метод.
Описание экспериментальной установки
Калориметр представляет собой сосуд 1, стенки которого теплоизолированы между собой с помощью прокладки из теплоизолирующего материала 2, а также от окружающей среды крышкой 3. В сосуд помещается исследуемое вещество 4 (в нашем случае жидкость), температура которой определяется термометром 5. Нагревание жидкости осуществляется нагревателем 6, мощность которого определяется по току, регистрируемому стрелочным прибором (рис. 8.3). Для изменения тока применяется реостат R. Для улучшения условий теплообмена жидкость в эксперименте перемешивается специальной мешалкой 7, которая вращается электродвигателем.
 Теплота нагревателя
Теплота нагревателя 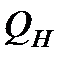 расходуется на нагревание жидкости
расходуется на нагревание жидкости 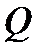 , калориметра со всеми его деталями, термометром, мешалкой и прочим
, калориметра со всеми его деталями, термометром, мешалкой и прочим 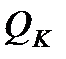 , также тепловые потери
, также тепловые потери 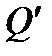 на излучение, неидеальность теплоизоляции и другое.
на излучение, неидеальность теплоизоляции и другое.
| Рис. 8.3. Экспериментальная установка |
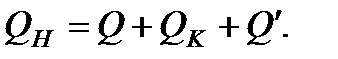 (8.7)
(8.7)
Теплоемкость исследуемой жидкости в интервале температур от  до
до 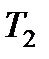 определим как количество тепла
определим как количество тепла 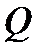 , необходимое для нагревания единицы ее массы на 1 градус Кельвина, то есть
, необходимое для нагревания единицы ее массы на 1 градус Кельвина, то есть
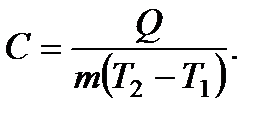 (8.8)
(8.8)
Поэтому
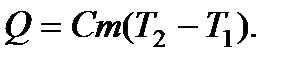 (8.9)
(8.9)
С учетом этого уравнение теплового баланса записывается в виде
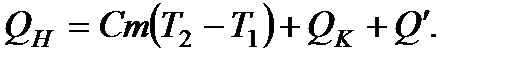 (8.10)
(8.10)
Если бы тепловые потери отсутствовали, 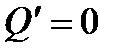 , то нагревание жидкости произошло бы до более высокой температуры
, то нагревание жидкости произошло бы до более высокой температуры 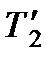 , и тогда уравнение теплового баланса (8.10) перепишется в виде
, и тогда уравнение теплового баланса (8.10) перепишется в виде
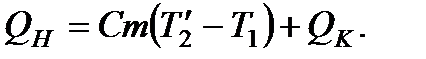 (8.11)
(8.11)
Пусть 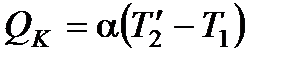 , где
, где  - постоянная калориметра, которую в дальнейшем надо определить.
- постоянная калориметра, которую в дальнейшем надо определить.
Тогда из формулы (8.11) получим
 (8.12)
(8.12)
Отсюда теплоемкость жидкости в калориметре
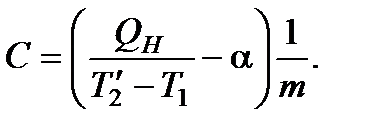 (8.13)
(8.13)
 Таким образом, для определения теплоемкости исследуемой жидкости необходимо знать температуру
Таким образом, для определения теплоемкости исследуемой жидкости необходимо знать температуру  и постоянную калориметра
и постоянную калориметра 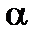 . Найти их можно следующим образом.
. Найти их можно следующим образом.
| Рис. 8.4. Диаграмма нагревания жидкости в калориметре |
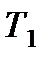 (линия а-b, рис. 8.4). При включении в момент
(линия а-b, рис. 8.4). При включении в момент 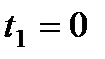 нагревателя температура возрастает до значения
нагревателя температура возрастает до значения 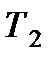 по кривой b-d. После выключения нагревателя происходит процесс охлаждения, характеризуемый дифференциальным уравнением:
по кривой b-d. После выключения нагревателя происходит процесс охлаждения, характеризуемый дифференциальным уравнением:
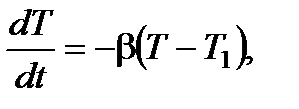 (8.14)
(8.14)
где 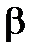 − постоянная охлаждения.
− постоянная охлаждения.
Согласно (8.14) скорость убывания температуры пропорциональна разности температур установки и окружающей среды.
Из (8.14) находим
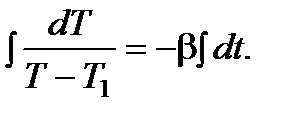 (8.15)
(8.15)
Выполняя интегрирование, получим
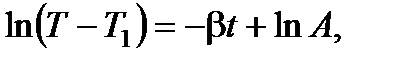 (8.16)
(8.16)
где А − константа интегрирования, которая должна быть определена из начального условия 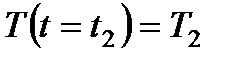 :
:
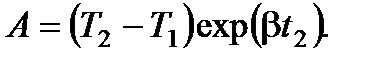 (8.17)
(8.17)
Из (8.16) и (8.17) находим
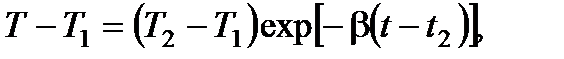 (8.18)
(8.18)
что соответствует экспоненциальному участку кривой d-e.
Если бы потери отсутствовали, то процесс нагревания происходил бы по кривой a-b-c до температуры 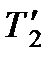 , а охлаждение – по кривой c-d-e в соответствии с экспоненциальной зависимостью (8.18). Таким образом величину температуры
, а охлаждение – по кривой c-d-e в соответствии с экспоненциальной зависимостью (8.18). Таким образом величину температуры 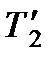 можно найти из (8.18) при
можно найти из (8.18) при 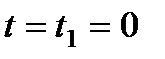 по формуле
по формуле
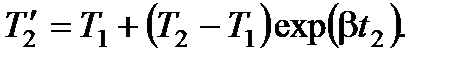 (8.19)
(8.19)
Величина постоянной  находится по экспериментальному значению температуры на участке охлаждения d-e, например, в момент времени
находится по экспериментальному значению температуры на участке охлаждения d-e, например, в момент времени 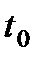 :
:
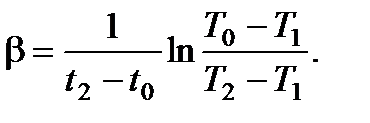 (8.20)
(8.20)
Чтобы найти постоянную калориметра, необходимо провести дополнительный эксперимент с жидкостью, теплоемкость которой хорошо известна, например с водой. Тогда из уравнения теплового баланса (8.12) можно найти постоянную калориметра 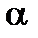 :
:
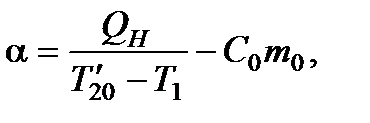 (8.21)
(8.21)
где 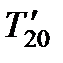 − температура точки с (рис. 8.4) при нагревании воды,
− температура точки с (рис. 8.4) при нагревании воды, 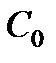 − средняя теплоемкость воды в интервале
− средняя теплоемкость воды в интервале 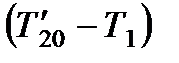 ,
, 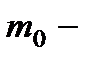 масса воды в калориметре.
масса воды в калориметре.
Методика эксперимента
1. В калориметр заливается вода при комнатной температуре 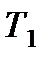
2. Одновременно включается нагреватель, мешалка и секундомер, регистрируется ток через нагреватель, через некоторое время (порядка минуты) фиксируется значение температуры. Данные заносятся в таблицу.
3. Когда вода нагреется на 10 градусов, нагреватель выключается. Вследствие инерции нагревателя после выключения тока температура некоторое время возрастает, затем начинает спадать, что также фиксируется, а данные записываются в таблицу.
4. После полного охлаждения воды она выливается из калориметра, который заполняется исследуемой жидкостью и опыт повторяется. Данные заносятся в таблицу.
Обработка результатов
1. По данным полученным в п.1. строится график зависимости температуры от времени нагревания для калориметра с водой.
2. По формуле (8.20) определяется величина  .
.
3. По формуле (8.19) вычисляется температура  .
.
4. По формуле (8.21) рассчитывается постоянная калориметра 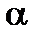 .
.
При этом величина 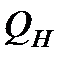 определяется по формуле
определяется по формуле
 (8.22)
(8.22)
где 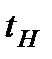 − момент времени отключения нагревателя,
− момент времени отключения нагревателя, 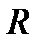 − полное сопротивление цепи нагревателя, указанное на стенде.
− полное сопротивление цепи нагревателя, указанное на стенде.
5. По данным получившимся в п. 2 строится график зависимости температуры от времени нагревания для калориметра с исследуемой жидкостью.
6. По формуле (8.20) находится величина 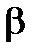 .
.
7. По формуле (8.19) вычисляется температура 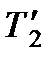 .
.
8. По формуле (8.13) и найденному ранее значению постоянной калориметра вычисляется теплоемкость исследуемой жидкости. При этом 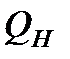 рассчитывается по формуле (8.22).
рассчитывается по формуле (8.22).
9. По методике расчета погрешностей косвенных измерений осуществить расчет погрешности постоянной охлаждения 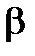 для воды по формуле:
для воды по формуле:
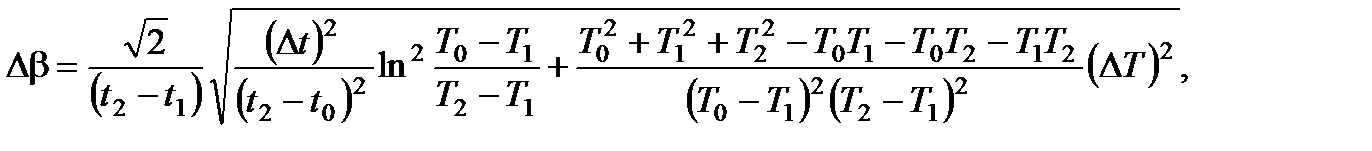 (8.23)
(8.23)
где 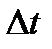 и
и  − систематические погрешности измерения времени и температуры.
− систематические погрешности измерения времени и температуры.
10. Найти погрешность определения температуры 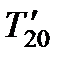 для воды:
для воды:
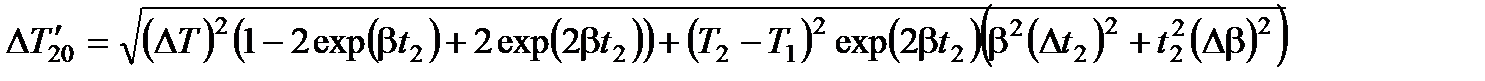 (8.24)
(8.24)
11. Для воды определить погрешность 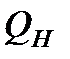 :
:
 , (8.25)
, (8.25)
где 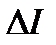 - погрешность тока, определяемая классом точности амперметра.
- погрешность тока, определяемая классом точности амперметра.
12. Определить погрешность постоянной калориметра  :
:
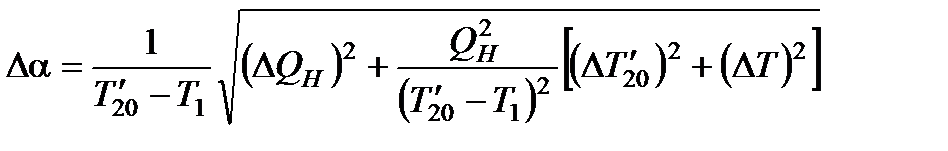 . (8.26)
. (8.26)
13. Найти погрешность определения постоянной охлаждения 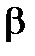 , температуры
, температуры 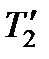 и теплоты нагревателя
и теплоты нагревателя 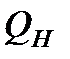 для исследуемой жидкости по формулам (8.23), (8.24) и (8.25).
для исследуемой жидкости по формулам (8.23), (8.24) и (8.25).
14. Вычислить погрешность определения теплоемкости исследуемой жидкости по формуле
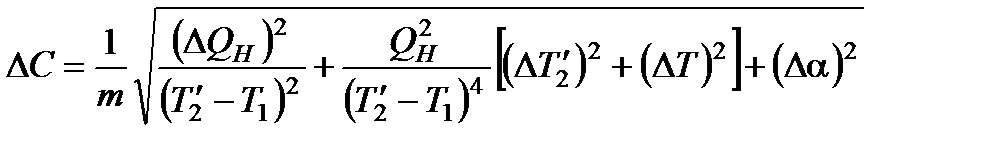 . (8.27)
. (8.27)
15.Представить окончательный результат в виде
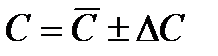 , (8.28)
, (8.28)
где 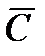 − значение теплоемкости исследуемой жидкости полученное по формуле (8.13).
− значение теплоемкости исследуемой жидкости полученное по формуле (8.13).
КОЛЕБАНИЯ СТРУНЫ
Пусть точка, совершающая колебания, находится в среде, все частицы которой связаны между собой. Тогда энергия колебаний точки может передаваться окружающим точкам, вызывая их колебания. Явление распространения колебаний в среде называется волной. При этом колеблющиеся частицы не перемещаются с распространяющимся колебательным процессом, а колеблются около своих положений равновесия.
Если в неограниченной среде беспрепятственно распространяется единственная волна, то она называется бегущей. Составим уравнение бегущей волны, позволяющее определять смещение любой точки волны в любой момент времени.
| Рис. 9.1. К выводу уравнения бегущей волны |
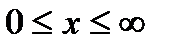 − струну, которая на конце x=0 присоединена к источнику гармонических колебаний в момент времени t’:D(t’)=Asin
− струну, которая на конце x=0 присоединена к источнику гармонических колебаний в момент времени t’:D(t’)=Asin 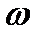 t’. Найдём смещение элементов струны, как функцию координаты x и времени t, то есть функцию
t’. Найдём смещение элементов струны, как функцию координаты x и времени t, то есть функцию  . Очевидно, что для точки x=0,
. Очевидно, что для точки x=0, 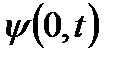 =D(t’)=Asin
=D(t’)=Asin 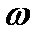 t’ (рис. 9.1). Предположим, что бегущее по струне
t’ (рис. 9.1). Предположим, что бегущее по струне 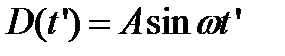
|
| x = 0 |
| z |
| (t') |
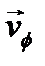
|
| x |
| (t) |
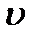 . Смещение элемента струны x в момент t равно смещению элемента x=0 в момент t’
. Смещение элемента струны x в момент t равно смещению элемента x=0 в момент t’  =
= 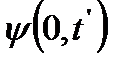 , если расстояние между ними равно расстоянию, которое возмущение проходит за время t-t’ со скоростью
, если расстояние между ними равно расстоянию, которое возмущение проходит за время t-t’ со скоростью 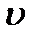 . Тогда точки x=0 и x=x колеблются в одной фазе: x=
. Тогда точки x=0 и x=x колеблются в одной фазе: x= 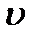 (t-t’),
(t-t’), 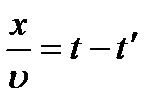 ,
, 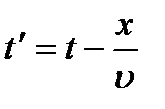 . Поэтому уравнение бегущей синусоидальной волны
. Поэтому уравнение бегущей синусоидальной волны  =
= 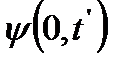 = Asin
= Asin 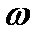 t’, то есть
t’, то есть
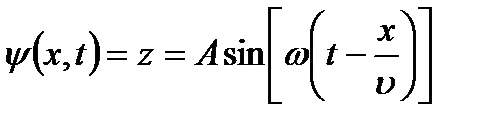 . (9.1)
. (9.1)
Преобразуем функцию (9.1): 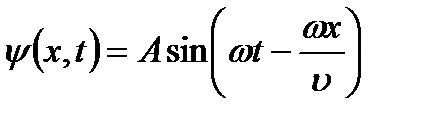 . Обозначим
. Обозначим  =k и назовём его волновым числом, тогда
=k и назовём его волновым числом, тогда  =
= 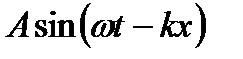 . Следовательно, скорость
. Следовательно, скорость  ,
, 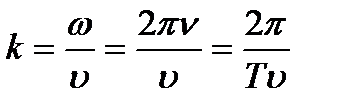 . Величину
. Величину 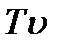 , равную расстоянию, которое возмущение преодолевает за период колебаний, назовём длиной волны, то есть
, равную расстоянию, которое возмущение преодолевает за период колебаний, назовём длиной волны, то есть 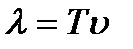 , тогда
, тогда 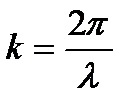 ,
, 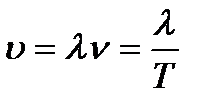 .
.
Уравнение (9.1) и есть уравнение бегущей одномерной (или плоской) волны. При заданном x оно позволяет определить положение точки (с координатой равновесного положения x) в любой момент времени t. При заданном t оно позволяет определить мгновенные положения всех колеблющихся точек.
Таким образом, видим, что в волновом движении имеет место двоякая периодичность. С одной стороны, каждая частица среды совершает периодическое движение во времени, с другой стороны, в каждый момент времени все частицы располагаются на линии, форма которой периодически повторяется в пространстве.
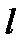
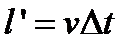
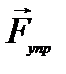

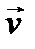
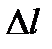 Определим скорость распространения продольных колебаний вдоль бесконечно длинного стержня с постоянным поперечным сечением.
Определим скорость распространения продольных колебаний вдоль бесконечно длинного стержня с постоянным поперечным сечением.
| Рис. 9.2. Распространение упругой деформации вдоль стержня |
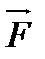 (рис. 9.2) вблизи этого сечения происходит уплотнение материала стержня, и возникает деформация сжатия. Появляются упругие силы, стремящиеся восстановить первоначальную плотность, в результате чего возникает сжатие соседних областей и таким образом локальное возмущение плотности вблизи левого края стержня распространяется вправо со скоростью
(рис. 9.2) вблизи этого сечения происходит уплотнение материала стержня, и возникает деформация сжатия. Появляются упругие силы, стремящиеся восстановить первоначальную плотность, в результате чего возникает сжатие соседних областей и таким образом локальное возмущение плотности вблизи левого края стержня распространяется вправо со скоростью 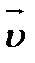 . Импульс силы упругости
. Импульс силы упругости 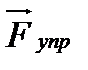 равен
равен 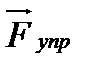
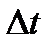 . Если Е − модуль сжатия, иначе называемый модулем Юнга, то
. Если Е − модуль сжатия, иначе называемый модулем Юнга, то 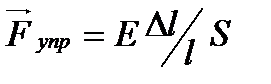 . За время
. За время 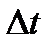 деформация распространяется на расстояние
деформация распространяется на расстояние 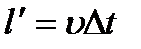 . Масса участка стержня, охваченная деформацией, увеличится на
. Масса участка стержня, охваченная деформацией, увеличится на  вследствие увеличения плотности материала на
вследствие увеличения плотности материала на 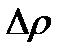 . Так как
. Так как 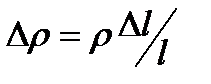 , то
, то 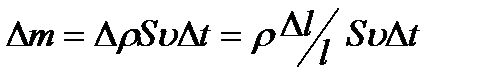 . В соответствии со вторым зaконом Ньютона импульс силы упругости равен изменению импульса, то есть
. В соответствии со вторым зaконом Ньютона импульс силы упругости равен изменению импульса, то есть 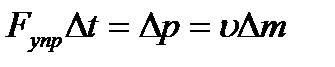 . Подставляя все величины, получим
. Подставляя все величины, получим
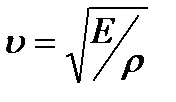 или
или 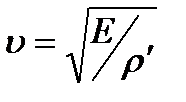 , (9.2)
, (9.2)
где 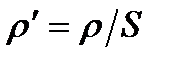 - погодная плотность материала стержня.
- погодная плотность материала стержня.
Уравнение (9.1) описывает волну, распространяющуюся в положительном направлении оси ох. При изменении направления распространения волны на противоположное второе слагаемое в аргументе косинуса изменяет знак, так как  заменяется на
заменяется на 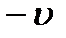
 . (9.3)
. (9.3)
Рассмотрим теперь распространение волны в струне, закрепленной с обеих сторон. При этом волна, движущаяся в одном направлении, достигнув второго закрепленного конца струны, отразится и станет распространяться в противоположном направлении. Таким образом вдоль длины струны возникнет явление наложения волн, распространяющихся в противоположных направлениях. Если свойства среды не изменяются под воздействием распространяющейся волны, то будет выполняться принцип суперпозиции, согласно которому каждая волна распространяется в среде независимо от других. В этом случае результирующее смещение z частиц среды будет определяться как сумма смещений z1 и z2, обусловленных прохождением отдельных волн. В результате будет наблюдаться в различных точках среды усиление или ослабление колебаний в зависимости от фаз приходящих возмущений.
Сложение волн, при котором в разных точках среды образуются усиления и ослабления амплитуды колебаний, называется интерференциейволн. Такая интерференционная картина сохраняется во времени.
Рассмотрим интерференцию двух волн с одинаковой амплитудой, распространяющихся в противоположных направлениях, как в случае струны, закрепленной с обеих сторон. При этом необходимо учитывать следующее явление. После отражения от закрепленного конца отраженная деформация имеет противоположный знак. Это становится понятным, если учесть, что так, как смещение закрепленного конца все время отсутствует, у точки крепления развиваются силы, препятствующие приходящему изгибу струны. Эти силы порождают изгиб противоположного знака, начинающий распространяться в обратную сторону. Поэтому и в отраженной деформации знак смещения изменяется на обратный. Если отражается гармоническая волна, то такое изменение равносильно «потере» полуволны при отражении.
Таким образом, наложение двух волн даст следующее:
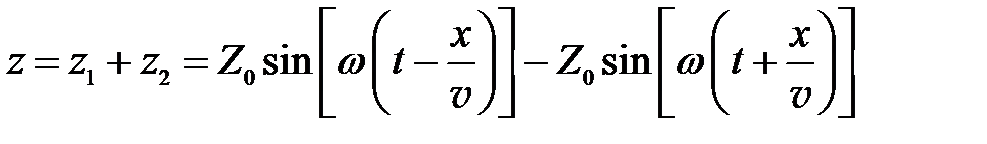 .
.
Используя формулу разности синусов, получим
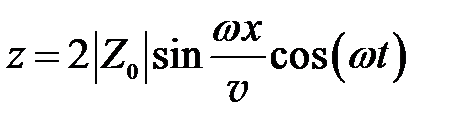 . (9.4)
. (9.4)
Это выражение называется уравнением стоячей волны, при этом предполагается режим установившихся колебаний, то есть режим, возникающий после многократного пробега волн между креплениями струны. Из (9.4) видно, что в стоячей волне все точки среды (любое значение x) колеблются по гармоническому закону с круговой частотой w.
Амплитуда колебаний различна для разных точек и определяется из (9.4) следующим образом:

| Рис. 9.3. Различные моды колебаний струны |
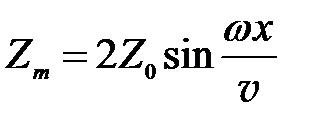 . (9.5)
. (9.5)
Из последнего выражения вытекает, что есть точки среды, называемые узлами, в которых колебания отсутствуют Zm = 0, следовательно, z = 0. Координаты этих точек определятся из условия равенства нулю синуса в выражении (9.5), то есть
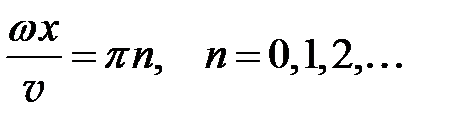 . (9.6)
. (9.6)
Отсюда, так как  , получаем
, получаем
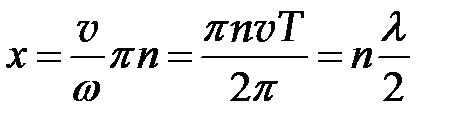 .
.
Следовательно, расстояние между соседними узлами равно половине длины волны. Так как узлы все время остаются в покое, то в стоячей волне нет направленного переноса энергии, энергия не может перейти через узел. Передача энергии по струне производится только бегущей волной.
Те точки, в которых значение амплитуды достигает максимума 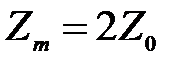 , называются пучностями. Как следует из выражения (9.5), координаты этих точек определяются из условия
, называются пучностями. Как следует из выражения (9.5), координаты этих точек определяются из условия 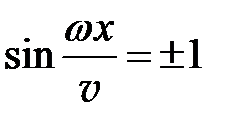 , то есть отвечают уравнению
, то есть отвечают уравнению 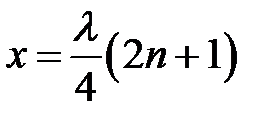 . Видим, что расстояние между соседними пучностями также равно половине длины волны.
. Видим, что расстояние между соседними пучностями также равно половине длины волны.
Множитель  при переходе через узел меняет знак, вследствие чего фаза колебаний по разные стороны от узла отличается на p. Все точки, находящиеся между двумя соседними узлами, колеблются в одинаковой фазе (их отклонения имеют одинаковый знак). Условие неподвижности обоих концов закрепленной струны приводит к тому, что на длине струны должно укладываться целое число полуволн:
при переходе через узел меняет знак, вследствие чего фаза колебаний по разные стороны от узла отличается на p. Все точки, находящиеся между двумя соседними узлами, колеблются в одинаковой фазе (их отклонения имеют одинаковый знак). Условие неподвижности обоих концов закрепленной струны приводит к тому, что на длине струны должно укладываться целое число полуволн:
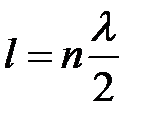 . (9.7)
. (9.7)
Таким образом, стоячая волна образуется только при надлежащем соотношении размеров струны и длины волны (частоты колебаний). Для разных значений n = 1, 2,… получим различные типы, или моды, колебаний, при этом n определяет число пучностей, а не узлов. Из (9.6) с учетом (9.7) получим формулу для частот, при которых в струне устанавливаются стоячие волны
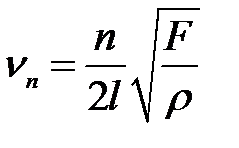 , (9.8)
, (9.8)
Частоты 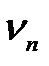 называют собственными частотами струны. Частоту
называют собственными частотами струны. Частоту 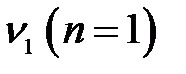 называют основной частотой, остальные
называют основной частотой, остальные  – обертонами. Видим, что определяемые формулой (9.8) собственные частоты не зависят от модуля Юнга материала. Этот результат является следствием того, что мы пренебрегли изменением натяжения струны при колебаниях.
– обертонами. Видим, что определяемые формулой (9.8) собственные частоты не зависят от модуля Юнга материала. Этот результат является следствием того, что мы пренебрегли изменением натяжения струны при колебаниях.
В общем случае в струне могут одновременно существовать колебания с различными собственными частотами. Так, наряду с основным тоном n = 1, могут возбуждаться обертоны n = 2, 3, 4,….
Полученные выше уравнения описывают движение идеально гибкой струны в вакууме. При колебаниях реальной струны всегда происходят потери энергии.
Часть энергии теряется вследствие трения о воздух, другая часть уходит через концы струны и т.д. Для поддержания незатухающих колебаний служит вибратор. Если энергия потерь в точности компенсируется энергией, поступающей от вибратора, то в струне можно наблюдать стоячие волны. Но теперь по струне должна происходить передача энергии. Поэтому наряду со стоячими будут существовать бегущие волны, в результате чего узлы окажутся несколько размытыми. Если потери энергии за период малы по сравнению с запасом колебательной энергии в струне, то искажение стоячих волн бегущей волной будет незначительным.
Другим приближением в изложенной выше теории является пренебрежение неоднородностью струны. В реальной струне и плотность, и натяжение могут являться непрерывными функциями координаты Х. Например, если струна подвешена вертикально, то учет массы струны приведет к тому, что натяжение в верхних частях будет больше, чем внизу. Любая неоднородность приведет к искажению формы колебаний, так как синусоидальные колебания в пространстве характерны только для нормальных мод однородных систем.
Дата добавления: 2015-09-25; просмотров: 1131;
