Экспериментальная установка и методика измерений
| Рис. 9.4. Схема экспериментальной установки |
 Схема экспериментальной установки приведена на рис. 9.4 к штативу 4 крепится кронштейн с электромагнитным вибратором 3, с помощью которого в струне 1 возбуждаются синусоидальные колебания от звукового генератора. Если нагрузить струну и включить звуковой генератор, от вибратора по струне побегут поперечные волны, которые, отражаясь от концов, образуют сложную картину колебаний. Медленно изменяя частоту звукового генератора, можно заметить, что колебания струны при некоторых частотах стабилизируются – появляются стоячие волны. При этом струна делится неподвижными узлами на несколько равных отрезков. Амплитуда колебаний отдельных точек струны не зависит от времени и определяется только их положением на струне. При изменении нагрузки картина немедленно размывается. Меняя частоту генератора, можно вновь получить стоячую волну с тем же числом узлов.
Схема экспериментальной установки приведена на рис. 9.4 к штативу 4 крепится кронштейн с электромагнитным вибратором 3, с помощью которого в струне 1 возбуждаются синусоидальные колебания от звукового генератора. Если нагрузить струну и включить звуковой генератор, от вибратора по струне побегут поперечные волны, которые, отражаясь от концов, образуют сложную картину колебаний. Медленно изменяя частоту звукового генератора, можно заметить, что колебания струны при некоторых частотах стабилизируются – появляются стоячие волны. При этом струна делится неподвижными узлами на несколько равных отрезков. Амплитуда колебаний отдельных точек струны не зависит от времени и определяется только их положением на струне. При изменении нагрузки картина немедленно размывается. Меняя частоту генератора, можно вновь получить стоячую волну с тем же числом узлов.
Последовательность выполнения работы
1. Влючите звуковой генератор и дайте ему прогреться в течение 5 минут. Установите частоту генератора на 0.
2. Нагрузите струну и изменением частоты генератора получите стоячие волны для нескольких значений числа пучностей n = 1, 2, 3,… при фиксированном значении нагрузки. Все измерения повторите 3–4 раза.
3. Повторите измерения по п. 2 с другими значениями нагрузки. Число различных значений нагрузки должно быть не менее пяти.
4. Изменяя частоту звукового генератора при некотором постоянном натяжении струны, получите стоячие волны, соответствующие различным n. Повторите процесс измерения не менее трех раз.
5. Проделайте измерения по п. 4 для различных значений натяжения струны (не менее пяти значений).
Обработка результатов эксперимента
1. По измерениям п. 2 постройте график зависимости 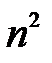 от
от 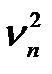 при различных натяжениях струны F. Методом наименьших квадратов найдите тангенсы угла наклона прямых к оси абсцисс и погрешность определения тангенсов.
при различных натяжениях струны F. Методом наименьших квадратов найдите тангенсы угла наклона прямых к оси абсцисс и погрешность определения тангенсов.
2. Найдите линейную плотность струны по формуле
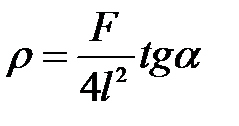 .
.
3. Найдите погрешность косвенного измерения линейной плотности струны по формуле
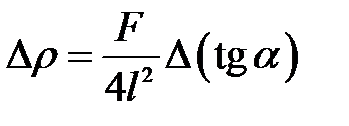 .
.
4. Систематическую погрешность, связанную с измерением длины струны, рассчитайте по формуле
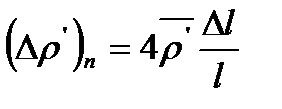 .
.
5. Суммарную погрешность измерения линейной плотности рассчитайте по формуле
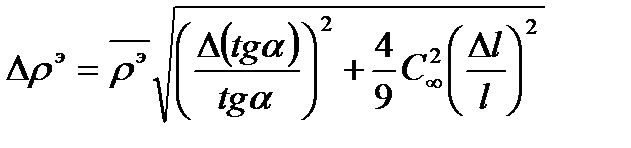 .
.
6. По измерениям п. 2 построить графики зависимости 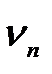 от n при различных натяжениях струны F. Методом наименьших квадратов найти тангенсы угла
от n при различных натяжениях струны F. Методом наименьших квадратов найти тангенсы угла 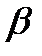 наклона прямых к оси абсцисс и погрешность определения тангенсов.
наклона прямых к оси абсцисс и погрешность определения тангенсов.
7. Найдите скорость распространения волны при данном натяжении по формуле
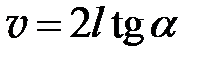 .
.
8. Найдите погрешность определения скорости по формуле:
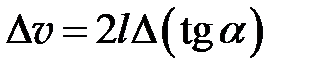 .
.
9. Систематическую погрешность, связанную с измерением длины струны рассчитайте по формуле
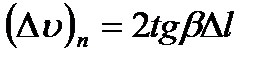 .
.
10. Суммарную погрешность измерения скорости рассчитайте по формуле
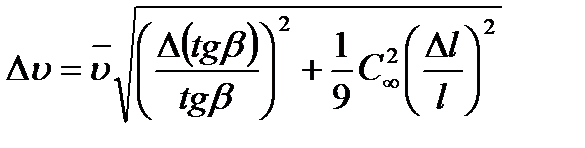 .
.
11. По измерениям п. 4 проверьте выполнение соотношения
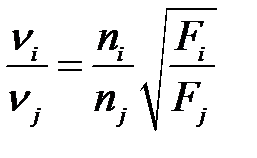 .
.
Вязкость жидкости
Явление внутреннего трения (вязкости) наблюдается в телах во всех агрегатных состояниях, но большое практическое значение это имеет для жидкостей и газов.
При движении жидкости или газа возникают силы внутреннего трения. Эти силы возникают вследствие того, что движение жидкости или газа слоистое, и скорости перемещающихся слоев разные.
Представим себе две пластинки, разделенные плоскопараллельным слоем жидкости. Рассмотрим, что произойдет, если сначала перемещать верхнюю пластинку относительно нижней в направлении, указанном стрелкой. Мысленно разобьем жидкость на тончайшие слои. Молекулы жидкости, ближайшие к верхней пластинке, прилипают к ней и в силу этого начинают перемещаться вместе с пластинкой с той же скоростью. Эти молекулы в свою очередь увлекают молекулы следующего слоя и так далее Слой молекул, непосредственно прилегающих к нижней неподвижной пластине, остается в покое, а остальные слои перемещаются, скользя друг по другу со скоростями тем большими, чем больше их расстояние от нижнего слоя.
Силы внутреннего трения направлены к уравниванию скорости движения всех слоев. Уравнивание скорости слоев осуществляется путем передачи молекулами более быстрого слоя количества движения mυ молекулам слоя, движущегося медленнее. Это приводит к увеличению скорости движения движущийся быстрее слой, начинает двигаться медленнее, так как молекулы из медленного слоя, попадая в более быстрый слой, получают в быстром слое некоторое количество движения, что приводит к его торможению.
Таким образом, внутреннее трение обусловлено переносом количества движения веществ mυ молекулами вещества, которые переходят из слоя в слой и создают возникновение сил трения между слоями газа или жидкости, перемещающимися параллельно друг другу с различными скоростями.
Опыт показал, что сила внутреннего трения F пропорциональна величине площади соприкосновения движущихся слоев S, градиенту скорости движения слоев, коэффициенту пропорциональности η, который называется коэффициентом вязкости (закон Ньютона):
 . (10.1)
. (10.1)
| V |
| х |
| V2 |
| V1 |
| dx |
| X |
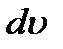 Градиентом скорости
Градиентом скорости 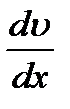 называется изменение скорости dυ на единицу длины dx в направлении, перпендикулярном движению слоев (рис.10.1). Коэффициент вязкости
называется изменение скорости dυ на единицу длины dx в направлении, перпендикулярном движению слоев (рис.10.1). Коэффициент вязкости
| Рис. 10.1. Схема внутреннего трения |
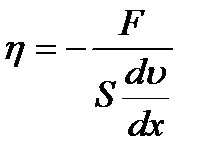 . (10.2)
. (10.2)
Коэффициент вязкости, или коэффициент внутреннего трения, есть физическая величина, численно равная силе внутреннего трения, между двумя слоями с площадью, равной единице при градиенте скорости, равном единице. В СИ [η] кг/(м∙сек).
Знак минус в формуле Ньютона показывает, что сила F направлена противоположно изменению скорости.
В некоторых случаях вместо определенной выше динамичской вязкости удобнее пользоваться кинематической вязкостью — отношениемдинамической вязкости η к плотности ρ жидкости или газа: 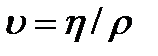 . Иногда вязкость растворов характеризуют относительной вязкостью— отношением вязкости раствора к вязкости растворителя. Приборы, служащие для измерения вязкости, называют вискозиметрами. Вязкость жидкостей зависит от температуры: она резко уменьшается с повышением температуры; особенно сильно зависит от температуры вязкость масел. Так, например, вязкость касторового масла при изменении температуры от 18 до 40оС падает почти в четыре раза.
. Иногда вязкость растворов характеризуют относительной вязкостью— отношением вязкости раствора к вязкости растворителя. Приборы, служащие для измерения вязкости, называют вискозиметрами. Вязкость жидкостей зависит от температуры: она резко уменьшается с повышением температуры; особенно сильно зависит от температуры вязкость масел. Так, например, вязкость касторового масла при изменении температуры от 18 до 40оС падает почти в четыре раза.
Теперь установим выражение для коэффициента вязкости 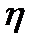 через молекулярные характеристики. Для этого выведем общее уравнение переноса. Рассмотрим молекулы, которые проходят через поперечное сечение S в точке x, двигаясь слева и справа,
через молекулярные характеристики. Для этого выведем общее уравнение переноса. Рассмотрим молекулы, которые проходят через поперечное сечение S в точке x, двигаясь слева и справа, 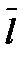 − средняя длина свободного пробега молекул (рис. 10.2). В поперечном сечении
− средняя длина свободного пробега молекул (рис. 10.2). В поперечном сечении 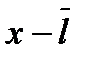 и
и 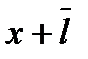 молекулы испытывают последнее столкновение перед пролетом сквозь сечение S. Поэтому концентрации молекул n и их скорости диффузии
молекулы испытывают последнее столкновение перед пролетом сквозь сечение S. Поэтому концентрации молекул n и их скорости диффузии  в обоих объемах слева и справа от x неизменны и такие же, как в сечениях
в обоих объемах слева и справа от x неизменны и такие же, как в сечениях 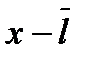 и
и 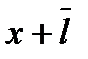 . За промежуток dt слева через сечение S проходит количество молекул
. За промежуток dt слева через сечение S проходит количество молекул 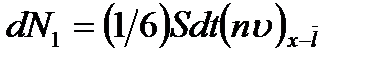 , а справа
, а справа 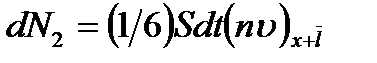 . Множитель
. Множитель  появляется за счет того, что у каждой молекулы шесть степеней свободы, то есть шесть возможных направлений, и по направлению к стенке S летит только их шестая часть.
появляется за счет того, что у каждой молекулы шесть степеней свободы, то есть шесть возможных направлений, и по направлению к стенке S летит только их шестая часть.
Результирующий поток молекул в направлении оси ох определяется как разность: 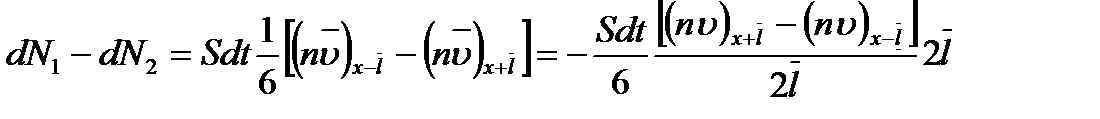 .
.
| z |
| S |
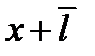
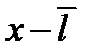
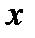
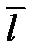
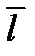
| dN1 |
| dN2 |
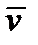
| Рис. 10.2 Общая картина движения молекул в жидкости |
В предельном случае при  , стремящемся к нулю, получим
, стремящемся к нулю, получим 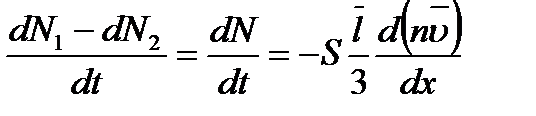 и, следовательно, общее уравнение переноса запишется следующим образом:
и, следовательно, общее уравнение переноса запишется следующим образом:
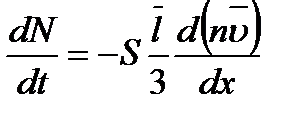 . (10.3)
. (10.3)
При внутреннем трении перпендикулярно к направлению диффузии молекулы получают добавочную скорость 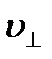 и, следовательно, приобретают добавочный импульс
и, следовательно, приобретают добавочный импульс 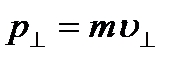 . Для суммарного потока импульса имеем
. Для суммарного потока импульса имеем  . Так как по второму закону Ньютона
. Так как по второму закону Ньютона 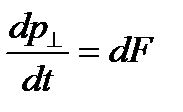 , то получим
, то получим 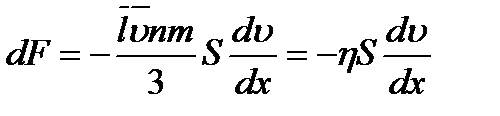 , откуда находим выражение для вязкости
, откуда находим выражение для вязкости 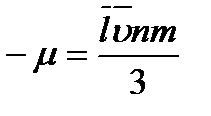 .
.
Определение коэффициента внутреннего трения маловязких жидкостей (глицерин, касторовое масло) методом Стокса.
Коэффициент вязкости может быть определен методом падающего шарика в вязкой среде — методом Стокса.
Стокс установил, что сила внутреннего трения, действующая на шарик радиусом r, движущийся со скоростью υ в жидкости, определяется по формуле
F=6πηrυ.
На шарик, свободно падающий в жидкости, действуют силы тяжести (Р), выталкивающая (Q), и вязкого сопротивления (F) (рис. 10.3):
P=mшg=4/3πr3ρшg,
Q=mжg=4/3πr3ρжg,
F=6πηrυ,
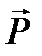
|
| А |
| В |
| l |
| Рис. 10.3. Схема установки |
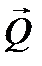 
|
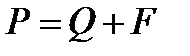 ;
; 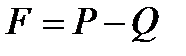 .
.
Или
6πηrυ=4/3πr3g(ρш-ρж),
откуда
 . (10.4)
. (10.4)
Для средней части сосуда, ограниченной рисками А и В, где движение равномерное, скорость равна
υ= l / t,
где l — расстояние, t — время падения шарика между рисками А и В.
Подставляя значение скорости в уравнение (10.2), получим
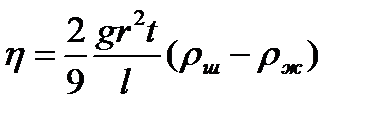 , (10.5)
, (10.5)
Строго говоря, соотношение (10.5), , справедливо лишь тогда, когда шарик падает в безграничной среде. Если шарик падает вдоль оси трубки радиусом R, в (10.4) необходимо ввести поправку, учитывающую наличие стенок трубки. У стенок исследуемая жидкость покоится, а пограничный слой жидкости около шарика движется вместе с ним. Это приводит к увеличению градиента скорости, и, следовательно, скорость равномерного падения шарика в трубке будет меньше, чем в безграничной среде. Учет этого обстоятельства приводит к следующему выражению:
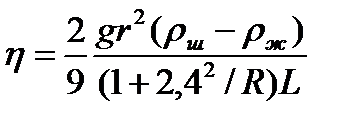 . (10.6)
. (10.6)
Описание экспериментальной установки
Вискозиметр для определения вязкости по методу Стокса представляет собой стеклянный цилиндрический сосуд (рис. 10.3), наполненный исследуемой жидкостью, и с двух сторон закрытый крышками. На цилиндре нанесены две горизонтальные метки А и В, расположенные на расстоянии l. Диаметр шариков измеряется микрометром. Измерив диаметр шарика, его опускают в жидкость как можно ближе к оси трубки. В момент прохождения шариком верхней метки пускают в ход секундомер, а в момент прохождения шариком нижней метки секундомер останавливают. Опыт проводят 5−7 раз.
Обработка результатов
1. Скорость равномерного движения шарика 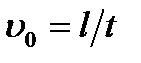 , поэтому коэффициент вязкости можно рассчитать по формуле
, поэтому коэффициент вязкости можно рассчитать по формуле
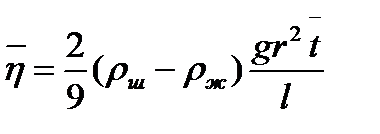 , (10.7)
, (10.7)
где 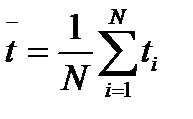 . (10.8)
. (10.8)
2. Погрешность величины t определить по методике расчёта погрешностей прямых многократных измерений, задавая доверительную вероятность 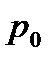 и коэффициент Стьюдента.
и коэффициент Стьюдента.
3. Погрешность косвенных измерений величины 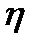 вычислить по формуле
вычислить по формуле
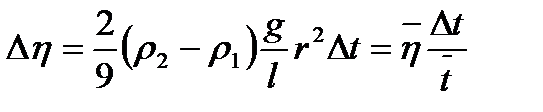 . (10.9)
. (10.9)
4. Результат представить в виде 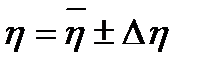 .
.
5. Если измерение проводится один раз, и при этом измеряются все три величины l, r и t, входящие в формулу 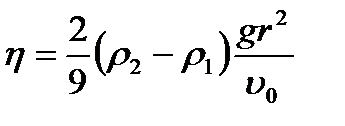 , то приборную погрешность необходимо рассчитать по формуле
, то приборную погрешность необходимо рассчитать по формуле
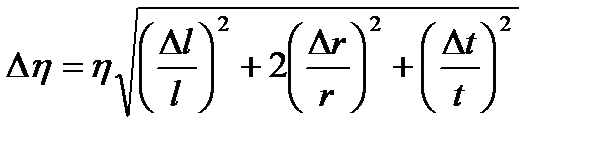 . (10.10)
. (10.10)
6. Результат представить в виде: 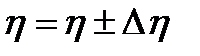 .
.
Возможны различные другие варианты, при которых предварительно оцениваются погрешности измеряемых величин и не учитываются в конечном результате, если они малы. Но все эти варианты являются частными случаями рассмотренных.
Дата добавления: 2015-09-25; просмотров: 958;
