Теорема Бура об абсолютной и относительной производных любого вектора по времени

Выясним вопрос о том, как вычислять производные векторов, заданных в проекциях на оси подвижных координат. Пусть задан вектор

(50)

в подвижных осях.

Тогда

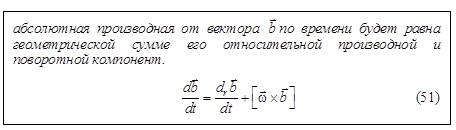
Доказательство. Вычислим эту производную непосредственно. Тогда

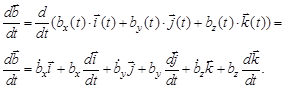
Здесь возникает вопрос о том, какое движение совершают концы единичных векторов и каким образом можно вычислить производные от них?

Во первых, скорости концов этих векторов перпендикулярны самим векторам по теореме о производной от единичного вектора по параметру. Ясно, что они совершают вращательное движение с угловой скоростью 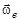вокруг мгновенной оси, проходящей через точку С. А раз так, то эти производные можно вычислить по формуле Эйлера.

Тогда

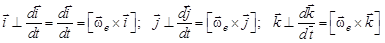
и

.

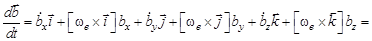
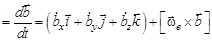Или в компактной форме записи:

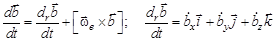. (52)