Общая постановка задачи о сложном движении точки

В физических основах механики выделяют инерциальные и неинерциальные системы отсчета. Рассмотрим движение точки М по отношению к двум таким системам координат, представленным на рис. 41. Задачу представим как задачу о наведении перехватчика на бомбардировщик противника.

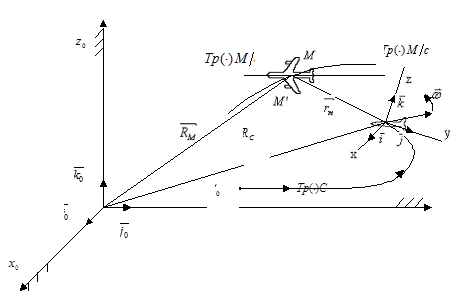Рис. 41

В соответствии с аксиомами классической кинематики (евклидовой геометрии) запишем для точки М:

;

;

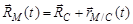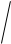
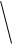
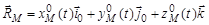
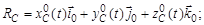
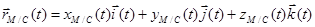(49)

В соответствии с научной традицией будем все абсолютные величины помечать индексом «а»: .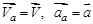

Все относительные величины будем помечать индексом «r» (от французского слова relative – относительный): .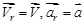

Заметим, что абсолютная и относительная траектории существуют объективно, и мы можем о них говорить.

В соответствии с научной традицией будем все переносные величины обозначать индексом «е»: .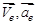

Так как в каждый момент времени движущаяся точка М проходит через разные точки М΄ подвижного пространства, которые движутся по разным траекториям относительно неподвижных осей, то говорить о переносной траектории, о ее существовании не имеет смысла. Можно лишь говорить об элементе переносной траектории, связанном с вектором 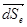в данный момент времени. В целом движение системы координат 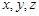относительно системы координат 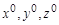можно представить как движение подвижного пространства сквозь неподвижное.