Построение плоских фигур.
| · Построение треугольника АВС по трем отрезкам m, n, и p (рис. 2.16). На произвольной прямой откладывают отрезок АВ = n. Из точки А как из центра описывают дугу радиусом R1 = m, а из точки В – дугу радиусом R2 = p до взаимного их пересечения в точке С. Найденную точку С соединяют с точками А В. | 
Рис. 2.16
|
· Построение многоугольника, равного данному (рис. 2.17, 2.18). Это построение можно выполнить двумя способами:
| 1.Способ (триангуляции). Из точки А (рис. 2.17) проводят диагонали, делящие многоугольник на треугольники. Искомый многоугольник строят поэтапно как ряд последовательных треугольников по трем отрезкам способом, показанным на рис. 2.16. | 
Рис. 2.17
|
2. Способ (координатный). Положение любой точки на плоскости может быть задано ее координатами, например точки А (рис. 2.19), определяется ее координатами ХА и YА. На нижнем рисунке изображено упрощенное построение точки А по ее координатам ХА и YА. На рис. 2.18 показано построение многоугольника А1В1С1D1Е1 равному многоугольнику АВСDЕ по координатам.
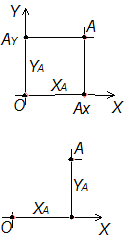Рис. 2.19
|
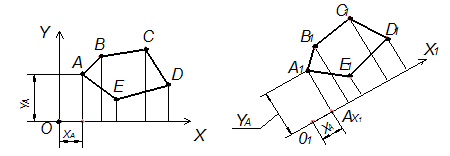Рис. 2.18
|
Дата добавления: 2015-09-25; просмотров: 1087;