Функция распределения микросостояний фазового ансамбля
Точка X фазового пространства описывает микросостояние системы. В бесконечно малом безразмерном объеме
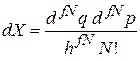
около точки X вероятность реализации микросостояния равна 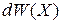 . Вероятность реализации в единичном объеме около точки X называется функцией распределения, или плотностью вероятности
. Вероятность реализации в единичном объеме около точки X называется функцией распределения, или плотностью вероятности
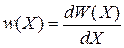 . (2.3)
. (2.3)
Вероятность нахождения системы в интервале 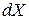
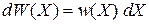 (2.3а)
(2.3а)
удовлетворяет условию нормировки
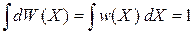 , (2.4)
, (2.4)
где интегрирование ведется по всему фазовому пространству. Среднее значение по фазовому ансамблю величины 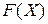 , зависящей от микроскопических переменных X,равно
, зависящей от микроскопических переменных X,равно
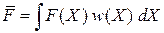 . (2.4а)
. (2.4а)
Задача статистической физики состоит в том, чтобы для фиксированного макросостояния найти функцию распределения микросостояний по фазовому пространству 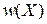 .
.
Эргодическая гипотеза утверждает, что среднее по фазовому ансамблю равно среднему по времени. Если приготовить множество одинаковых систем в одном и том же макроскопическом состоянии и найти среднее по их микросостояниям в один момент времени, то результат совпадает с усреднением по микросостояниям, которые принимает одна системы с течением времени. Следовательно, усреднение по фазовому ансамблю и по фазовой траектории дают одинаковый результат.
Плотность вероятности 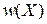 пропорциональна числу реализованных микросостояний в единице объема фазового пространства, т. е. плотности микросостояний. Установим общие свойства
пропорциональна числу реализованных микросостояний в единице объема фазового пространства, т. е. плотности микросостояний. Установим общие свойства 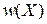 , используя теорему Лиувилля.
, используя теорему Лиувилля.
Дата добавления: 2015-09-21; просмотров: 971;
