Элемент объема фазового пространства равен

.

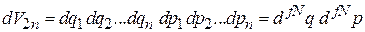При 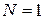, , 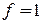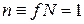единица измерения

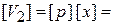кг·м²/с = Дж·с ,

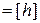где h – постоянная Планка. Микрочастицы – молекулы, атомы, электроны подчиняются законам квантовой механики. Микрочастицы одной природы тождественны друг другу. Теорема о частотной полосе для сопряженных переменных в преобразовании Фурье 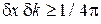в квантовой механике называется соотношение неопределенностей Гейзенберга

.

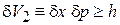Это ограничивает снизу фазовый объем микросостояния с 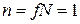. Тогда в 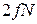-мерном фазовом пространстве минимальный объем микросостояния 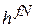. В результате в элементе объема 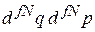находится число физически различных микросостояний

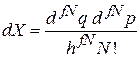, (2.2)

что является безразмерным элементом фазового объема. Множитель N! учитывает тождественность микрочастиц – их взаимная перестановка дает N! физически одинаковых состояний, которые должны учитываться однократно.

Число микросостояний, которое может быть в объеме 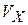фазового пространства, получаем из (2.2)

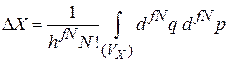. (2.2а)

Для конкретного макросостояния не все микросостояния реализуются с одинаковой вероятностью. Степень их реализации описывает функция распределения.

При отсутствии внешнего поля координаты и импульсы частиц не связаны между собой и интегрирования в (2.2а) разделяются

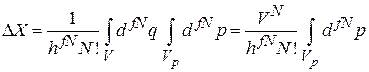, (2.2б)

где V – объем координатного пространства, то есть объем сосуда с газом; 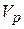– объем импульсного пространства, доступный для частиц газа.