Число степеней свободы
Число степеней свободы системы n равно сумме степеней свободы составляющих частиц. Если есть N одинаковых независимых частиц и у каждой f степеней свободы, то
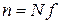 .
.
Число степеней свободы частицы f есть число независимых координат, определяющих ее положение в пространстве. Изменение координаты означает движение, тогда f – число независимых видов движения.
Атом, рассматриваемый как материальная точка, имеет в трехмерном пространстве декартовые координаты (x,y,z) и 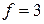 . Изменение координат дает три независимых поступательных движения вдоль взаимно перпендикулярных осей. Вращательное движение не изменяет координат.
. Изменение координат дает три независимых поступательных движения вдоль взаимно перпендикулярных осей. Вращательное движение не изменяет координат.
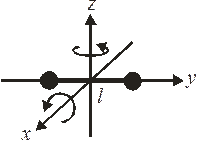
Двухатомная молекула. Два атома имеют 6 координат. Если между атомами жесткая связь длиной l, тогда координаты связаны теоремой Пифагора – уравнением
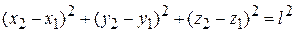 .
.
Независимыми являются 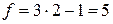 координат. Их изменение дает 3 поступательных и 2 вращательных движения вокруг осей x и z. Вращение вокруг оси y не изменяет координаты атомов и не связано с затратой энергии.
координат. Их изменение дает 3 поступательных и 2 вращательных движения вокруг осей x и z. Вращение вокруг оси y не изменяет координаты атомов и не связано с затратой энергии.
Если связь между атомами упругая, то атомы колеблются относительно друг друга, и добавляются 2 степени свободы, связанные с кинетической и потенциальной энергиями колебаний, в результате 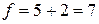 .
.
N-атомная молекула 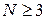 . Атомы имеют
. Атомы имеют 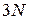 координат, часть из них зависит друг от друга благодаря связям между атомами. В число степеней свободы молекулы дают вклады:
координат, часть из них зависит друг от друга благодаря связям между атомами. В число степеней свободы молекулы дают вклады:
независимые поступательные движения молекулы вдоль декартовых осей x, y, z;
независимые вращения вокруг трех декартовых осей.
В результате для жестких связей 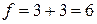 .
.
Остальные координаты блокированы связями между атомами, число блокированных связей 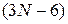 .
.
Если все связи упругие, то на каждую приходится по две степени свободы, в результате
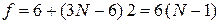 .
.
Например, для 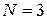 получаем
получаем 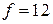 .
.
Дата добавления: 2015-09-21; просмотров: 1152;
