Основные положения. Объект– идеальный газ независимых микрочастиц, подчиняющихся классической механике и описываемых уравнениями Гамильтона
КЛАССИЧЕСКАЯ СТАТИСТИЧЕСКАЯ ФИЗИКА
Объект– идеальный газ независимых микрочастиц, подчиняющихся классической механике и описываемых уравнениями Гамильтона. Эти уравнения являются законами динамики, записанными через гамильтониан – полную энергию, выраженную через координаты и импульсы частиц. Выбор этих переменных вызван тем, что микрочастицы подчиняются законам квантовой физики. Неопределенности координат и импульсов частицы связаны соотношением Гейзенберга 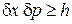 , что существенно используется при статистическом описании даже в рамках классической физики. Используется также тождественность микрочастиц.
, что существенно используется при статистическом описании даже в рамках классической физики. Используется также тождественность микрочастиц.
Задача– найти статистические распределения частиц газа по координатам, импульсам, энергии. Используется метод Гиббса, разработанный в 1902 г.

Джозайя Уиллард Гиббс (1839–1903)
Основные понятия: микросостояние газа, макросостояние газа, фазовое пространство, функция распределения по фазовому пространству.
Микросостояние системы частиц – совокупность координат и импульсов всех частиц газа, зафиксированных в один момент времени. Микросостояние отображает точка X в фазовом пространстве. С течением времени микросостояние изменяется и точка перемещается по фазовому пространству.
Функция распределения плотности вероятности 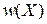 – вероятность обнаружения микросостояния газа в единице объема фазового пространства около точки X.
– вероятность обнаружения микросостояния газа в единице объема фазового пространства около точки X.
Статистический интегралZ– нормировочная постоянная функции распределения.
Макросостояние системы частиц – состояние газа как единого целого. Описывается термодинамическими величинами – температурой Т, давлением Р, внутренней энергией U, свободной энергией F и др. Одно макросостояние реализуется множеством разных микросостояний, образующих фазовый ансамбль. Термодинамическая величина, характеризующая макросостояние, получается усреднением по фазовому ансамблю с использованием функции распределения, и выражается через статистический интеграл Z.
Дата добавления: 2015-09-21; просмотров: 664;
