Объем и площадь n-мерной сферы
На основании размерности для объема n-мерной сферы радиусом r, для объема шарового слоя толщиной dr и для площади сферы получаем
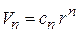 ,
,
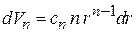 ,
,
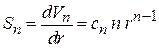 .
.
Найдем постоянную 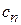 , вычислив сходящийся интеграл
, вычислив сходящийся интеграл
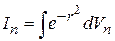
по всему пространству в декартовых и сферических координатах.
В декартовых координатах
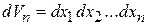 ,
,
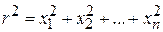 ,
,
тогда
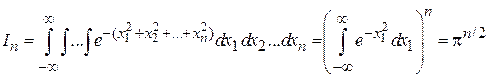 ,
,
где использован интеграл Пуассона (доказывается в курсе ММФ)
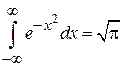 .
.
В сферических координатах
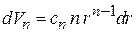 ,
,
тогда
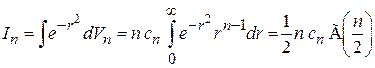 ,
,
где использовано
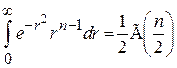 .
.
Гамма-функция вычисляется по формулам
Г(n + 1) = n!, 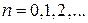 ,
,
Г(z + 1) = z Г(z),
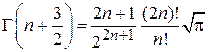 ,
,
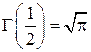 ,
, 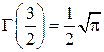 ,
, 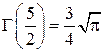 ,
,
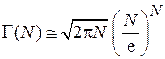 при
при 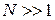 .
.
Сравниваем результаты в декартовых координатах
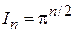
и в сферических координатах
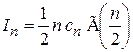 ,
,
находим
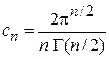 .
.
В результате объем n-мерного шара, шарового слоя и площадь сферы
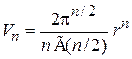 , (П.2.1)
, (П.2.1)
 . (П.2.2)
. (П.2.2)
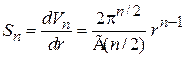 . (П.2.3)
. (П.2.3)
В частности при 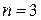 с учетом
с учетом 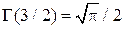 получаем известные из школы соотношения
получаем известные из школы соотношения
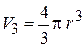 ,
, 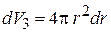 ,
, 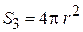 .
.
Эллипсоид с полуосями 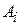 удовлетворяет уравнению
удовлетворяет уравнению
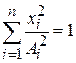 .
.
Сравниваем с уравнением сферы
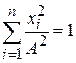 ,
,
обобщаем (П.2.1)
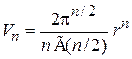 ,
,
находим объем n-мерного эллипсоида
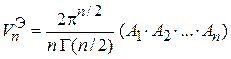 . (П.2.1а)
. (П.2.1а)
Дата добавления: 2015-09-21; просмотров: 4456;
