Связи и их классификация
При изучении динамики несвободной материальной точки мы уже рассматривали связи. Обобщим эти понятия на систему материальных точек.
Механическая система называется свободной, если ее точки могут занимать любые положения, а их скорости могут принимать произвольные значения. В противном случае механическая система называется несвободной. Для несвободных систем должны быть указаны ограничения, накладываемые на координаты или скорости или на те и другие. Эти ограничения, как мы знаем, называются связями. Они могут быть записаны в виде уравнений или неравенств.
В общем случае уравнение связи можно записать в виде:

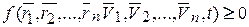 или
или
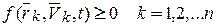 (16.1)
(16.1)
Если в соотношении (16.1) реализуется только знак равенства, то связь называется удерживающей, если в виде неравенства, то – неудерживающей. Если уравнение связи не содержит скорости точек, т.е.
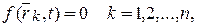 то (16.2)
то (16.2)
связь называется геометрической или голономной.
Если же в уравнение связи входят скорости точек, то связь называется кинематической или дифференциальной. Если уравнение кинематической связи нельзя проинтегрировать и нельзя представить в виде (16.2), то такая связь называется неголономной.
Пример 1. Гантель (рис. 16.1).
Две материальные точки связанные невесомым стержнем называются «гантелью». Пусть длина стержня равна l.
 Рис. 16.1
Рис. 16.1
| Тогда координаты материальных точек удовлетворяют уравнению геометрической связи:
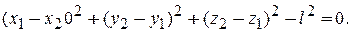
|
Пример 2. Кривошипно-ползунный механизм (рис. 16.2).
 Рис.16.2
Рис.16.2
| Рассмотрим механизм как систему связанных материальных точек А и В.
Уравнения связей:
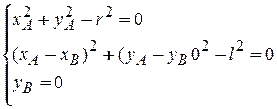
|
Дата добавления: 2015-09-21; просмотров: 691;
