Виртуальные перемещения

Рассмотрим простейший случай. Пусть материальная точка находится на стационарной поверхности, т.е. на поверхности, которая с течением времени не изменяется.

Определение: Назовем виртуальными перемещения точек в рассматриваемом случае всякие бесконечно малые ее перемещения поповерхности.

Получим условия для таких перемещений.

Уравнение поверхности является уравнением связи

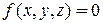(16.3)

Пусть 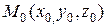начальное положение материальной точки на поверхности, определяемое радиус-вектором 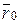(рис.16.4). Рассмотрим любое малое перемещение точки 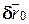по поверхности, не нарушающее связи координатами нового положения точки будут

,

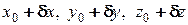где 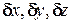- проекции вектора .

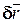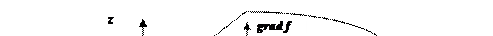
Рис.16.4

Подставим эти координаты в уравнение связи:

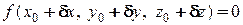(16.4)

Разложим выражение (16.4) в ряд по степеням :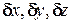

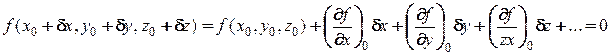
Ограничимся первым порядком малости, удерживая только линейные члены

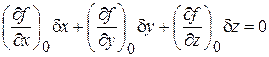(16.5)

Таким образом, виртуальные перемещения должны удовлетворять уравнению (16.5).

Геометрическая интерпретация условия (16.5)

Выражение (16.5) можно переписать в виде:

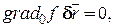(16.6)

где .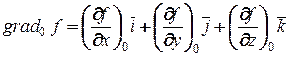

Вывод: Векторы виртуальных перемещений расположены в касательной плоскости (рис.16.4) к поверхности в рассматриваемой точке.