Переменный вектор и его производная по скалярному аргументу

ЛЕКЦИЯ 5

КИНЕМАТИКА ТОЧКИ

Кинематика изучает движение тел по отношению к системам координат, связанных с другими телами (например, с Землей) с геометрической стороны, без учета причин, вызывающих это движение. При этом движение тел предполагается совершающимся во времени.

Для простоты изучения, в кинематике изучается сначала движение одной точки, а затем – движение твердых тел.

Но прежде чем приступить к изучению кинематики точки, рассмотрим понятие производной вектора по скалярному аргументу.

Переменный вектор и его производная по скалярному аргументу

Если каждому значению независимого скалярного переменного u в интервале b < u < c соответствует определенный вектор 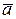, то будем говорить, что вектор 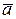есть непрерывная функция скалярного переменного u:

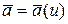. (5.1)

Если вектор 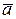при своем изменении сохраняет одно и тоже начало (пусть точка О ) (рис. 5.1), то уравнение (5.1) определяет движение его конца. Кривая, которую описывает конец вектора называется годографом переменного вектора.

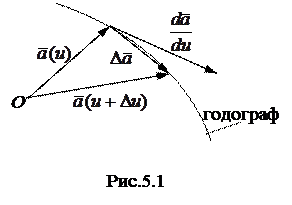Пусть u некоторое фиксированное значение аргумента вектора 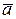, Du – его приращение, тогда при значении

u +Du – будем иметь другой вектор .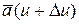

Разность 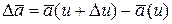называется приращением вектора .

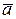Предел отношения

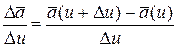
при Du Þ0, если он существует, называется производной вектора 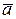по скалярному аргументу u и обозначается

.

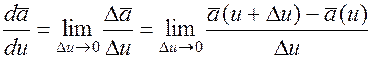Вектор 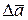всегда направлен по секущей (рис.5.1). При 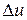Þ0 секущая займет предельное положение, совпадающее с касательной к годографу вектора 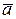. Следовательно, производная вектора по скалярному аргументу всегда направлена по касательной к годографу этого вектора.