Свойства производной вектора по скалярному аргументу
1. 
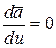, если 
.
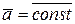2. 
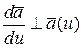, если 
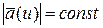, т.е. изменяется только направление вектора в пространстве. Годограф при этом находится на поверхности сферы, а касательная к сфере перпендикулярна ее радиусу.
3. 
.
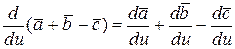4. 
,
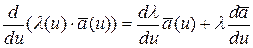где l - скалярный коэффициент.
5. 
.
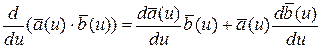6. 
.
 |
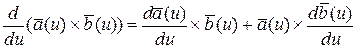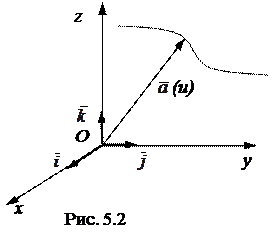Пусть вектор
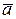задан в неподвижной прямоугольной системе координат, (рис.5.2).
Тогда
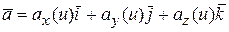, (5.2)
где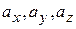 
- проекции вектора 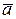на координатные оси, а 
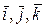- орты этих осей.
Так как 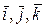- постоянные векторы
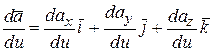. (5.3)
С другой стороны, вектор 
можно также записать через его проекции
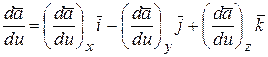. (5.4)
Сравнивая формулы (5.3) и (5.4), получим:
, 
, 
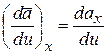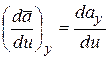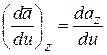. (5.5)
Таким образом, доказали:
Проекция производной вектора на неподвижное направление равна производной от проекции вектора на соответствующее направление.
Перейдем к изучению кинематики точки.
Дата добавления: 2015-09-21; просмотров: 563;