Лекция 9. Тема: Построение планов скоростей и ускорений механизма, образованного группой Ассура 2–го класса 2–го и 3–го видов
Тема: Построение планов скоростей и ускорений механизма, образованного группой Ассура 2–го класса 2–го и 3–го видов. Ускорение Кориолиса.
План лекции.
Построение плана скоростей
Для заданного положения кривошипно-ползунного механизма (план положения механизма построен (рис. 1)) определяются скорости точек графическим методом. Вначале определяем скорость точки A, принадлежащей ведущему звену, которое вращается равномерно с постоянной угловой скоростью w1. Скорость этой точки по модулю равна
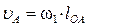
и направлена перпендикулярно оси звена OA в сторону вращения. Отложим от произвольной точки p, называемой полюсом плана скоростей, отрезок (pa). Длину отрезка (pa) выбираем равной (OA). (pa) = (OA) [мм]. Вычисляем масштабный коэффициент скоростей:
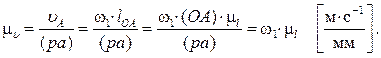
Дезаксиальный кривошипно-ползунный механизм
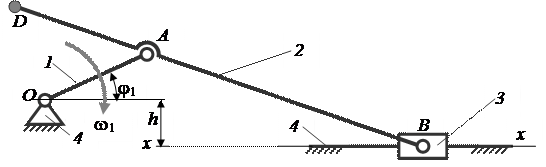 |
Рисунок 1
Строим план скоростей для группы звеньев 2 и 3. Это группа 2–го вида. В состав этой группы входит одна поступательная пара B3 и две последовательно расположенные вращательные пары B2 и A. Звено 2 входит во вращательную пару A со звеном 1, принадлежащим основному механизму, а звено 3 – в поступательную пару B3 со звеном 4, принадлежащим основному механизму. Звено 3 скользит по оси x – x направляющей, принадлежащей звену 4. Обозначим точку B, принадлежащей звену 4, но в данный момент совпадающей с точкой B3, через B4. Тогда воспользуемся известной из теоретической механики теоремой о сложении скоростей для сложного движения точки: абсолютная скорость точки равна геометрической сумме её переносной и относительной скоростей. Определяем скорость точки B по следующим двум векторным уравнениям:
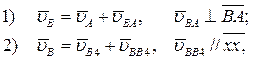
где 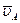 - скорость точки A, нам известная;
- скорость точки A, нам известная; 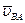 - скорость точки B при вращении звена BA вокруг оси шарнира A, по модулю равная uBA = w2×lBA (w2 – угловая скорость звена BA, которая пока нам неизвестна) и направленная перпендикулярно линии BA;
- скорость точки B при вращении звена BA вокруг оси шарнира A, по модулю равная uBA = w2×lBA (w2 – угловая скорость звена BA, которая пока нам неизвестна) и направленная перпендикулярно линии BA; 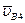 – скорость точки B4 стойки 4, совпадающей с точкой B (она равна нулю, так как звено 4 неподвижно);
– скорость точки B4 стойки 4, совпадающей с точкой B (она равна нулю, так как звено 4 неподвижно); 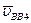 – относительная скорость точки B в её движении относительно точки B4 (её модуль неизвестен, а направлена она вдоль оси xx).
– относительная скорость точки B в её движении относительно точки B4 (её модуль неизвестен, а направлена она вдоль оси xx).
Построение плана скоростей ведём в такой последовательности. Строим решение первого векторного уравнения, указанного выше: из точки a проводим направление скорости изображающий 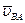 - линию, перпендикулярную BA. Строим решение второго векторного уравнения, указанного выше: из точки p надо было отложить скорость
- линию, перпендикулярную BA. Строим решение второго векторного уравнения, указанного выше: из точки p надо было отложить скорость 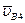 , но она равна нулю, поэтому точку b4 совмещаем с полюсом плана скоростей p; из точки b4 или, что то же, p проводим направление скорости
, но она равна нулю, поэтому точку b4 совмещаем с полюсом плана скоростей p; из точки b4 или, что то же, p проводим направление скорости 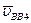 - линию, параллельную xx, до пересечения с линией, проведённой перпендикулярно BA, и получаем точку b - конец вектора скорости точки B. Помещаем в полюс плана точку o (рис. 2). Скорость точки D находим по правилу подобия: конец вектора этой скорости должен лежать на продолжении отрезка (ab). Составляем следующую пропорцию:
- линию, параллельную xx, до пересечения с линией, проведённой перпендикулярно BA, и получаем точку b - конец вектора скорости точки B. Помещаем в полюс плана точку o (рис. 2). Скорость точки D находим по правилу подобия: конец вектора этой скорости должен лежать на продолжении отрезка (ab). Составляем следующую пропорцию:
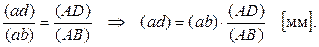
Определяем скорость точки B: uB = (pb)×mu [м/c].
Определяем скорость точки D: uE = (pd)×mu [м/c].
Определяем угловую скорость звена AB:
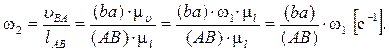
Направление угловой скорости w2 может быть определено следующим образом. Мысленно прикладывая вектор 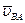 к точке B, видим, что вращение звена 2 вокруг оси шарнира A, принятой за полюс, происходит в направлении, обратном вращению часовой стрелки. Отмечаем направление вращения этого звена в виде дуговой стрелки.
к точке B, видим, что вращение звена 2 вокруг оси шарнира A, принятой за полюс, происходит в направлении, обратном вращению часовой стрелки. Отмечаем направление вращения этого звена в виде дуговой стрелки.
Угловая скорость ползуна 3 равна нулю, так как он движется поступательно относительно неподвижной направляющей: w3 = 0.
Построение плана ускорений
Ускорения точек находятся методом плана ускорений. Строим план ускорений для группы звеньев 2 и 3. Здесь звено 3 движется поступательно относительно направляющей звена 4. Воспользуемся известной из теоретической механики теоремой о сложении ускорений (теорема Кориолиса): при сложном движении ускорение точки равно геометрической сумме трёх ускорений: переносного, кориолисова и относительного. Этот план строится по таким двум векторным уравнениям:
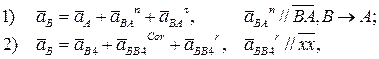
где 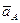 - полное ускорение точки A, равное нормальному ускорению
- полное ускорение точки A, равное нормальному ускорению 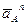 , так как звено 1 (кривошип) вращается равномерно и угловое ускорение равно нулю, следовательно равно нулю и тангенциальное ускорение
, так как звено 1 (кривошип) вращается равномерно и угловое ускорение равно нулю, следовательно равно нулю и тангенциальное ускорение 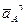 ,
,
aA = aAn = w12×lOA
и направленное параллельно линии OA от точки A к точке O (к центру кривизны траектории);
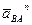 - нормальное ускорение точки B во вращательном движении звена AB вокруг точки A, по модулю равное
- нормальное ускорение точки B во вращательном движении звена AB вокруг точки A, по модулю равное
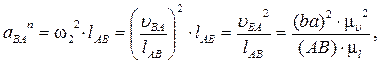
и направленное параллельно линии AB от точки B к точке A ( 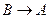 );
);
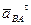 - тангенциальное ускорение точки B в том же движении звена AB, по модулю равное
- тангенциальное ускорение точки B в том же движении звена AB, по модулю равное
aBAt = e2×lAB
(e2 - угловое ускорение звена AB, пока нам неизвестное) и направленное перпендикулярно линии AB;
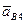 - ускорение точки B4, равное нулю, так как звено 4 неподвижно;
- ускорение точки B4, равное нулю, так как звено 4 неподвижно;
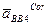 - Кориолисово ускорение точки B в её движении относительно точки B4, равное нулю, так как направляющая (звено 4) не вращается;
- Кориолисово ускорение точки B в её движении относительно точки B4, равное нулю, так как направляющая (звено 4) не вращается;
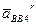 - релятивное ускорение точки B в её движении относительно точки B4, оно направлено параллельно оси xx.
- релятивное ускорение точки B в её движении относительно точки B4, оно направлено параллельно оси xx.
Построение плана ускорений ведём в следующей последовательности. Строим решение первого векторного уравнения, указанного выше, для чего от полюса плана p откладываем отрезок (pa), изображающий ускорение 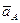 , параллельно линии OA. Длину отрезка (pa) принимаем равной (OA), отчего масштаб ускорений будет
, параллельно линии OA. Длину отрезка (pa) принимаем равной (OA), отчего масштаб ускорений будет
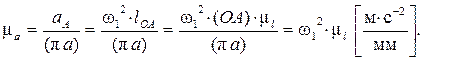
От точки a откладываем отрезок (anBA), изображающий ускорение 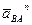 . Длина отрезка (anBA) вычисляется по формуле:
. Длина отрезка (anBA) вычисляется по формуле:
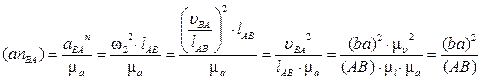 [мм].
[мм].
Через точку nBA проводим направление ускорения 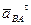 - линию, перпендикулярную линии AB. Переходим к построению решения второго векторного уравнения, указанного выше. Для этого от полюса плана p откладываем вектор ускорения
- линию, перпендикулярную линии AB. Переходим к построению решения второго векторного уравнения, указанного выше. Для этого от полюса плана p откладываем вектор ускорения 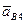 , но оно равно нулю, поэтому точка b4 совпадает с точкой p. С этой же точкой совпадает конец вектора ускорения
, но оно равно нулю, поэтому точка b4 совпадает с точкой p. С этой же точкой совпадает конец вектора ускорения 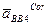 - точка k (ускорение
- точка k (ускорение 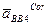 равно нулю). Из точки k или, что то же, из точки p проводим направление ускорения
равно нулю). Из точки k или, что то же, из точки p проводим направление ускорения 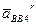 - линию, параллельную xx. Точка пересечения её с линией, проведённой перпендикулярно AB, даёт точку b - конец вектора ускорения точки B. Соединяем точки b и a и получаем вектор полного ускорения точки B при вращении звена AB относительно точки A, т.е.
- линию, параллельную xx. Точка пересечения её с линией, проведённой перпендикулярно AB, даёт точку b - конец вектора ускорения точки B. Соединяем точки b и a и получаем вектор полного ускорения точки B при вращении звена AB относительно точки A, т.е. 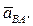 Точку o совмещаем с точкой p (полюсом плана). На этом заканчиваем построение плана ускорений механизма (рис. 3). Конец вектора ускорения точки D найдём по правилу подобия:
Точку o совмещаем с точкой p (полюсом плана). На этом заканчиваем построение плана ускорений механизма (рис. 3). Конец вектора ускорения точки D найдём по правилу подобия:
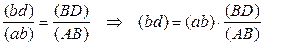 [мм].
[мм].
Соединив точку d с полюсом плана p, получаем отрезок (pd), изображающий абсолютное ускорение точки D.
Величины абсолютных ускорений точек B и D определяются так:
aB = (pb)×ma [м×c – 2];
aD = (pd)× ma [м×c – 2].
Величина углового ускорения звена AB равна:
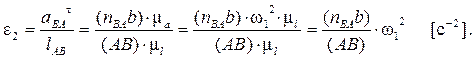
Направление углового ускорения e2 звена 2 (звена AB) может быть определено следующим образом. Перенося мысленно вектор 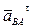 в точку B, видим из точки A, что направление e2 противоположно направлению вращения часовой стрелки. Обозначаем направление углового ускорения e2 на плане положения на соответствующем звене дуговой стрелкой.
в точку B, видим из точки A, что направление e2 противоположно направлению вращения часовой стрелки. Обозначаем направление углового ускорения e2 на плане положения на соответствующем звене дуговой стрелкой.
Угловое ускорение звена 3 (ползуна) равно нулю, так как это звено движется поступательно, e3 = 0.
План скоростей механизма План ускорений механизма
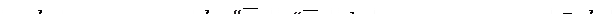
Рисунок 2 Рисунок 3
Рассмотрим механизм, включающий группу 2–го класса 3–го вида. В присоединённой группе средняя кинематическая пара – поступательная, остальные – вращательные (рис. 4). Дано: lOA = 0.05 м, lOC = 0.12 м, lBC = 0.18 м, w1 = 10 c – 1, j1 = 30°.
Механизм Витворта, включающий группу третьего вида

Рисунок 4
Переводим длины звеньев на чертеже в миллиметры и строим план положения механизма. Строим план скоростей механизма. Скорость точки A (пальца кривошипа) известна. Строим план для группы звеньев 2 и 3 по следующим векторным уравнениям:
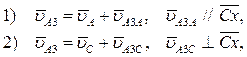
где 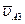 – скорость точки A3 звена 3, которая лежит под точкой A;
– скорость точки A3 звена 3, которая лежит под точкой A; 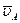 – скорость точки A, по модулю равная uA = w1×lAB = 10×0.05 = 0.5 м×с – 1 и направленная
– скорость точки A, по модулю равная uA = w1×lAB = 10×0.05 = 0.5 м×с – 1 и направленная 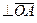 в соответствии с направлением угловой скорости w1;
в соответствии с направлением угловой скорости w1; 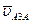 – скорость точки A3 относительно точки A, направленная параллельно линии Cx;
– скорость точки A3 относительно точки A, направленная параллельно линии Cx; 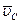 – скорость точки C, равная нулю;
– скорость точки C, равная нулю; 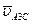 – скорость точки A во вращении звена 3 относительно точки C, по модулю равная uA3C = w3×lA3C и направленная
– скорость точки A во вращении звена 3 относительно точки C, по модулю равная uA3C = w3×lA3C и направленная 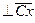 (пока нам не известна).
(пока нам не известна).
Строим решение первого векторного уравнения. От полюса p плана (рис. 5) откладываем отрезок (pa), изображающий скорость 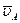 точки A. Длину этого отрезка принимаем равной (pa) = (OA) = 50 мм, т.е. план строим в масштабе кривошипа. Через точку a проводим направление скорости
точки A. Длину этого отрезка принимаем равной (pa) = (OA) = 50 мм, т.е. план строим в масштабе кривошипа. Через точку a проводим направление скорости 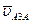 – линию, параллельную Cx. Далее строим решение второго векторного уравнения, указанного выше. Надо отложить вектор скорости точки C, но так как модуль его равен нулю, то конец его c помещаем в полюс плана p и из точки p проводим направление скорости
– линию, параллельную Cx. Далее строим решение второго векторного уравнения, указанного выше. Надо отложить вектор скорости точки C, но так как модуль его равен нулю, то конец его c помещаем в полюс плана p и из точки p проводим направление скорости 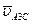 – линию,
– линию, 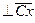 . Пересечение её с ранее проведённой линией, параллельной Cx, даёт конец вектора скорости
. Пересечение её с ранее проведённой линией, параллельной Cx, даёт конец вектора скорости 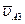 – точку a3. Точку b – конец вектора скорости точки B – находим по правилу подобия из соотношения
– точку a3. Точку b – конец вектора скорости точки B – находим по правилу подобия из соотношения
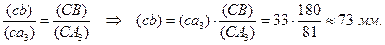
На этом заканчиваем построение плана скоростей механизма Витворта.
План скоростей механизма План ускорений механизма
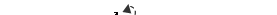

Рисунок 5 Рисунок 6
Масштаб плана скоростей равен
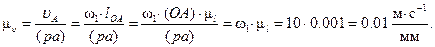
Строим план ускорений группы 2 и 3. Построение ведём по следующим двум векторным уравнениям:
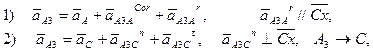
где 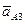 – ускорение точки A3, которая принадлежит звену 3 и совместилась с точкой A звена 1;
– ускорение точки A3, которая принадлежит звену 3 и совместилась с точкой A звена 1; 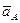 – нормальное (оно же полное) ускорение точки A, по модулю равное
– нормальное (оно же полное) ускорение точки A, по модулю равное
aA = w12×lOA = 102×0.05 = 5 м×с – 2 и направленное параллельно OA от точки A к точке O; aA3ACor – ускорение Кориолиса в движении точки A3 относительно звена 2, по модулю равное
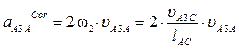
(так как w2 = w3 и w3 = uA3C / lAC) и имеющее направление вектора относительной скорости uA3A, повёрнутого на 90° в направлении угловой скорости w2 переносного движения (движения звена 2); 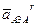 – относительное (релятивное) ускорение точки A3 относительно точки A, направленное параллельно линии Cx;
– относительное (релятивное) ускорение точки A3 относительно точки A, направленное параллельно линии Cx; 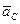 – ускорение точки C (оно равно нулю);
– ускорение точки C (оно равно нулю); 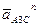 – нормальное ускорение точки A3 во вращении звена 3 относительно точки C, по модулю равное
– нормальное ускорение точки A3 во вращении звена 3 относительно точки C, по модулю равное
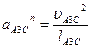
и направленное параллельно линии Cx от точки A3 к точке C; 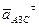 – тангенциальное ускорение точки A3 в том же движении звена 3, по модулю равное aA3Ct = e3×lA3C (нам пока неизвестно) и направленное
– тангенциальное ускорение точки A3 в том же движении звена 3, по модулю равное aA3Ct = e3×lA3C (нам пока неизвестно) и направленное 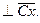
Строим решение первого векторного. Задаёмся отрезком (pa) = (OA) = 50 мм, который изображает в плане ускорение 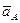 (так как (pa) = (OA), то план строится в масштабе кривошипа).
(так как (pa) = (OA), то план строится в масштабе кривошипа).
Масштаб плана ускорений равен
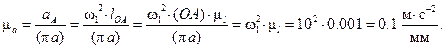
Выбранный отрезок (pa) откладываем от полюса плана (p), далее к нему прибавляем отрезок (ak) – вектор кориолисова ускорения – его длину находим по формуле
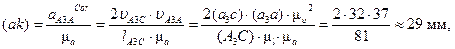
отрезки (a3c) = 32 мм и (a3a) = 37 мм взяты из плана скоростей, а отрезок (A3C) = 81 мм – из плана положения). Через точку k проводим направление ускорения 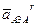 – линию, параллельную Cx.
– линию, параллельную Cx.
Переходим к построению второго векторного уравнения. Точку c совмещаем с точкой p, так как 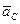 = 0, от точки (p) откладываем отрезок (pnA3C), изображающий нормальное ускорение
= 0, от точки (p) откладываем отрезок (pnA3C), изображающий нормальное ускорение 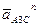 , его длина равна
, его длина равна
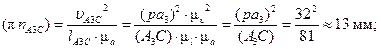
далее через точку nA3C проводим направление ускорения 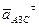 – линию,
– линию, 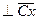 , до пересечения с ранее проведённой через точку k линией, параллельной Cx. Точка пересечения a3 представляет собой конец вектора ускорения
, до пересечения с ранее проведённой через точку k линией, параллельной Cx. Точка пересечения a3 представляет собой конец вектора ускорения 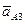 . Конец вектора ускорения центра шарнира B (точку b) найдём по правилу подобия из соотношения
. Конец вектора ускорения центра шарнира B (точку b) найдём по правилу подобия из соотношения
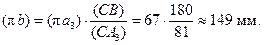
На этом заканчиваем построение плана ускорений механизма Витворта (рис. 6).
Определение кориолисова ускорения
При сложном движении ускорение точки равно геометрической сумме трёх ускорений: переносного, относительного и кориолисова 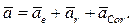
Вектор ускорения Кориолиса определяется по формуле 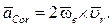 Это удвоенное векторное произведение. Модуль ускорения Кориолиса определяется по формуле
Это удвоенное векторное произведение. Модуль ускорения Кориолиса определяется по формуле 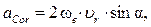 где a – угол между векторами
где a – угол между векторами 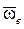 и
и 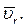
Для определения направления вектора кориолисова ускорения нужно, в общем случае, руководствоваться правилом векторной алгебры (рис.7).
К определению направления ускорения Кориолиса
по правилу векторного произведения
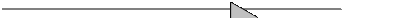
Рисунок 7
Вектор 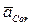 нужно направлять перпендикулярно к плоскости, определяемой векторами
нужно направлять перпендикулярно к плоскости, определяемой векторами 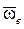 и
и 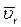 так, чтобы, смотря с конца этого вектора, наблюдатель видел кратчайший поворот от вектора
так, чтобы, смотря с конца этого вектора, наблюдатель видел кратчайший поворот от вектора 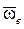 к
к 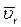 происходящим против хода часовой стрелки.
происходящим против хода часовой стрелки.
К определению направления К определению направления
ускорения Кориолиса в пространственном ускорения Кориолиса в плоском
механизме (угол a ¹ 90°) механизме (угол a = 90° всегда)
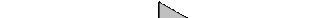 |  |
Рисунок 8 Рисунок 9
На рис. 8 показан другой способ определения направления 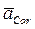 . Здесь u1 = ur sin a представляет собой проекцию
. Здесь u1 = ur sin a представляет собой проекцию 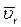 на плоскость перпендикулярную к вектору угловой скорости
на плоскость перпендикулярную к вектору угловой скорости 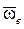 . Поворачиваем эту проекцию на 90° в сторону переносного вращения
. Поворачиваем эту проекцию на 90° в сторону переносного вращения 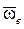 и определяем направление вектора
и определяем направление вектора 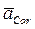 .
.
В случае, если 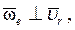 как это имеет место в плоских механизмах, то для определения направления
как это имеет место в плоских механизмах, то для определения направления 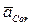 , можно пользоваться весьма простым приёмом, вытекающим из общего правила: чтобы получить направление
, можно пользоваться весьма простым приёмом, вытекающим из общего правила: чтобы получить направление 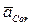 , нужно повернуть вектор
, нужно повернуть вектор 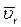 на 90° в направлении переносного вращения (рис. 9). Модуль ускорения Кориолиса в этом случае определяется проще
на 90° в направлении переносного вращения (рис. 9). Модуль ускорения Кориолиса в этом случае определяется проще
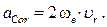
Дата добавления: 2015-09-21; просмотров: 4363;
