Лекция 12. Тема: Приведённые силы и моменты

Тема: Приведённые силы и моменты. Теорема Жуковского. Кинетическая энергия механизма. Приведённая масса и приведённый момент инерции механизма

Приведённые силы и моменты

При исследовании движения механизма, находящегося под действием заданных сил, удобно все силы, действующие на звенья, заменять силами, приложенными к одному из звеньев механизма. Приведённой называют силу, условно приложенную к одной из точек механизма, элементарная работа которой на виртуальном (возможном) перемещении точки приведения равна сумме элементарных работ приводимых сил на перемещениях точек приложения этих сил.

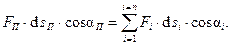(1)

где ds – элементарное перемещение точки приложения силы; a – угол между вектором силы и направлением перемещения точки её приложения.

Разделим равенство (1) на dt:

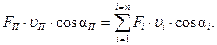(2)

Следовательно,

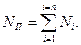(3)

Мощность приведённой силы равна сумме мощностей приводимых сил. Мощность может быть представлена

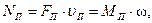(4)

где М_П – приведённый момент пары сил.

Схема звена приведения с приведённой силой и приведённым моментом

Рисунок 1

Теорема Н.Е.Жуковского

Уравновешивающей является сила, равная и направленная противоположно приведённой силе 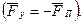Заменяя в уравнении (2) приведённую силу уравновешивающей, получим

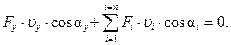(5)

Из уравнения следует, что сумма мощностей на виртуальных перемещениях механизма равно нулю, т.е. получаем аналитическое выражение принципа виртуальных перемещений для данного механизма.

Предположим, что в точке D звена BC приложена сила 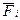(рис. 2, a). Повернём план скоростей звена (рис. 2, b) на 90°; направление поворота может быть произвольным (по вращению часовой стрелки или против, рис. 2, c). В точку D повёрнутого плана перенесём силу 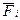и из начала плана (точки p) опустим на направление этой силы перпендикуляр h_i.

Определение уравновешивающей силы с помощью повёрнутого плана скоростей

Рисунок 2

Из рисунка 2, c следует, что

F_i×u_i×cosa_I = F_i×(pd)×m_u×cosa_I = F_i×m_u×h_i = m_u×M_П(F_i), (6)

где m_u – масштаб плана скоростей; F_i×h_i – момент силы F_i относительно полюса плана скоростей.

Следовательно, мощность силы можно представить как момент этой силы относительно начала повёрнутого плана скоростей, умноженный на масштаб плана m_u. Выполнив такую замену в уравнении (5), получим

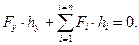(7)

Уравнение (7) выражает теорему Н.Е.Жуковского, являющуюся геометрической интерпретацией принципа виртуальных перемещений: если в соответствующие точки повёрнутого плана скоростей перенести все силы, под действием которых механизм находится в равновесии, то сумма моментов всех этих сил относительно начала плана равна нулю.

Если повёрнутый план рассматривать как жёсткий рычаг с осью вращения в начале плана (рис. 2, c), то уравнение (7) является уравнением равновесия такого рычага.

Согласно принципу Даламбера (Jean d’Alembert), если к механизму, нагруженному внешними силами (движущими или сопротивления), приложены и силы инерции звеньев, то механизм находится в равновесии. Следовательно, если в число сил F_i входят силы сопротивления и силы инерции, то определённая по уравнению (7) уравновешивающая сила F_y будет силой движущей (F_y = F_D). Если эту силу приложить к ведущему звену механизма, то будут преодолены приложенные к нему сопротивления и звенья механизма будут двигаться по заданным законам. Если заданы силы движущие и силы инерции звеньев, то уравновешивающая сила будет силой сопротивления (F_y = R).

На основе принципа независимости действия сил можно, используя теорему Жуковского, определить уравновешивающую для каждой из сил, приложенных к механизму раздельно.

Кинетическая энергия механизма

Уравнение кинетической энергии применительно к механизму имеет вид

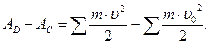(8)

где A_D есть работа всех движущих сил, A_C – работа всех сил сопротивления, 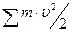– кинетическая энергия механизма, а u₀ и u суть скорости в начале и в конце рассматриваемого перемещения. Можно все движущие силы заменить одной приведённой

Схема звена приведения с приведённой массой

Рисунок 3

силой 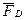, приложенной к выбранному звену приведения AB (рис. 3) в точке B. Точно так же можно все силы сопротивления заменить одной приведённой силой 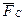, приложенной к тому же звену AB в той же точке B. Моменты сил движущих и сил сопротивления M_D и M_C также можно заменить приведёнными моментами на валу A.

Рассмотрим вопрос о том, как может быть определена кинетическая энергия механизма. В общем случае плоскопараллельного движения звена его кинетическую энергию можно представить в виде суммы энергий в поступательном вместе с центром масс звена и вращательном вокруг его центра масс движениях. Поэтому для механизма можно написать

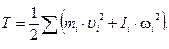(9)

Здесь m_i – масса звена i, u_i – скорость центра масс, I_i – его момент инерции относительно оси, проходящей через центр масс, w_i – его угловая скорость. Рассмотрим, как подсчитывается кинетическая энергия отдельных звеньев в зависимости от вида их движения.

Кинетическая энергия звена, движущегося поступательно, равна

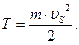(10)

В этой формуле u_S – скорость центра масс звена.

Для звена, совершающего вращательное движение, кинетическая энергия равна

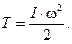(11)

здесь I есть момент инерции звена относительно оси вращения и w – угловая скорость звена.

Для звена, совершающего плоскопараллельное движение, кинетическую энергию можно представить так:

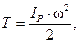(12)

где I_P есть момент инерции звена относительно оси, проходящей через мгновенный центр вращения P, и w – мгновенная угловая скорость звена. Момент инерции I_P относительно оси, проходящей через мгновенный центр вращения, может быть выражен через момент инерции I_S относительно оси, проходящей через центр масс S звена:

I_P = I_S + m×l_PS². (13)

В этом равенстве l_PS есть расстояние от центра масс S звена до мгновенного центра вращения P. Подставляя выражение для I_P из равенства (13) в уравнение (12) и принимая во внимание, что w×l_PS = u_S есть скорость центра масс звена, получаем известную формулу для кинетической энергии звена, имеющего сложное вращательно-поступательное движение:

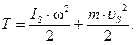(14)

Складывая алгебраически кинетические энергии отдельных звеньев, по формуле (9) получаем значение кинетической энергии всего механизма.

Приведённая масса и приведённый момент инерции механизма

Механизм с одной степенью свободы имеет одно начальное звено, которое может быть выбрано за звено приведения. Пусть механизм состоит из n звеньев, имеет одну степень свободы. В этом механизме выбираем одно звено, например звено AB, в качестве звена приведения, а одну из точек этого звена, например точку B, примем за точку приведения. Звено AB обозначим под номером 1.

Приведённой массой называется такая условная масса, сосредоточенная в точке приведения, кинетическая энергия T_n которой равняется сумме 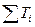кинетических энергий тех звеньев, массы которых приводятся к этой точке. Используем равенство (9). Согласно этому приведённая масса равна

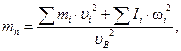(15)

где u_B – скорость точки приведения.

В случае, когда массы звеньев приводятся к звену, совершающему вращательное движение относительно стойки, удобно пользоваться понятием приведённого момента инерции I_n этих масс относительно оси вращения звена приведения.

Приведённый момент инерции равен

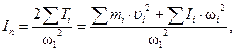(16)

где w₁ – угловая скорость звена приведения. Из равенств (15) и (16) видно, что величина m_n имеет размерность массы [кг], а величина I_n имеет размерность момента инерции [кг×м²]. Из равенства (15) следует, что в общем случае приведённая масса переменна и зависит от квадратов отношений линейных и угловых скоростей, и поэтому она всегда положительна. Аналогично величина I_n в равенстве (16) представляет собой приведённый к звену AB момент инерции звеньев механизма. Это есть момент инерции вращающегося вместе со звеном AB тела, кинетическая энергия которого в каждом рассматриваемом положении механизма равна сумме кинетических энергий всех его звеньев.