Лекция 14. Тема: Механические передачи
Тема: Механические передачи. Цилиндрические зубчатые передачи. Передаточное отношение. Геометрия эвольвентного зацепления. Планетарные и дифференциальные передачи.
Условия работы механизмов, звенья которых имеют вращательное движение, значительно более благоприятны, чем механизмов, звенья которых имеют другие типы движения. Во всех случаях, когда это возможно, стараются все другие типы движения заменить вращательным. При соединении машин-двигателей и рабочих машин в единый агрегат между ними включаются специальные передаточные устройства. Это механические передачи.
Простейшие механизмы для передачи непрерывного вращательного движения включают три звена (ведущее, ведомое и стойку). Если передаточное отношение, которое должно осуществляться механизмом передачи, очень велико или очень мало, то конструктивно удобно между входным и выходным звеньями иметь промежуточные оси с соответствующими звеньями, вращающимися вокруг них. Таким образом, сложный механизм передачи можно разделить на отдельные части – ступени, каждая из которых представляет собой два звена, входящих в высшую пару. Звенья этой пары, кроме того, входят со стойкой в низшие пары. Такая отдельная часть сложного механизма и называется ступенью передачи.
Условимся называть отношение угловой скорости одного звена к угловой скорости другого звена в механизме с одной степенью подвижности передаточным отношением и обозначать буквой u с цифровыми индексами, соответствующими номерам рассматриваемых звеньев. Если оси вращения O1 и O2 параллельны (рис. 1) и заданы постоянные угловые скорости w1 и w2 звеньев 1 и 2, то передаточное отношение u12 равно
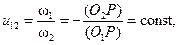 (1)
(1)
где P – мгновенный центр вращения в относительном движении звеньев 1 и 2.
Передача внешнего касания Передача внутреннего касания
 |  |
Рисунок 1 Рисунок 2
Если звенья вращаются в разных направлениях, то передаточное отношение отрицательное; при вращении в одном направлении – положительное. Передачи, обеспечивающие изменения направления вращения ведомого звена (знака передаточного отношения), получили название реверсивных передач. Часто необходимо в процессе работы изменять величину передаточного отношения. Различают передачи со ступенчатым и непрерывным изменением передаточного отношения. Первые называют коробками скоростей, а вторые – вариаторами. По коренным различиям в конструктивном оформлении можно различать:
- передачи, составленные из жёстких тел (звеньев), – фрикционные и зубчатыепередачи;
- передачи, в состав которых, кроме жёстких, входят также и гибкие тела,– ремённые и цепные передачи.
Фрикционные передачи
Фрикционными называют передачи, передающие движение при помощи сил трения, возникающих между катками (звеньями) при наличии нормального давления в точках касания. Их применяют для передачи вращения между параллельными и пересекающимися валами. Чаще применяют фрикционные передачи внешнего касания (рис. 1); реже – передачи внутреннего касания (рис.2).
Если катки (звенья) фрикционной передачи катятся друг по другу без скольжения, то их окружные скорости одинаковы:
u1 = u2; (2)
u1 = w1×r1; u2 = w2×r2.
Следовательно,
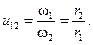 (3)
(3)
Передаточное отношение равно обратному отношению радиусов тел качения.
Расстояние между осями вращающихся валов называют межцентровым расстоянием A. Из рис. 1 и формулы (3) следует:
A = O1O2 = r1 + r2 = r1 + u×r1 = r1 (1 + u); (4)
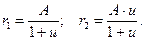 (5)
(5)
Формулы (5) позволяют определить радиусы катков фрикционной передачи по заданным A и u. Передача может быть выполнена с внутренним касанием катков (рис. 2). В этом случае оба вала будут вращаться в одном направлении; радиусы колёс в этом случае равны:
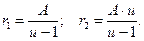 (6)
(6)
Зубчатые передачи
Если на рабочих поверхностях катков фрикционной передачи расположить ряд выступов (зубьев) и впадин так, чтобы зубья одного колеса могли входить во впадины другого, то движение с одного на другой будет передаваться посредством давления в точках касания боковых поверхностей зубьев. Если соответствующим образом выбрать кривые, ограничивающие боковые поверхности зубьев, то можно обеспечить передачу движения с постоянным передаточным отношением.
Катки, на рабочих поверхностях которых расположены зубья и впадины, называются зубчатыми колёсами. Два сцеплённых зубчатых колеса образуют зубчатую передачу. Кривые, ограничивающие боковые поверхности зубьев, называют их профилями; два касающихся друг друга профиля называют сопряжёнными профилями. Оба профиля, как правило, образованы одинаковыми кривыми. Если образующие боковых поверхностей зубьев параллельны оси вращения, то зубья называют прямыми, а передачу – прямозубой. Зубчатые механизмы находят самое широкое применение в машинах и приборах. На рис. 3 показан трёхзвенный зубчатый механизм, состоящий из круглых цилиндрических колёс 1 и 2. Это механизм с внешним зубчатым зацеплением. Угловые скорости w1 и w2 колёс 1 и 2 этого механизма имеют разные знаки. У механизмов с внутренним зубчатым зацеплением угловые скорости w1 и w2 колёс 1 и 2 имеют одинаковые знаки. Окружности радиусов r1, r2 называются начальными окружностями. Профили зубьев подбираются из условия, чтобы нормаль в их точке касания всегда проходила через постоянную точку P – мгновенный центр вращения в относительном движении колёс 1 и 2.
Цилиндрическая зубчатая передача с внешним зацеплением зубьев

Рисунок 3
Передаточное отношение определяется по формуле (3). Практически отношение радиусов удобнее заменять отношением чисел зубьев. Так как расстояние между соседними профилями зубьев сопряжённых колёс должно быть по начальным окружностям одинаковым, то число зубьев z2 на колесе 2 так относится к числу зубьев z1 на колесе 1, как длина начальной окружности колеса 2 относится к длине начальной окружности колеса 1, т.е.
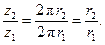
Подставляя полученное выражение в формулу (3), можем написать:
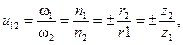 (7)
(7)
где n1 и n2 – частота вращения колёс 1 и 2. Отношение чисел зубьев зубчатых круглых колёс равно обратному отношению угловых скоростей этих колёс. Формула (7) охватывает случай как внешнего зацепления колёс, так и внутреннего.
Частным видом трёхзвенного зубчатого механизма является механизм с реечным зацеплением. Реечное зацепление можно рассматривать как предельный случай любого из
Зубчатая передача с реечным зацеплением зубьев
Рисунок 4
 первых двух, когда радиус одной из начальных окружностей становится бесконечно большим и начальная окружность обращается в начальную прямую. Обычно колесо механизма реечного зацепления имеет реверсивное вращение, а рейка – возвратно-поступательное движение (рис. 4). Колесо 1, вращаясь вокруг оси O1 с угловой скоростью w1, приводит в прямолинейно-поступательное движение рейку 2 со скоростью
первых двух, когда радиус одной из начальных окружностей становится бесконечно большим и начальная окружность обращается в начальную прямую. Обычно колесо механизма реечного зацепления имеет реверсивное вращение, а рейка – возвратно-поступательное движение (рис. 4). Колесо 1, вращаясь вокруг оси O1 с угловой скоростью w1, приводит в прямолинейно-поступательное движение рейку 2 со скоростью 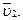 Колесо 1 имеет начальную окружность радиуса r1, а рейка 2 – начальную прямую a – a. Точка P является мгновенным центром вращения в относительном движении звеньев 1 и 2. Скорости w1 и
Колесо 1 имеет начальную окружность радиуса r1, а рейка 2 – начальную прямую a – a. Точка P является мгновенным центром вращения в относительном движении звеньев 1 и 2. Скорости w1 и 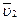 связаны условием
связаны условием
u2 = w1×(O1P) = w1× r1.
К трёхзвенным пространственным механизмам зубчатых передач относятся механизмы конических зубчатых колёс и механизмы червячной передачи с перекрещивающимися под углом 90° осями.
Механизмы многоступенчатых передач
Передаточное отношение, которое можно воспроизвести одной парой зубчатых колёс, невелико. Для осуществления больших передаточных отношений применяются несколько последовательно соединённых колёс, где, кроме входного и выходного, имеются ещё промежуточные колёса, т.е. многоступенчатые передачи. Такие сложные зубчатые механизмы получили название многоступенчатых передач или редукторов. Многоступенчатые передачи, у которых оси вращения колёс неподвижны, носят также рядового соединения.
Рассмотрим рядовое соединение, состоящее из пяти колёс. Входное зубчатое колесо 1 через промежуточные колёса передаёт вращательный момент (мощность) выходному колесу 5. Определим передаточное отношение для каждой пары колёс. Имеем
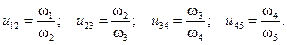 (8)
(8)
Перемножив полученные передаточные отношения (8), получим
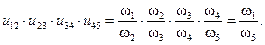
Так как w1/w5 = u15, то
u15 = u12×u23×u34×u45.
Таким образом, передаточное отношение сложной многоступенчатой зубчатой передачи есть произведение взятых со своими знаками передаточных отношений отдельных его ступеней.
Геометрия эвольвентного зацепления
Использование эвольвенты для образования профиля зуба было предложено Леонардом Эйлером (Leonhard Euler) показавшим, что эта кривая обладает рядом преимуществ по сравнению с другими (1767 г.). Из курса математики известно, что эвольвентой, или развёрткой окружности, называют кривую, которую описывает любая точка прямой, касательной к окружности, если эту прямую катить по окружности без скольжения. Окружность радиуса rO, по которой катится прямая, в теории зацепления называют основной окружностью (рис. 5). Пусть задана прямая t – t, касательная к окружности в точке MO. При качении прямой t – t по окружности точка прямой Mt описывает эвольвенту MOE. Для точки M эвольвенты имеем
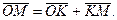
Модуль вектора 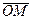 равен
равен
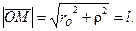 (9)
(9)
Модуль вектора 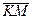 представляет собой радиус кривизны r эвольвенты в точке M. Из уравнения (9) получаем величину
представляет собой радиус кривизны r эвольвенты в точке M. Из уравнения (9) получаем величину
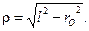 (10)
(10)
Из рис. 5 следует, что
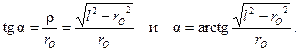 (11)
(11)
Из свойств эвольвенты следует, что отрезок KM равняется дуге KMO, т.е. r = È KMO. В свою очередь дуга È KMO = rO(q + a), откуда
r = rO×(q + a).
Подставляя только что полученное нами выражение для r в равенство (11), получаем
q + a = tg a (12)
или, принимая во внимание формулы (11), имеем
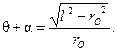
Принимая во внимание равенство (12), найдём угол q, определяющий направление радиуса-вектора  любой точки M эвольвенты:
любой точки M эвольвенты:
q = tg a - a. (13)
К выводу уравнения эвольвенты
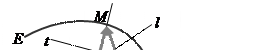
Рисунок 5
Полученная функция угла a называется эвольвентной функцией и обозначается сокращённо inv (involuta). Имеем
q = inv a. (14)
Полученной функцией пользуются для аналитического определения направления радиуса-вектора 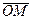 . Так как профили образованы по одному и тому же закону: качением прямой по различным основным окружностям, то они могут быть изготовлены (нарезаны) одним и тем же инструментом. Это является основной причиной широкого использования эвольвентных профилей в современной технике.
. Так как профили образованы по одному и тому же закону: качением прямой по различным основным окружностям, то они могут быть изготовлены (нарезаны) одним и тем же инструментом. Это является основной причиной широкого использования эвольвентных профилей в современной технике.
Планетарные и дифференциальные механизмы
В некоторых многоступенчатых зубчатых передачах оси отдельных колёс являются подвижными. Такие зубчатые механизмы с одной степенью свободы называются планетарными, а с двумя и более степенями свободы – дифференциальными механизмами или просто дифференциалами. В этих механизмах колёса с подвижными осями вращения называются планетарными колёсами или сателлитами, а звено, на котором располагаются оси сателлитов, – водилом. На схемах водило принято обозначать буквой H. Зубчатые колёса с неподвижными осями вращения называются солнечными или центральными; неподвижное колесо – опорным. На рис. 6 показан простейший трёхзвенный планетарный механизм, в котором колесо 1 является опорным, колесо 2 – сателлитом, а звено H – водилом. Звено H входит во вращательные пары O1 со стойкой и O2 с зубчатым колесом 2. При вращении звена H с угловой скоростью wН колесо 2 обегает неподвижное колесо 1, вращаясь с угловой скоростью wН вокруг мгновенного центра вращения P.
Схема трёхзвенного планетарного механизма

Рисунок 6
Связь между угловыми скоростями w2 и wН может быть установлена следующим образом. Для скорости uO2 точки O2, являющейся общей для колеса 2 и водила H, имеем с учётом знаков угловых скоростей w2 и wН:
uO2 = w2×r2 = - wH×(r1 - r2). (15)
Следовательно, передаточное отношение u2H равно
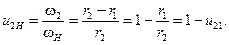 (16)
(16)
Наиболее широкое распространение планетарные зубчатые механизмы получили в планетарных редукторах, предназначенных для получения необходимых передаточных отношений между входным и выходным валами редуктора. Простейшим таким редуктором является планетарный механизм Джемса, состоящий из четырёх звеньев.
Рассмотрим дифференциальный механизм с цилиндрическими колёсами с двумя степенями свободы. Примером такого дифференциала может служить механизм, показанный на рис. 7, у которого сосны колёса 1, 2 и водило H. Колёса 1, 2 и водило H
Схема зубчатого дифференциального механизма с цилиндрическими колёсами

Рисунок 7
вращаются с угловыми скоростями w1, w2 и wН. Число степеней свободы W этого механизма равно двум. В этом механизме число подвижных звеньев n = 4, число вращательных пар V класса p5 = 4. то три пары O1, O2 и OH, в которые входят звенья 1, 2 и H со стойкой, и пара O3, в которую входит водило H и звено 3. Число пар IV класса p4 = 2. Это входящие в зацепление колёса 1, 3 и 3, 2. Следовательно, по структурной формуле число W степеней свободы механизма
W = 3 n – 2 p5 – p4 = 3×4 – 2×4 – 2 = 2.
Таким образом, для определённости движения механизма он должен иметь заданными законы движения двух каких-нибудь звеньев, т.е. иметь две обобщённые координаты. Пусть заданы законы движения звеньев 2 и H, т.е. законами изменения углов поворота j2 и jН звеньев 2 и H. Тогда угол поворота j1 звена 1
j1 = f (j2,jН). (17)
По правилу дифференцирования сложных функций получаем из (17)
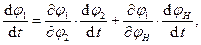 (18)
(18)
или
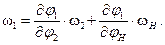 (19)
(19)
Уравнение (19) теперь можно переписать так:
w1 = u12(H)×w2 + u1H(2)×wH. (20)
Из формулы (16) передаточное отношение может быть представлено в следующем виде:
u1H(2) = 1 – u12(H). (21)
Подставляя выражение для из уравнения (21) в уравнение (20), имеем
w1 = u12(H)×w2 + (1 – u12(H)) ×wH,
откуда получаем
w1 = wH + u12(H)×(w2 – wH),
или
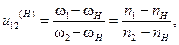 (22)
(22)
где n1, n2 и nH – частоты вращения звеньев 1, 2 и H. Угловая скорость w3 колеса 3 не входит в уравнение, так как колесо 3 является паразитным.
Формула (22) носит название формулы Виллиса для дифференциалов. Формулу Виллиса можно обобщить на дифференциал с любым числом колёс до k. Имеем
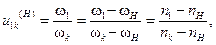 (23)
(23)
Механизмы дифференциалов широко применяются в автомобилях, счётных машинах, сельскохозяйственных машинах т.д.
Дата добавления: 2015-09-21; просмотров: 1259;
