Лекция 15

Тема:Синтез плоских механизмов с низшими парами. Условия существования кривошипа в четырёхзвенных механизмах

Плоские механизмы с низшими парами применяются во многих машинах, приборах и устройствах. Достоинства этих механизмов определяются в основном особыми свойствами низших пар, в которые входят звенья. В низших парах удельное давление и износ меньше чем в высших кинематических парах. Элементы звеньев , образующих эти пары, изготовляются достаточно просто и точно, так как технология обработки плоскостей и цилиндрических поверхностей хорошо развита. Для низших пар на требуется пружин и других устройств, обеспечивающих постоянное замыкание пар.

При помощи плоских механизмов с низшими парами можно теоретически точно воспроизвести любую плоскую алгебраическую кривую. Однако практическое применение этих механизмов ограничивается их многозвенностью. С увеличением же числа звеньев в механизме возрастает вероятность получения недопустимых углов передачи и искажения заданной зависимости вследствие накопления ошибок, происходящих от неточности изготовления механизма. Однако современные методы проектирования механизмов с помощью компьютеров расширяют область их применения.

Целью проектирования (синтеза) кинематической схемы механизма является определение размеров звеньев, при которых будет обеспечено необходимое преобразование движения. Обычно приходится решать задачу синтеза механизма, ведомое (рабочее) звено которого должно иметь возвратно-вращательное или возвратно-поступательное движение.

Как правило, бывает задано полное перемещение ведомого звена S или y и относительное положение осей вращения или направляющих ведущего и ведомого звеньев. В отдельных случаях могут быть наложены ограничения на углы давления.

Синтез шарнирного четырёхзвенника по заданному ходу коромысла. Пусть заданы крайние положения B₁C и B₂C коромысла (ведомого звена) и, следовательно, угол y его поворота (рис. 1); кривошип OA должен делать полный оборот. Точка O может быть выбрана произвольно. Соединяем её с точками B₁ и B₂. Из чертежа следует:

OB₁ = l – r и OB₂ = l + r, (1)

где r – радиус кривошипа OA; l – длина шатуна AB.

Проектирование шарнирного четырёхзвенника по заданному ходу коромысла

Рисунок 1

Из рис. 1 следует, что

OB₂ – OB₁ = l + r – l + r = 2 r, (2)

откуда

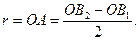(3)

Синтез шарнирного четырёхзвенника по заданному коэффициенту увеличения средней скорости коромысла. Из рис. 1 видно, что коэффициент увеличения средней скорости равен

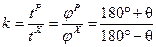(4)

и зависит от угла q между направлениями кривошипа в крайних положениях механизма. Тогда угол q

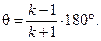(5)

Синтез кривошипно-ползунного механизма по заданному перемещению S ползуна. Это перемещение можно выполнить при различных размерах шатуна. Поэтому обычно дополнительно задают максимальное расстояние x_max от крайнего положения ползуна до шарнира A кривошипа. Этот размер определяет габариты проектируемого механизма. Для аксиального механизма (на рис. 2) имеем

OB₂ = x_max = l + r; B₁B₂ = S = 2 r,

откуда

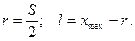
Проектирование кривошипно-ползунного механизма

Рисунок 2

Если заданы дополнительные условия, то построенный центральный (аксиальный) механизм может не удовлетворять этим условиям. Тогда необходимо переходить к дезаксиальному механизму и определять параметры l, r и a этого механизма.

Дополнительно могут быть заданы:

a) наибольший допустимый угол давления g_max внутри рабочего хода. Из рис. 2 следует, что можно составить следующие три уравнения:

a² + (x_max - S)² = (l - r)²,

a² + x_max² = (l + r)²,

r - a = l sin g_max.

Решая их совместно, определяем основные размеры дезаксиального кривошипно-ползунного механизма:

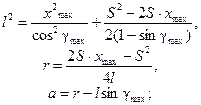
b) величина отношения 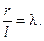Тогда для определения l, r и a используем уравнения

a² + (x_max - S)² = (l - r)², a² + x_max² = (l + r)², r = l×l,

решая которые получаем

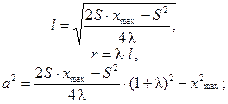
c) при заданных S, g_max и l можно спроектировать дезаксиальный механизм. Для определения параметров l, r и a (a - эксцентриситет) механизма используем следующие три уравнения (см. рис. 2):

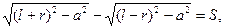r - l×sin g_max = a, r = l×l.

Решая их совместно, находим

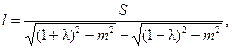
где

m = l - sin g_max.

По найденной величине l из второго и третьего уравнений находят r и a.

Условия существования кривошипа в четырёхзвенных механизмах

Пусть дан механизм шарнирного четырёхзвенника ABCD (рис. 3), у которого длины звеньев обозначены через a, b, c и d. Требуется выяснить, при каких условиях звено AB будет кривошипом, т.е. будет проворачиваться на угол 2p, если принято, что a<b<c<d. Соединим точки B и D прямой и обозначим расстояние BD через f. Тогда из треугольника ABD следует:

f ² = a ² + d ² - 2a×d×cos j, (6)

а из треугольника BCD имеем:

b + c ³ f ³ c - b. (7)

Из выражения (6) получаем

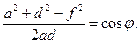
Принимая во внимание неравенства (7), имеем

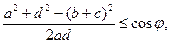(8)

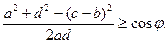(9)

Если звено a поворачивается на угол 2p, то угол j принимает значения от 0 до 2p и cos j меняется в пределах от +1 до -1. Так как левая часть неравенства (8) должна быть меньше наименьшего значения cos j, а левая часть неравенства (9) должна быть больше наибольшего значения cos j, то

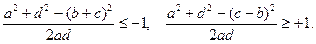
Из этих неравенств имеем

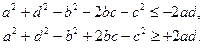
Отсюда перенесением членов имеем

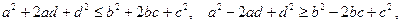
или

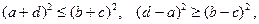
и окончательно

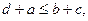(10)

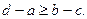(11)

Неравенство (11) может быть представлено так:

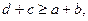
но последнее неравенство вытекает из принятого ранее условия a < b < c < d, т.е. неравенство (11) не даёт никаких новых условий.

Из неравенства (10) следует: чтобы в шарнирном четырёхзвеннике, у которого стороны удовлетворяют условию a < b < c < d, звено a было кривошипом, необходимо, чтобы сумма длин наименьшего и наибольшего звеньев была меньше или равна сумме длин двух других звеньев.

К условию существования кривошипа К условию существования кривошипа

у шарнирного четырёхзвенника у кривошипно-ползунного механизма

Рисунок 3 Рисунок 4

С помощью условий (10) и (11) можно показать, что если в механизме, у которого a<b<c<d (рис. 3), сделать неподвижным звено b и d, то получим кривошипно-коромысловый механизм. Если неподвижным сделать наименьшее звено a, то механизм будет двухкривошипным, и, наконец, если неподвижным сделать звено c, то механизм превращается в двухкоромысловый.

Все шарнирные четырёхзвенники распределяются по двум группам. К первой относятся те, у которых сумма длин наименьшего и наибольшего звеньев меньше или равна сумме длин двух других звеньев; ко второй – в которых эта сумма больше суммы остальных. Механизмы первой группы при постановке на наименьшее звено представляют собой двухкривошипные механизмы, при постановке на звено, смежное с ним, – кривошипно-коромысловые, причём кривошипом служит наименьшее звено, а при постановке на звено, противоположное наименьшему, – двухкоромысловые. Механизмы второй группы все двухкоромысловые.

Если, подобно шарнирному четырёхзвеннику, написать соотношения между размерами звеньев кривошипно-ползунного механизма (рис. 4), то получим, что звено a будет кривошипом, если

a < b – e,

где e есть дезаксиаль (эксцентриситет). Звено a будет коромыслом, если

a > b – e.