Лекция 10. Тема: Силовой расчёт. Силы инерции звеньев

Тема: Силовой расчёт. Силы инерции звеньев. Статическая определимость кинематических цепей.

План лекции.

Задачи и методы

Для расчёта элементов кинематических пар и звеньев на прочность и определения их конструктивных размеров предварительно определяют действующие на них при движении механизма силы.

Как правило, заданными являются силы полезных сопротивлений, приложенные к ведомому звену. Некоторые звенья механизмов имеют неравномерное движение и испытывают переменные по величине и направлению ускорения. Поэтому реакции (давления) в кинематических парах зависят не только от внешних приложенных к механизму сил, например от сил полезных сопротивлений, но и от дополнительных динамических давлений, возникающих из-за неравномерного движения звеньев. Величина и направление динамических давлений зависят от сил инерции звеньев.

Известно, что если силы инерции твёрдых тел (звеньев) условно приложить к последним, то эти силы уравновесятся с внешними, приложенными к звеньям механизма силами.

Следовательно, если к механизму, кроме сил внешних, приложить ещё и силы инерции его звеньев, то условно можно считать, что механизм находится в покое (равновесии). В этом случае для определения давлений в кинематических парах можно использовать уравнения статики, если в них включить силы инерции звена. Решая эти уравнения, определим давления в кинематических парах движущегося механизма.

Так как в уравнения статики вошли силы инерции звеньев, возникающие при движении механизма, то такой метод расчёта называют кинетостатическим.

Для упрощения расчёта трением между элементами кинематических пар пренебрегают. Сначала определяют давления в кинематических парах. Затем, выбрав значения коэффициентов трения, можно подсчитать силы трения, возникающие в кинематических парах механизмов. В результате кинетостатического расчёта можно определить усилие, которое оказывают на ведущее звено силы полезных сопротивлений, приложенные к механизму, и силы инерции его звеньев. Момент, равный моменту этой силы относительно оси вращения кривошипа и направленный в обратную сторону, равен тому движущему моменту М_Д, который должен быть приложен со стороны двигателя к ведущему звену, чтобы механизм, нагруженный заданными силами полезных сопротивлений, двигался по заданному закону.

Силы инерции звеньев

Силы инерции материальных точек звена могут быть приведены к одной точке и, таким образом, представлены их главным вектором и главным моментом.

Главный вектор сил инерции, называемый обычно силой инерции звена, равен

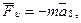(1)

где m [кг] – масса звена, 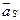[м×с ^{– 2}] – ускорение центра S масс звена. Направление силы инерции 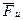противоположно направлению вектора 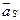. Её размерность [кг×м×с ^{– 2}], т.е. она измеряется в ньютонах [H].

Рассмотрим звено, которое совершает плоскопараллельное движение и имеет плоскость материальной симметрии, параллельную плоскости его движения. Точкой приведения сил инерции звена следует брать его центр масс (рис. 1). Тогда упрощается выражение момента инерционной пары сил – главного момента сил инерции, что то же, инерционного момента. Он равен

M_u = - I_S ×e, (2)

где I_S [кг×м ²] – момент инерции масс звена относительно оси, проходящей через его центр масс перпендикулярно плоскости его материальной симметрии, или, иначе, центральный момент инерции звена, e [c ^{– 2}] – угловое ускорение звена.

Инерционная нагрузка звена

Рисунок 1

Инерционный момент M_u имеет размерность [кг×м×с ^{– 2}] = [Н×м]. Плоскость, в которой он действует, параллельна плоскости движения звена; он направлен в сторону, противоположную направлению углового ускорения звена.

Таким образом, в общем случае инерционная нагрузка звена представляется одной инерционной силой 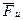, приложенной в точке S и определяемой формулой (1), и одним инерционным моментом M_u , определяемым формулой (2).

Частные случаи (рис. 2).

Поступательное движение звена (рис. 2, a). Инерционная нагрузка состоит только из одной инерционной силы 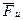, определяемой формулой (1).

Неравномерное вращательное движение звена (рис. 2, b). Инерционная нагрузка состоит из силы инерции 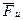, определяемой формулой (1), и инерционного момента M_u , определяемого формулой (2). Модуль полного ускорения центра масс звена в этом случае равен

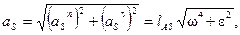(3)

где a_Sⁿ и a_S^t – нормальное и тангенциальное ускорения центра масс звена, w и e – угловая скорость и угловое ускорение звена, l_AS – расстояние от центра масс S до оси A вращения звена.

Силу 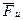и момент M_u можно привести к одной силе 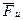. Для этого следует силу 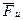приложить, сохраняя её направление, в центре K качания звена (рис. 2, c). Расстояние l_AK центра качания K от оси вращения последнего A равно

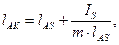(4)

I_S – центральный момент инерции звена, m – его масса.

Равномерное вращательное движение звена (рис. 2, d). Инерционная нагрузка состоит только из силы инерции 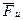звена, которая в этом случае направлена по линии AS

Частные случаи инерционной нагрузки звена

a)

b)

c) d)

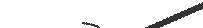e) f)

Рисунок 2

противоположно направлению вектора нормального ускорения центра масс звена. Это ускорение равно

a_Sⁿ = w²×l_AS , (5)

и, следовательно, центробежная сила инерции будет равна

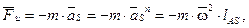(6)

Произведение m×l_AS называется неуравновешенностью или дисбалансом и имеет размерность [кг×м].

Неравномерное вращательное движение звена при совпадении центра масс S звена с его осью вращения A (рис. 2, e). Инерционная нагрузка звена состоит только из инерционного момента M_u , который находится по формуле (2).

Равномерное вращательное движение звена при совпадении центра масс S звена с его осью вращения A (рис. 2, f). В этом случае l_AS = 0 и в соответствии с формулой (3) a_S = 0, следовательно, 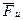= 0, и так как e = 0 (равномерное вращение), то M_u = 0. Инерционная нагрузка звена равна нулю и оно называется уравновешенным.

Чтобы найти инерционную нагрузку всех звеньев какого-нибудь механизма для заданного положения, необходимо построить планы скоростей и ускорений. Подсчитывается инерционная нагрузка для каждого звена механизма: инерционная сила и инерционный момент.

Статическая определимость структурных групп

Равнодействующая F давлений между элементами низшей кинематической пары определяется величиной, направлением и точкой приложения. Если не учитывать трение, то во вращательной паре всегда известна точка приложения силы F (центр шипа), а в поступательной – её направление (перпендикуляр к направляющей) (рис. 3).

Давления в кинематических парах

a b

a) вращательная пара, b) поступательная пара

Рисунок 3

Следовательно, в каждой низшей паре неизвестны два параметра силы F. Для каждого из подвижных звеньев плоского механизма можно написать три уравнения равновесия, а для всех подвижных звеньев – 3 n уравнений. Для определения давления в каждой из низших пар, как было указано, достаточно определить два неизвестных.

Кинематическая цепь является статически определимой, если она удовлетворяет условию 3 n = 2 p₅ (число уравнений статики равно числу неизвестных параметров приложенных к ней сил). Ранее было показано, что условию 3 n = 2 p₅ удовлетворяют структурные группы. Следовательно, структурная группа звеньев статически определима. Поэтому методы кинетостатического расчёта разработаны применительно к различным типам структурных групп. Как было показано в лекции 7, при кинематическом исследовании механизма порядок исследования совпадает с порядком присоединения групп, т.е. вначале рассматривается группа, присоединяемая к начальному или начальным звеньям и стойке. Потом рассматривается следующая группа и т.д. Порядок силового расчёта является обратным порядку кинематического исследования, т.е. силовой расчёт начинается с последней (считая от начального звена) присоединённой группы и кончается силовым расчётом начального звена.

Пусть, например, подлежит силовому расчёту шестизвенный механизм, показанный на рис. 4. К начальному звену 1 и стойке 6 присоединена первая группа II класса, состоящая из звеньев 2 и 3. Далее к звену 2 и стойке 6 присоединена вторая группа II класса, состоящая из звеньев 4 и 5. Силовой расчёт следует начинать с последней по присоединению группы, т.е. с группы, состоящей из звеньев 4 и 5, после этого следует перейти к группе, состоящей из звеньев 2 и 3 и, наконец, к силовому расчёту начального звена 1.

К порядку силового расчёта шестизвенного механизма

Рисунок 4