Лекция 11. Тема: Силовой расчёт механизмов
Тема: Силовой расчёт механизмов. Определение реакций в кинематических парах.
План лекции.
Силовой расчёт шарнирного четырёхзвенника
Схема механизма и данные о нём приведены в лекции 8. Данные о массах звеньев следующие: m1 = 0.7 кг, m2 = 1.15 кг, m3 = 0.8 кг. Ускорения центров масс звеньев определены ранее. Ускорение свободного падения принимаем равным g » 9.8 м×с – 2.
Определяется инерционная нагрузка звеньев механизма. Силы инерции определяем используя построенный план ускорений. Сила инерции рассматриваемого звена равна
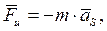
где m – масса этого звена (кг); aS – ускорение центра масс звена (м×с – 2). Направление силы инерции 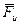 противоположно направлению вектора
противоположно направлению вектора 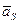 . Её размерность (кг×м×с – 2), т.е. она измеряется в ньютонах (Н). Считаем, что звено совершает плоскопараллельное движение. При этом точкой приведения сил инерции берём его центр масс, так как упрощается выражение момента инерционной пары сил или инерционного момента. Он равен
. Её размерность (кг×м×с – 2), т.е. она измеряется в ньютонах (Н). Считаем, что звено совершает плоскопараллельное движение. При этом точкой приведения сил инерции берём его центр масс, так как упрощается выражение момента инерционной пары сил или инерционного момента. Он равен
Mu = - IS×e,
где IS (кг×м 2) – момент инерции масс звена относительно оси, проходящей через его центр масс перпендикулярно плоскости его материальной симметрии, или, иначе, центральный момент инерции звена; e (с – 2) – угловое ускорение звена.
Инерционный момент звена Mu имеет размерность (кг×м 2×с–2) = (Н×м). Плоскость, в которой он действует, параллельна плоскости движения звена; он направлен в сторону, противоположную направлению углового ускорения звена.
Сила инерции кривошипа по модулю
Fu1 = m1×aS1 = 0.7×7.9 » 5.5 H
приложена в центре масс кривошипа S1 и по направлению противоположна вектору ускорения aS1 этого звена.
Сила инерции звена 2 (шатуна)
Fu2 = m2×aS2 = 1.15×44 = 50.6 H
приложена в центре масс шатуна S2 и по направлению противоположна вектору ускорения aS2 этого звена.
Сила инерции звена 3 (коромысла)
Fu3 = m3×aS3 = 0.8×26 = 20.8 H
приложена в центре масс коромысла S3 и по направлению противоположна вектору ускорения aS3 этого звена.
Инерционный момент звена 1 (кривошипа OA) равен нулю Mu1 = 0, так как оно вращается равномерно.
Для звена 2 (шатуна) инерционный момент Mu2 найдём по формуле
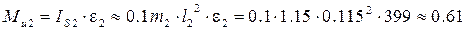 Н×м.
Н×м.
Для звена 3 (коромысла) инерционный момент Mu3 найдём по формуле
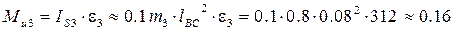 Н×м.
Н×м.
Силовой расчёт группы звеньев 2 и 3
Расчёт начинаем с присоединённой группы Ассура, затем переходим к расчёту ведущего звена. Группа Ассура является статически определимой системой, поэтому используем известные из теоретической механики уравнения равновесия всей группы или отдельных её звеньев в форме
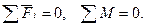
В число сил и моментов, входящих в эти уравнения, включаются реакции и моменты реакций в кинематических парах группы.
На основании уравнений строится многоугольник сил, который носит название плана сил, причём в первую очередь находятся реакции во внешних кинематических парах группы, а затем во внутренних парах по условиям равновесия звеньев группы, взятых порознь.
Составляем уравнение равновесия группы, состоящей из звеньев 2 и 3
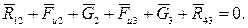
В этом уравнении содержится четыре неизвестных: величина и направление реакции 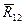 и величина и направление реакции
и величина и направление реакции 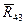 . Для того чтобы его решить, т.е. чтобы построить представленную им векторную сумму, разложим каждую из этих реакций
. Для того чтобы его решить, т.е. чтобы построить представленную им векторную сумму, разложим каждую из этих реакций 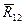 и
и 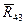 на две составляющие: одну, действующую по оси звена, и другую, перпендикулярную к оси звена (рис. 5). Будем обозначать первую составляющую реакции индексом n, а вторую составляющую – индексом t. Теперь геометрическая сумма сил, приложенных к группе, равна
на две составляющие: одну, действующую по оси звена, и другую, перпендикулярную к оси звена (рис. 5). Будем обозначать первую составляющую реакции индексом n, а вторую составляющую – индексом t. Теперь геометрическая сумма сил, приложенных к группе, равна
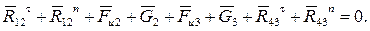
Инерционная нагрузка группы звеньев 2 и 3

Рисунок 5
Величину силы 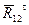 найдём, рассматривая равновесие звена 2. Напишем равенство нулю суммы моментов относительно точки B всех сил, приложенных к звену 2 (тем самым исключим из него момент неизвестной реакции
найдём, рассматривая равновесие звена 2. Напишем равенство нулю суммы моментов относительно точки B всех сил, приложенных к звену 2 (тем самым исключим из него момент неизвестной реакции 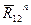 ).
).
Уравнение равновесия для второго звена
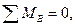
которое будучи развёрнутым, примет вид
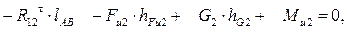
откуда
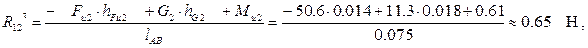
где плечи известных сил найдены по чертежу и выражены в метрах.
Величину силы 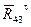 найдём, рассматривая равновесие звена 3. Напишем равенство нулю суммы моментов относительно тоски B всех сил, приложенных к звену 3 (тем самым исключим из него момент неизвестной реакции
найдём, рассматривая равновесие звена 3. Напишем равенство нулю суммы моментов относительно тоски B всех сил, приложенных к звену 3 (тем самым исключим из него момент неизвестной реакции 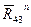 ).
).
Уравнение равновесия для третьего звена
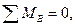
которое будучи развёрнутым, примет вид
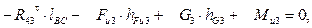
откуда
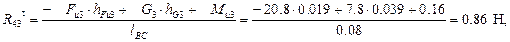
где плечи известных сил найдены по чертежу и выражены в метрах.
Строим план сил группы по уравнению её равновесия в масштабе 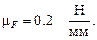
Порядок построения векторной суммы, вообще говоря, безразличен, но применительно к группам Ассура можно рекомендовать следующий: назначаем обход контура группы в каком-либо направлении (например, по ходу часовой стрелки) и силы откладываем в такой последовательности, в какой мы эти силы встречаем на группе при обходе её контура в выбранном направлении (рис. 6). Примем обход контура по ходу часовой стрелки.
Отложим от точки a силу 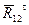 в виде отрезка
в виде отрезка 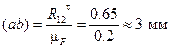 ,
,
от точки b отложим силу 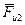 в виде отрезка
в виде отрезка 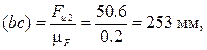
от точки c отложим силу 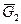 в виде отрезка
в виде отрезка 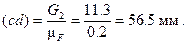
От точки d отложим силу 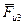 в виде отрезка
в виде отрезка 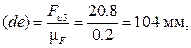
от точки e отложим силу 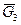 в виде отрезка
в виде отрезка 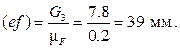
От точки f отложим силу 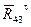 в виде отрезка
в виде отрезка 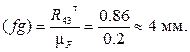
План сил группы звеньев 2 и 3

Рисунок 6
Через точку a проводим прямую, параллельную линии AB. Это будет линия действия силы 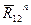 , а через точку g – прямую, параллельную BC. Она будет линией действия силы
, а через точку g – прямую, параллельную BC. Она будет линией действия силы 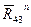 . Находим точку пересечения k этих прямых.
. Находим точку пересечения k этих прямых.
Отрезок (ka) в масштабе mF даёт искомую реакцию 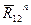 , а отрезок (gk) в том же масштабе – реакцию
, а отрезок (gk) в том же масштабе – реакцию 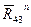 и, наконец, отрезок (kb) даёт искомую реакцию
и, наконец, отрезок (kb) даёт искомую реакцию 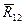 , а отрезок (fk) – реакцию
, а отрезок (fk) – реакцию 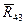 .
.
Реакция R12n = (ka)×mF = 178×0.2=35.6 H.
Полная реакция R12 = (kb)×mF = 178×0.2=35.6 H.
Реакция R43n = (gk)×mF = 478×0.2=95.6 H.
Полная реакция R43 = (fk)×mF = 479×0.2=95.8 H.
Для нахождения реакции 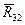 напишем условие равновесия звена 2:
напишем условие равновесия звена 2:
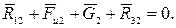
Из плана сил видно, что отрезок (dk) в масштабе mF соответствует искомой реакции 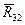 .
.
Реакция R32 = (dk)×mF = 382×0.2=76.4 H.
Силовой расчёт ведущего звена
К звену 1 приложены: сила 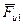 , сила
, сила 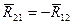 (её величина определена из плана сил отрезком (kb)), вес
(её величина определена из плана сил отрезком (kb)), вес 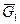 , сила
, сила 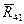 и уравновешивающий момент My (рис. 7).
и уравновешивающий момент My (рис. 7).
Из равенства нулю суммы моментов относительно точки O сил, приложенных к кривошипу (звену 1), находим величину момента уравновешивающей пары сил:
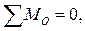
- My + R21×h21 - G1×hG1 = 0, - Fy×lOA + R21×h21 - G1×hG1 = 0.
Отсюда находим уравновешивающую силу 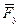 , считая её приложенной в точке A и действующей перпендикулярно к кривошипу:
, считая её приложенной в точке A и действующей перпендикулярно к кривошипу:
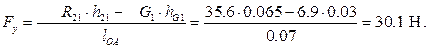
Для определения реакции 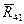 неподвижного звена 4 на звено 1 составим уравнение равновесия сил, приложенных к звену 1:
неподвижного звена 4 на звено 1 составим уравнение равновесия сил, приложенных к звену 1:
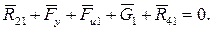
Силовая нагрузка ведущего звена

Рисунок 7
Строим план сил (рис. 8) по уравнению равновесия в масштабе сил 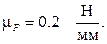 Отложим реакцию
Отложим реакцию 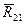 от произвольно взятой точки a в виде отрезка (ab)
от произвольно взятой точки a в виде отрезка (ab)
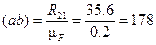 мм,
мм,
уравновешивающую силу 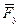 - в виде отрезка (bc)
- в виде отрезка (bc)
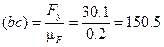 мм,
мм,
силу инерции 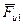 - в виде отрезка (cd)
- в виде отрезка (cd)
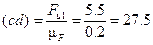 мм,
мм,
вес кривошипа 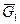 - в виде отрезка (de)
- в виде отрезка (de)
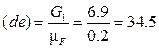 мм.
мм.
Отсюда находим модуль реакции 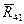 по длине отрезка (ea)
по длине отрезка (ea)
R41 = (ea)×mF = 58×0.2=11.6 H.
На этом завершается кинетостатическое исследование механизма.
План сил ведущего звена (план повёрнут на 60° против хода часовой стрелки)

Рисунок 8
Дата добавления: 2015-09-21; просмотров: 1080;
