Лекция 8. Тема: Построение планов скоростей и ускорений механизма, образованного группой Ассура 2–го класса 1–го вида.

Тема: Построение планов скоростей и ускорений механизма, образованного группой Ассура 2–го класса 1–го вида.

Построение плана скоростей

Планы скоростей и ускорений механизма строятся после решения задачи о его положении, причём построение планов проводится для отдельных групп Ассура, которые образовали механизм. Вначале строится план скоростей (ускорений) группы, которая присоединена элементами своих внешних кинематических пар к ведущему звену и стойке, затем строятся планы скоростей (ускорений) второй и т.д. групп, взятых в той же последовательности, в какой они присоединяются при образовании механизма.

Рассмотрим двухкривошипный шарнирный четырёхзвенник. Данные: l_OA = 0.07 м, l_OC = 0.04 м, l_BC = 0.08 м, l_AB = 0.075 м, l_BD = 0.04, j₁ = 30°, угловая скорость кривошипа OA постоянна и равна w₁ = 15 c ^{– 1} (рис. 1).

План положения механизма

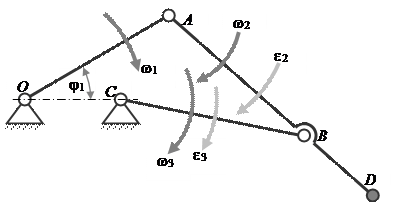
Рисунок 1

Сначала строим план заданного положения механизма. Масштаб длин принимаем равным m_l = 0.001 м /мм. Вычисляем длины отрезков, изображающие на чертеже звенья.

Для каждого положения механизма определяются скорости точек графическим методом. Вначале определяем скорость точки A, принадлежащей ведущему звену, которое вращается равномерно с постоянной угловой скоростью w₁. Скорость этой точки по модулю равна

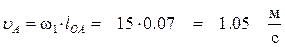
и направлена перпендикулярно оси звена OA в сторону вращения. Отложим от произвольной точки p, называемой полюсом плана скоростей, отрезок (pa). Длину отрезка (pa) выбираем равной (OA). (pa) = (OA) = 70 мм. Вычисляем масштабный коэффициент скоростей:

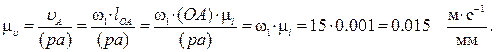
Строим план скоростей для группы звеньев 2 и 3. Оба звена совершают плоскопараллельное движение. Из теоретической механики известно, что скорость любой точки B плоской фигуры геометрически складывается из скорости какой-нибудь точки A, принятой за полюс, и скорости, которую точка B получает при вращении фигуры вокруг этого полюса.В этой группе звеньев все пары вращательные. Определяем скорость точки B по следующим двум векторным уравнениям:

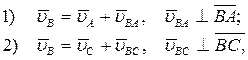
где 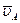- скорость точки A, нам известная; 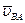- скорость точки B при вращении звена BA вокруг оси шарнира A, по модулю равная u_BA = w₂×l_BA (w₂ – угловая скорость звена BA, которая пока нам неизвестна) и направленная перпендикулярно линии BA; 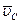– скорость точки C стойки 4 (она равна нулю, так как звено 4 неподвижно); 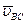– скорость точки B при вращении звена BC вокруг оси шарнира C, по модулю равная u_BС = w₃×l_BС (w₃ - угловая скорость звена BC, которая пока нам неизвестная) и направленная перпендикулярно линии BC.

Построение плана скоростей ведём в такой последовательности. Строим решение первого векторного уравнения, указанного выше: из точки a проводим направление скорости изображающий 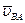- линию, перпендикулярную BA. Строим решение второго векторного уравнения, указанного выше: из точки p надо было отложить скорость 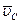, но она равна нулю, поэтому точку c совмещаем с полюсом плана скоростей p; из точки c или, что то же, p проводим направление скорости 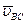- линию, перпендикулярную BC, до пересечения с линией, проведённой перпендикулярно BA, и получаем точку b - конец вектора скорости точки B. Помещаем в полюс плана точку o. Скорость точки D находим по правилу подобия: конец вектора этой скорости должен лежать на продолжении отрезка (ab). Составляем следующую пропорцию:

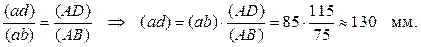
Определяем скорость точки B: u_B = (pb)×m_u = 128×0.015 = 1.92 м/c.

Определяем скорость точки D: u_D = (pd)×m_u = 169×0.015 » 2.54 м/c.

Определяем угловую скорость звена AB:

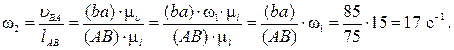
План скоростей механизма

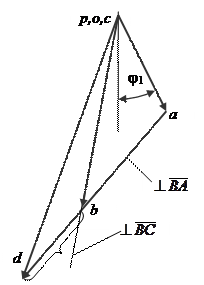Рисунок 2

Направление угловой скорости w₂ звена AB может быть определено следующим образом. Мысленно прикладывая вектор 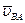к точке B, видим, что вращение звена 2 вокруг оси шарнира A, принятой за полюс, совпадает с направлением вращения часовой стрелки. Отмечаем нужное направление вращения на звене 2 в виде дуговой стрелки.

Определяем угловую скорость звена BC:

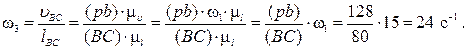
Направление угловой скорости w₃ звена BC определяется таким же образом, как и w₂. Мысленно прикладывая вектор 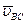к точке B, видим, что вращение звена 3 вокруг оси шарнира C, принятой за полюс, совпадает с направлением вращения часовой стрелки. Отмечаем нужное направление вращения звена 3 дуговой стрелкой.

Построение плана ускорений

Ускорения точек находятся методом плана ускорений. Вначале определяем скорость точки A, принадлежащей ведущему звену, которое вращается равномерно с постоянной угловой скоростью w₁. Полное ускорение точки A определяется по формуле 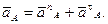Так как e₁ = 0, то тангенциальное ускорение a^t_A = 0. Тогда 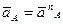и ускорение точки A легко вычисляется: a_A = w₁²×l_OA. Затем строим план ускорений для группы звеньев 2 и 3. Так как движение этих звеньев плоское и все пары вращательные, то используем известную из теоретической механики теорему: ускорение любой точки B плоской фигуры геометрически складывается из ускорения какой-нибудь точки A, принятой за полюс, и ускорения, которое точка B получает при вращении фигуры вокруг этого полюса. Этот план строится по таким двум векторным уравнениям:

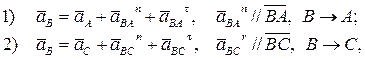
где 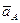- полное ускорение точки A, равное нормальному ускорению 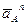, так как звено 1 (кривошип) вращается равномерно и угловое ускорение равно нулю, следовательно равно нулю и тангенциальное ускорение ,

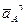a_A = a_Aⁿ = w₁²×l_OA

и направленное параллельно линии OA от точки A к точке O (к центру кривизны траектории);

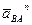- нормальное ускорение точки B во вращательном движении звена AB вокруг точки A, по модулю равное

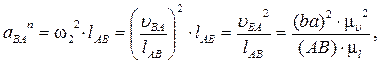
и направленное параллельно линии AB от точки B к точке A ( );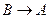

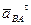- тангенциальное ускорение точки B в том же движении звена AB, по модулю равное

a_BA^t = e₂×l_AB

(e₂ - угловое ускорение звена AB, пока нам неизвестное) и направленное перпендикулярно линии AB;

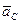- ускорение точки C, равное нулю, так как звено 4 неподвижно;

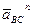- нормальное ускорение точки B во вращательном движении звена BC вокруг точки C, по модулю равное

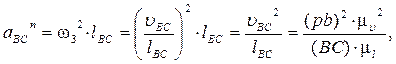
и направленное параллельно линии BC от точки B к точке C ( );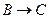

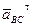- тангенциальное ускорение точки B в том же движении звена BC, по модулю равное

a_BC^t = e₃×l_BC

(e₃ - угловое ускорение звена BC, пока нам неизвестное) и направленное перпендикулярно линии BC.

Построение плана ускорений ведём в следующей последовательности. Строим решение первого векторного уравнения, указанного выше, для чего от полюса плана p откладываем отрезок (pa), изображающий ускорение 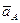, параллельно линии OA. Длину отрезка (pa) принимаем равной 70 мм, отчего масштаб ускорений будет

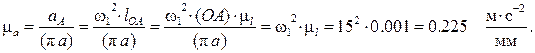
От точки a откладываем отрезок (an_BA), изображающий ускорение 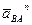. Длина отрезка (an_BA) вычисляется так:

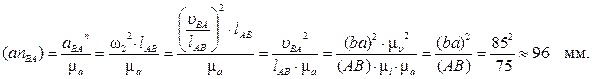
Через точку n_BA проводим направление ускорения 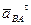- линию, перпендикулярную линии AB. Переходим к построению решения второго векторного уравнения, указанного выше. Для этого от полюса плана p откладываем вектор ускорения 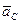, но оно равно нулю, поэтому точка c совпадает с точкой p. От точки p откладываем отрезок (pn_BC), изображающий ускорение 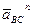. Длина отрезка (pn_BC) вычисляется так:

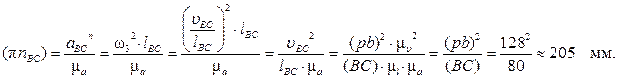
Через точку n_BC проводим направление ускорения 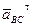- линию, перпендикулярную линии BC. Точка пересечения её с линией, проведённой перпендикулярно AB, даёт точку b - конец вектора ускорения точки B. Соединяем точки b и a и получаем вектор полного ускорения точки B при вращении звена AB относительно точки A, т.е. 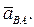Точку o совмещаем с точкой p (полюсом плана). На этом заканчиваем построение плана ускорений механизма. Конец вектора ускорения точки D найдём по правилу подобия:

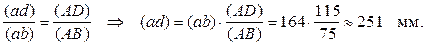
Соединив точку d с полюсом плана p, получаем отрезок (pd), изображающий абсолютное ускорение точки D.

Величины абсолютных ускорений точек B и D определяются так:

a_B = (pb)×m_a = 232×0.225 » 52 м×c ^{– 2};

a_D = (pd)× m_a = 320×0.225 = 72 м×c ^{– 2}.

По правилу подобия найдём ускорения центров масс подвижных звеньев. Точки S₁, S₂ и S₃ находятся на серединах соответствующих звеньев. На плане ускорений это будут векторы: (ps₁), (ps₂) и (ps₃). Определяем абсолютные величины ускорений этих центров масс:

a_S1 = (ps₁) ×m_a = 35×0.225 » 7.9 м×c ^{– 2};

a_S2 = (ps₂) ×m_a = 194×0.225 » 44 м×c ^{– 2};

a_S3 = (ps₃)×m_a = 116×0.225 » 26 м×c ^{– 2}.

Величина углового ускорения звена AB равна:

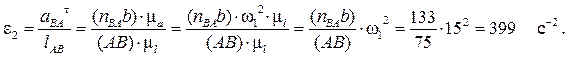
Направление углового ускорения e₂ звена 2 (звена AB) может быть определено следующим образом. Перенося мысленно вектор 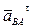в точку B, видим из точки A, что направление e₂ совпадает с направлением вращения часовой стрелки. Обозначаем направление углового ускорения e₂ на плане положения звена 2 дуговой стрелкой.

Величина углового ускорения звена BC равна:

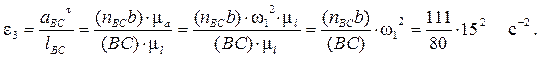
Направление углового ускорения e₃ звена 3 (звена BC) может быть определено таким же образом, как и e₂. Перенося мысленно вектор 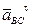в точку B, видим из точки C, что направление e₃ совпадает с направлением вращения часовой стрелки. Обозначаем направление углового ускорения e₃ на плане положения звена 3 дуговой стрелкой. План ускорений механизма приведён на рис. 3.

План ускорений механизма

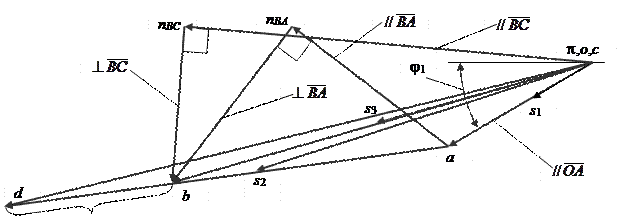Рисунок 3