Лекция 7. Тема: Кинематическое исследование плоских рычажных механизмов графическим методом
Тема: Кинематическое исследование плоских рычажных механизмов графическим методом. Масштабные коэффициенты. Определение положений звеньев групп и построение траекторий точек.
План лекции.
При кинематическом исследовании механизмов рассматриваются следующие основные вопросы:
a) построение планов механизма и траекторий, которые описывают отдельные точки, расположенные на его звеньях;
b) определение скоростей и ускорений точек, расположенных на звеньях механизма, и угловых скоростей и ускорений отдельных звеньев.
Все перечисленные вопросы могут быть решены аналитическим, экспериментальным или графическим методами.
Экспериментальный метод может быть применён только при наличии соответствующей лаборатории. Аналитический метод удобен только при анализе простых механизмов, так как аналитическое решение сложных механизмов сводится к очень большому числу уравнений и оказывается трудно выполнимым. В теории механизмов и машин разработаны графоаналитические методы, позволяющие быстро решать вопросы кинематического исследования с достаточной для практических расчётов точностью. При кинематическом исследовании за исходные данные принимают: 1) размеры звеньев механизма и его кинематическую схему и 2) закон движения начального звена.
Масштабы, применяемые в теории механизмов и машин
При выполнении графических построений на чертеже приходится изображать в масштабе длины звеньев, скорости и ускорения отдельных точек, силы и многие другие величины. Хотя понятие масштаба совершенно элементарно, но, как показала практика расчётов, большинство ошибок при графических построениях связано с масштабом. Поэтому применяя графический и графоаналитический методы исследования механизмов следует весьма тщательно подсчитывать масштабы.
В курсе теории механизмов и машин принято понимать под масштабом той или иной величины отношение этой величины к отрезку, который её изображает на чертеже.
Допустим, что какая-либо физическая величина N изображена на чертеже отрезком, имеющим длину X миллиметров, тогда масштабом m (или масштабным коэффициентом) будет называться отношение:
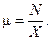
Из этой формулы следует, что масштаб всегда величина именованная, показывающая сколько истинных величин содержится в одном миллиметре чертежа. В теории механизмов и машин, как и в других областях науки и техники, обязательно используется Международная система единиц (СИотSI – System International). Длина выражается в метрах (м), масса – в килограммах (кг), сила и вес – в ньютонах (Н), время – в секундах (с). Причём, в механике единицы длины, массы и времени являются основными, а единица силы и веса – производная единица СИ, имеющая собственное наименование. Ньютон есть сила, сообщающая телу массой 1 кг ускорение 1 м/c2 в направлении силы.
В Международной системе единиц приняты десятичные кратные и дольные единицы от исходных единиц СИ, получаемые путём умножения их на число 10 в соответствующей положительной (для кратных единиц) или отрицательной (для дольных единиц) степени. Наименование десятичных кратных и дольных единиц образуются прибавлением приставок к наименованиям исходных единиц. Некоторые часто встречающиеся десятичные приставки приведены ниже.
| Приставка для кратных единиц | Множитель | Приставка для дольных единиц | Множитель |
| мега (М) | 10 6 | деци (д) | 10 – 1 |
| кило (к) | 10 3 | санти (с) | 10 – 2 |
| гекто (г) | 10 2 | милли (м) | 10 – 3 |
| дека (да) | микро (мк) | 10 – 6 |
Масштабы для планов положений, скоростей и ускорений подбирают так, чтобы планы получились достаточно точными и лучше использовалось поле чертежа. Масштаб m обычно снабжается индексом, который указывает к какой величине относится этот масштаб.
Размерности масштабов для кинематических величин таковы: масштаба длин – 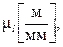 скоростей –
скоростей – 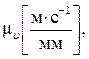 ускорений –
ускорений – 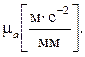 Значение масштаба всегда указывается на чертеже рядом с построением тех величин, для которых он принят.
Значение масштаба всегда указывается на чертеже рядом с построением тех величин, для которых он принят.
Построение планов положения механизма
Планом положения механизма называется графическое изображение взаимного расположения звеньев, соответствующее выбранному моменту времени. Так как во время движения механизма взаимное расположение звеньев всё время меняется, то для того, чтобы наглядно проследить за его движением, строят целый ряд последовательных планов положения механизма. Такое построение особенно удобно по отношению к механизмам с периодическим движением, у которых период равен времени одного оборота кривошипа. Последовательные планы положения механизма соответствуют в точности стробоскопическому эффекту его движения. Для подобных механизмов строят не менее 12 планов положения механизма.
Построение планов положения механизма имеет своей целью:
a) использование его для дальнейших кинематических исследований;
b) предохранение от ошибок при выборе размеров звеньев, так как размеры иногда могут быть выбраны такими, что механизм может заклиниться и не сможет работать;
c) получение габаритов машины, так как можно говорить о габаритах машины только имея взаимное расположение звеньев для целого периода её движения.
Для построения планов положения механизма должны быть заданы:
a) кинематическая схема механизма;
b) размеры звеньев;
c) закон движения ведущего или начального звена.
Метод построения планов положения механизма зависит от степени его сложности, то есть от класса и порядка групп Ассура, входящих в состав механизма. Ниже этот метод рассмотрим применительно к двухповодковым группам первых трёх модификаций, так как подавляющее большинство механизмов состоит из этих групп.
Покажем решение задачи о положениях на конкретном примере.
В качестве примера рассмотрим механизм I – го класса 2 – го порядка, который изображён на рис. 1. Этот механизм называется двухкривошипным шарнирным четырёхзвенником и состоит из группы начального звена OA и одной двухповодковой группы первого вида, состоящей из звеньев 2 – 3. Размеры механизма: lOA = 0.08 м, lBC = 0.1 м, lAB = 0.09 м, lOC = 0.05 м, lBD = 0.06 м. Рассматриваем перманентное движение механизма, при этом ведущее звено движется с постоянной угловой скоростью w1 = 30 с–1. Требуется построить 12 планов положения механизма и шатунную кривую, описываемой точкой M.
Решение.1) Число звеньев механизма k = 4, число подвижных звеньев n = k – 1 = 4 – 1 = 3, число кинематических пар V класса p5 = 4, степень подвижности механизма w = 3n – 2p5 = 3×3 - 2×4 = 1. Формула строения механизма: I(1) ® 2(2,3). В этой формуле римская цифра I обозначает ведущее звено, арабские – класс присоединяемой группы (2), а индексы при арабских цифрах указывают, какие звенья образовали ведущее звено и присоединяемую группу. Из формулы строения механизма видно, что наивысший класс присоединённой группы – второй, поэтому данный механизм при ведущем звене 1 следует отнести ко второму классу.
Построение планов положения механизма ведут в следующем порядке.
a) Наносим на чертеже (рис. 1) неподвижные оси O и C.
b) Размечают положения начального звена. Длину отрезка (OA), изображающего на чертеже размер ведущего звена, принимаем равной 80 мм. Тогда масштаб схемы механизма будет ml = lOA / (OA) = 0.08 / 80 = 0.001 м / мм. Если это звено имеет равномерное вращательное движение и совершает полный оборот, то окружность, которую описывает точка A, делят на 12 (или на 18 или на 24) равных частей. Каждое положение начального звена отмечают определённым номером, и этот номер в дальнейшем относится к плану всего механизма. Например, говорят «план механизма для 2 – го положения».
c) Вычисляем длины отрезков в выбранном масштабе AB, BC, BD, OC: 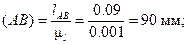
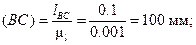
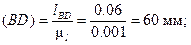
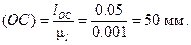
d) Строим положение группы звеньев 2 и 3. После того, как построены планы положения начального звена OA1, OA2, OA3 и так далее, находят соответствующие положения точки B звена 2. Для этого раствором циркуля, равном длине отрезка BC, строят дугу окружности с центром в точке C – траекторию точки B, представляющую собой первое геометрическое место точек, и из точки A1 радиусом A1B проводим окружность, являющуюся вторым геометрическим местом точек B. Положение точки B1 определится на пересечении окружностей.
e) Положение точки D определяем на продолжении линии A1B1.
К построению планов положений механизма
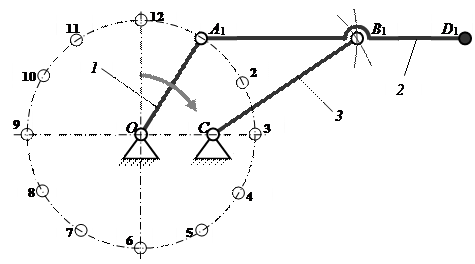 |
Рисунок 1
Положение группы, состоящей из звеньев 2, 3, построено. Строим ряд последовательных положений ведущего звена и группы звеньев 2, 3 на одном и том же чертеже. Обводя последовательные положения точки D плавной кривой, получаем траекторию точки D. Траектории точек звена, не входящего в кинематические пары со стойкой, т.е. шатуна, называются шатунными кривыми.
Шатунными кривыми в настоящее время широко пользуются в технике для воспроизведения движения рабочих органов различных машин и механизмов. Шатунные кривые шарнирного четырёхзвенника общего вида являются алгебраическими кривыми шестого порядка. Шатунные кривые кривошипно-ползунного механизма – алгебраические кривые четвёртого порядка.
Дата добавления: 2015-09-21; просмотров: 1606;
