Лекция 4

Тема: Структурная формула кинематической цепи общего вида. Структурная формула плоских механизмов. Избыточные связи и лишние степени свободы. Структура плоских механизмов.

План лекции.

Структурная формула кинематической цепи общего вида

Если на движение звена в пространстве не наложено никаких условий связи, то оно, как известно, обладает шестью степенями свободы. Тогда, если число звеньев кинематической цепи равно k, то общее число степеней свободы, которым обладают k звеньев до их соединения в кинематические пары, равно 6k. Соединение звеньев в кинематические пары накладывает различное число связей на относительное движение звеньев, зависящее от класса пар. Если число пар I класса, в которые входят звенья рассматриваемой кинематической цепи, равно p₁, число пар II класса – p₂, число пар III класса – p₃, число пар IV класса – p₄ и, наконец, число пар V класса – p₅, то из 6k степеней свободы, которыми обладали звенья до их вхождения в кинематические пары, необходимо исключить те степени свободы, которые отнимаются вхождением звеньев в кинематические пары. Тогда число степеней свободы H, которым обладает кинематическая цепь, равно

H = 6 k – 5 p₅ – 4 p₄ – 3 p₃ – 2 p₂ – p₁. (1)

В конструкциях применяются обычно замкнутые и незамкнутые кинематические цепи, у которых одно из звеньев неподвижно, т.е. является стойкой. Следовательно, при изучении движения всех звеньев кинематической цепи механизма мы рассматриваем их абсолютные перемещения происходящими относительно одного из звеньев, принятого за неподвижное (стойку). Тогда общее число степеней свободы цепи уменьшится на шесть и число степеней свободы W относительно неподвижного звена будет равно

W = H – 6. (2)

Число W степеней свободы кинематической цепи относительно звена, принятого за неподвижное, называется числом степеней свободы кинематической цепи или, кратко, степенью свободы. Подставляя в формулу (2) вместо H его выражение из соотношения (1), получаем

W = 6 (k – 1) – 5 p₅ – 4 p₄ – 3 p₃ – 2 p₂ – p₁. (3)

Если в равенстве (3) обозначить величину k – 1 через n, то получим

W = 6 n – 5 p₅ – 4 p₄ – 3 p₃ – 2 p₂ – p₁, (4)

где n – число подвижных звеньев кинематической цепи. Равенство (4) носит название формулы подвижности или структурной формулы кинематической цепи общего вида. Формула (4) впервые, в несколько ином виде, была дана П.И.Сомовым в 1887 г. и развита А.П.Малышевым в 1923 г. и носит название формулы Сомова – Малышева.

Если кинематическая цепь образована парами только V класса, то формула (4) принимает следующий вид:

W = 6 n – 5 p₅.

Так как механизм представляет собой кинематическую цепь со звеньями, имеющими вполне определённые движения, то необходимо выяснить вопрос о том, как связана определённость движения звеньев механизма с числом его степеней свободы. Как это следует из формулы (4), степень подвижности характеризует число степеней свободы механизма относительно звена, принятого за неподвижное (стойку). Тогда, если механизм обладает одной степенью свободы, то одному из звеньев механизма мы можем предписать относительно стойки какой-либо вполне определённый закон движения (одну обобщённую координату механизма), например, вращательное, поступательное или винтовое движение с заданными скоростями. При этом все остальные звенья механизма получат вполне определённые движения, являющиеся функцией заданного. Если механизм обладает двумя степенями свободы, то необходимо задать одному из звеньев два независимых движения (две обобщённые координаты механизма) относительно стойки или двум звеньям по одному независимому движению относительно стойки и т.д.

Каждая из независимых между собой координат, определяющих положение всех звеньев механизма относительно стойки, называется обобщенной координатой механизма.

Звено, которому приписывается одна или несколько обобщенных координат механизма, называется начальным звеном.

В основном в конструкциях машин и приборов используются механизмы с одной степенью свободы. В некоторых конструкциях машин находят себе применение механизмы с двумя и более степенями свободы. К таким конструкциям относятся дифференциалы автомобилей, некоторые механизмы счётно-решающих машин и манипуляторы.

Структурная формула плоских механизмов

В начале этой лекции было показано, что в общем случае число степенней свободы механизма W может быть определено по структурной формуле (4)

W = 6 n – 5 p₅ – 4 p₄ – 3 p₃ – 2 p₂ – p₁.

Применение этой формулы возможно только в том случае, если на движения звеньев, входящих в состав механизма, не наложено каких-либо общих дополнительных условий. Так, например, можно потребовать, чтобы у механизма, состоящего из одних только вращательных пар V класса, оси всех этих пар были параллельны, пересекались в одной точке и т.д. Оказывается, что такие дополнительные требования существенно изменяют характер движения механизма и изменяют соответственно вид его структурной формулы.

Пусть, например, у механизма, который состоит из кинематических вращательных пар V класса, оси всех пар параллельны (рис. 1). Выберем неподвижную систему координат xyz так, чтобы направление оси x совпало с направлением осей пар, а оси y и z лежали в плоскости, перпендикулярной к осям пар. В этом случае все точки механизма ABCD будут двигаться в плоскостях, параллельных одной общей неподвижной плоскости S, содержащей оси y и z, и мы будем иметь так называемый плоский механизм, т.е. механизм, точки звеньев которого описывают траектории, лежащие в параллельных плоскостях.

Механизм шарнирного четырёхзвенника

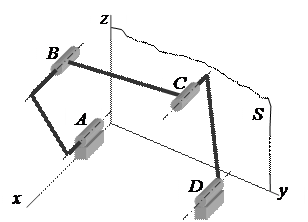Рисунок 1

Рассмотрим, какие общие ограничения наложены на движения всех звеньев этого механизма условием параллельности осей всех кинематических пар. Звенья механизма не могут совершать вращательное движение вокруг осей y и z, поступательное движение вдоль оси x, т.е. из шести возможных движений три не могут быть осуществлены. Следовательно, возможными остаются следующие три движения: вращение вокруг оси x или осей, ей параллельных, и поступательные движения вдоль осей y и z. В самом деле, движение звеньев AB и CD сводится к вращению вокруг осей, параллельных оси x, а движение звена BC как сложное плоскопараллельное движение может быть представлено как вращение вокруг оси, перпендикулярной к плоскости S, и поступательное движение, параллельное этой плоскости.

Если на движение всех звеньев механизма в целом наложено три общих ограничения, то, очевидно, это обстоятельство должно быть учтено при подсчёте числа степеней свободы отдельных звеньев и степеннее свободы механизма в целом. Если в общем случае число степеннее свободы подвижных звеньев механизма равнялось бы 6 n, где n – число подвижных звеньев, то для рассматриваемого механизма число степеней свободы подвижных звеньев будет (6 – 3) n = 3 n. Соответственно вместо 5 p₅ связей, накладываемых парами V класса, в этом механизме пары V класса будут накладывать (5 – 3) p₅ = 2 p₅ связей, так как три связи наложены условием параллельности осей пар, и т.д. Структурная формула механизма (4) будет тогда иной:

W = (6 – 3) n – (5 – 3) p₅ – (4 – 3) p₄ – (3 – 3) p₃,

т.е. степень свободы плоского механизма будет равна

W = 3 n – 2 p₅ – p₄. (5)

Это есть структурная формула для плоских механизмов общего вида.

В состав плоских механизмов пары I, II и III классов входить не могут, как обладающие пространственным характером возможных относительных движений.

Кроме степеней свободы звеньев и связей, активно воздействующих на характер движения механизмов, в некоторых из них могут встретиться степени свободы и условия связи, не оказывающие никакого влияния на характер движения механизма в целом. Удаление из механизмов звеньев и кинематических пар, которым эти степени свободы и условия связи принадлежат, может быть сделано без изменения общего характера движения механизма в целом. Такие степени свободы называются лишними степенями свободы, а связи – избыточными или пассивными связями.

В качестве примера рассмотрим плоский механизм в виде параллелограмма ABCD. Тогда расстояние между точками F и E остаётся постоянным. Тогда звено EF можно удалить без всякого нарушения характера движения механизма, так как оно налагает на движение механизма избыточную связь. Свободно поворачивающийся ролик G даёт лишнюю степень свободы, поэтому его можно удалить.

Схема плоского механизма с пассивными Схема механизма, освобождённого от

связями и лишней степенью свободы пассивных связей и лишней степени свободы

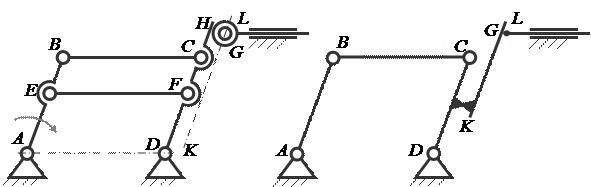
Рисунок 2 Рисунок 3

При исследовании структуры механизма с помощью структурных формул необходимо учитывать возможное присутствие лишних степеней свободы и избыточных условий связи. В дальнейшем при изучении движения звеньев механизмов будем предполагать, что все лишние степени свободы и избыточные условия связи предварительно исключены из механизма удалением соответствующих звеньев, и будем учитывать в механизме только те связи и степени свободы, от которых зависит определённость его движения.

Структура плоских механизмов

Ранее было показано, что структурная формула плоских механизмов (5) в общем случае имеет следующий вид:

W = 3 n – 2 p₅ – p₄.

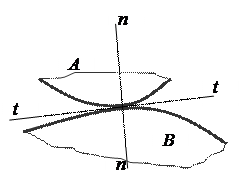
Эта формула впервые выведена российским академиком П.Л.Чебышёвым в 1869 г. Как видно из формулы Чебышёва, плоские механизмы могут быть образованы звеньями, входящими только в кинематические пары IV и V классов. Пары IV класса в плоских механизмах налагают одно условие связи на относительное движение её звеньев. Пары V класса в плоских механизмах налагают два условия связи на относительное движение её звеньев. Рассмотрим некоторые примеры пар IV класса (рис. 4 – 6).

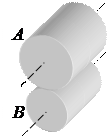
Плоская кинематическая То же из двух криволинейных То же из криволинейного

пара IV класса из двух звеньев звена и звена с остриём

цилиндров

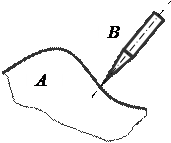Рисунок 4 Рисунок 5 Рисунок 6

Во всех кинематических парах IV класса звенья соприкасаются или в точке. Или по прямой; эти пары относятся к высшим парам.

Пара IV класса в плоском механизме исключает возможность одного какого-либо движения: например, пара, показанная на рис. 5, исключает относительное движение звеньев A и B в направлении нормали n – n к кривым, проведённой в точке их касания перпендикулярно общей касательной t – t. Возможными двумя относительными движениями звеньев этой пары являются качение и скольжение одной кривой по другой. Низшие пары V класса, т.е. пары, в которых касание звеньев происходит по поверхностям в плоских механизмах являются либо вращательными, либо поступательными, так как другие низшие пары, в частности винтовые, не могут входить в состав плоского в силу пространственного характера относительного движения их звеньев. Из трёх возможных относительных движений звеньев пар плоских механизмов вращательные и поступательные пары исключают по два движения. Вращательная пара исключает возможность поступательных движений вдоль двух осей, лежащих в плоскости движения звеньев. Поступательная пара исключает одно поступательное движение и одно вращательное (вокруг оси, перпендикулярной к плоскости движения звеньев).

В зависимости от числа W, стоящего в левой части формулы (5), мы можем получить плоские механизмы с одной, двумя, тремя и т.д. степенями свободы. Так, на рис.7 показан механизм с одной степенью свободы, на рис. 8 – механизм с двумя степенями свободы.

Схема механизма с одной Схема механизма с двумя

обобщённой координатой j₁ обобщёнными координатами j₁ и j₄

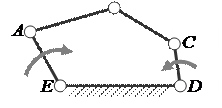
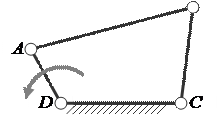
Рисунок 7 Рисунок 8

При нулевой степени свободы кинематической цепи ни одно из звеньев не может двигаться относительно неподвижного звена, и кинематическая цепь превращается в ферму (рис. 9).

Схема кинематической цепи с нулевой степенью свободы

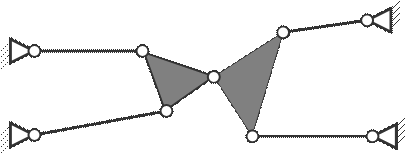Рисунок 9

Для определённости движений всех звеньев механизма, образованного кинематической цепью с одной степенью свободы, необходимо и достаточно иметь заданным закон движения одного из звеньев.

Так для механизма, показанного на рис. 7, достаточно иметь, например, закон движения звена (обозначено дуговой стрелкой) j = f (t) изменения угла j поворота звена в функции времени t, т.е. одну обобщённую координату механизма.

Число W показывает, скольким звеньям необходимо задать законы движения, чтобы получить определённое движение всех остальных звеньев. Обычно в качестве обобщённых координат берутся законы движения звеньев, входящих в кинематические пары со стойками.