Лекция 2. Тема: Основные понятия и определения

Тема: Основные понятия и определения. Кинематические пары. Условия связи. Классификация кинематических пар.

План лекции.

Механизмом называется совокупность связанных между собой тел, имеющих определённые движения. Механизмы служат для передачи или преобразования движения.

Машина(от франц. machine, лат. machine) есть механизм или сочетание механизмов, осуществляющих определённые целесообразные движения для преобразования энергии (энергетические машины), изменения формы, свойств, состояния и положения предмета труда (рабочие машины) или для сбора, переработки и использования информации (информационные машины).

Таким образом, всякая машина состоит из одного или нескольких механизмов, но не всякий механизм является машиной.

Работа механизма или машины обязательно сопровождается тем или иным движением её органов. Это основной фактор, отличающий механизмы и машины от сооружений – мостов, тоннелей, зданий и т.д.

Простейшей частью механизма является звено. Звено – это одно тело или неизменяемое сочетание тел.

Два звена, соединённые между собой и допускающие относительное движение, называются кинематической парой. Кинематические пары бывают низшие и высшие. Звенья низших пар соприкасаются по поверхностям (поступательные, вращательные и винтовые пары), звенья высших пар соприкасаются по линиям и точкам (зубчатые пары, подшипники качения).

Возможные соединения звеньев в кинематические пары весьма разнообразны. Причём, на относительное движение каждого звена накладываются ограничения, зависящие от способа соединения звеньев пары. Эти ограничения назовём условиями связи в кинематических парах.

Как известно, в общем случае всякое свободно движущееся в пространстве абсолютно твёрдое тело (рис. 1), положение которого определяется тремя произвольно выбранными точками A, B и C, обладает шестью степенями свободы. Движение такого тела всегда может быть представлено как вращение вокруг и перемещение вдоль трёх произвольно выбранных взаимно перпендикулярных осей x, y и z. Таким образом, в общем случае, твёрдое тело обладает в пространстве шестью видами независимых возможных движений: тремя вращениями вокруг осей x, y, z и тремя поступательными движениями вдоль тех же осей. Число условий связи может быть только целым и должно быть меньше шести, так как уже в том случае, когда число условий связи равняется шести, звенья теряют относительную подвижность и кинематическая пара переходит в жёсткое соединение двух звеньев. Точно так же число условий связи не может быть меньшим единицы, ибо в этом случае, когда число условий связи равно нулю, звенья не соприкасаются, и, следовательно, кинематическая пара перестаёт существовать; в таком случае мы имеем два тела, движущиеся в пространстве одно независимо от другого.

К определению положения тела в пространстве

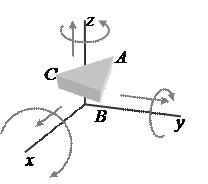Рисунок 1

Итак, число условий связи S, наложенных на относительное движение каждого звена кинематической пары, может располагаться в пределах от 1 до 5, т.е. 1 £ S £ 5. Следовательно, число степеней свободы H звена кинематической пары в относительном движении может быть выражено зависимостью

H = 6 – S . (1)

Из этого равенства следует, что число степеней свободы звена кинематической пары в относительном движении может изменяться также от 1 до 5.

Возможные относительные движения могут быть или независимыми друг от друга, или же быть одно с другим связаны какими-нибудь дополнительными геометрическими условиями, устанавливающими функциональную связь между движениями. Например, в кинематической паре винта и гайки (винтовой паре) вращение винта вокруг оси вызывает его поступательное движение, причём оба эти движения связаны определённой аналитической зависимостью.

Оставшиеся независимыми возможные движения определяют число степеней свободы звеньев кинематической пары в их относительном движении.

Если между простейшими движениями звена вокруг и вдоль трёх координатных осей x, y и z (рис. 1) отсутствуют какие-либо функциональные зависимости, то звено в зависимости от характера связей, налагаемых на его движение относительно другого звена кинематической пары, обладает числом простейших движений от 1 до 5.

Рассмотрим сначала различные кинематические пары, для которых отдельные простейшие возможные движения их звеньев функционально не связаны. Для этих пар числу условий связи, налагаемых на относительное движение их звеньев, соответствует такое же число исключённых простейших возможных движений этих звеньев.

Все кинематические пары делятся на классы в зависимости от числа условий связи, налагаемых ими на относительное движение их звеньев. Так как число условий связи может быть от 1 до 5, то число классов пар равно пяти, в соответствии с чем мы имеем кинематические пары I, II, III, IV и V классов. Класс кинематической пары может быть всегда определён, если будет принята во внимание зависимость (1). Из этого равенства находим

S = 6 – H. (2)

Из равенства (2) следует, что число условий связи S, налагаемых кинематической парой, будет всегда равняться разности между числом шесть и тем числом степеней свободы, которым обладает каждое звено пары в относительном движении. Число условий связи соответствует классу кинематической пары по классификации академика Артоболевского. Рассмотрим несколько примеров.

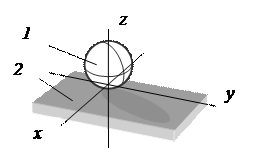Пятиподвижная пара На рис. 2 показана кинематическая пара,

Представляющая собою шар 1, перекаты -

вающийся со скольжением по плоскости 2.

Движение шара относительно плоскости

может быть разложено на три вращения

вокруг осей x, y, z и движение по плоскости 2.

Это движение в свою очередь может быть

разложено на два движения вдоль осей x, y.

Движение шара вдоль вертикальной оси z

Рисунок 2 невозможно, потому что движение ограничено

плоскостью 2, а при движении в обратную

сторону нарушается соприкосновение звеньев, и, следовательно, кинематическая пара перестаёт существовать. Таким образом, движение шара может быть представлено как вращение вокруг трёх осей и движение вдоль двух осей, и число простейших движений, которые может иметь шар, равно пяти. В этом случае число степеней свободы звеньев данной кинематической пары равно пяти и число условий связи равно

S = 6 – H = 6 – 5 = 1.

Поэтому пара, изображённая на рис. 2, должна быть отнесена к парам I класса (пятиподвижная пара).

Примером пары II класса может служить пара, показанная на рис. 3, представляющая собой цилиндр 1, лежащий на плоскости 2. Движение цилиндра 1 относительно плоскости 2, или наоборот, сводится к вращению вокруг осей x и z и скольжению вдоль осей x и y. Таким образом, число простейших движений цилиндра

Четырёхподвижная пара

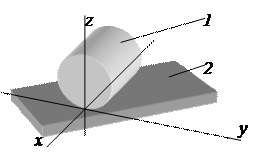
Рисунок 3

равно четырём, т.е. число степеней свободы H звена кинематической равно четырём. Следовательно, число условий связи S равно S = 6 – H = 6 – 4 = 2. Итак, данная кинематическая пара должна быть отнесена к парам II класса (четырёхподвижная пара).

На рис. 4 показан пример пары III класса. Звено 1 заканчивается шаром, входящим в шаровую полость звена 2. Движение звена 1 относительно звена 2, или наоборот, сводится к вращению вокруг осей x, y и z. Следовательно, число степеней свободы H звена кинематической пары равно трём. Число условий связи S равно

S = 6 – H = 6 – 3 = 3,

т.е. пара должна быть отнесена к парам III класса (трёхподвижная пара). Эта пара получила название сферической (шаровой).

Шаровая трёхподвижная пара Цилиндрическая двухподвижная пара

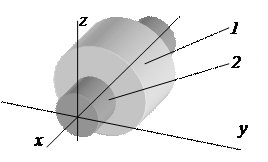
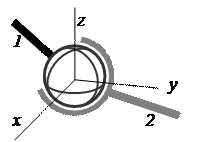
Рисунок 4 Рисунок 5

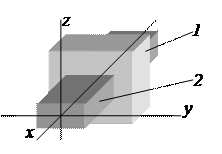
Примером пары IV класса является пара, показанная на рис. 5. Цилиндр 1 находится в полом цилиндре 2. Движение цилиндра 1 относительно цилиндра 2 сводится к вращению и скольжению вокруг и вдоль оси x. Число степеней свободы H равно двум. Следовательно, число условий связи S равно

S = 6 – H = 6 – 2 = 4.

Таким образом, эта пара должна быть отнесена к парам IV класса (двухподвижная пара). Эта пара получила название цилиндрической пары.

На рис. 6 показан пример пары V класса. В этой паре соединение звеньев 1 и 2 образуется двумя цилиндрами, находящимися в постоянном соприкосновении. Бурты внутреннего цилиндра препятствуют движению одного цилиндра относительно другого в направлении оси x – x, но не препятствуют вращению одного из них относительно другого. Поэтому число степеней свободы H этой пары равняется единице, и, следовательно, число условий связи в этой кинематической паре

S = 6 – H = 6 – 1 = 5.

Вращательная пара Поступательная пара

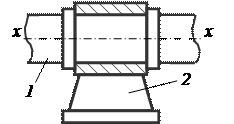Рисунок 6 Рисунок 7

Таким образом, эта пара должна быть отнесена к парам V класса (одноподвижная пара). Эта пара получила название вращательной пары.

На рис. 7 показана кинематическая пара V класса, каждое из звеньев которой обладает только одним возможным простейшим движением, а именно, поступательным движением вдоль оси x.

Поэтому число степеней свободы H этой пары равняется единице, и, следовательно, число условий связи S в этой кинематической паре равно

S = 6 – H = 6 – 1 = 5.

Таким образом, эта пара должна быть отнесена к парам V класса (одноподвижная пара). Эта пара получила название поступательной пары.

Итак, кинематические пары в зависимости от числа условий связи, налагаемых на относительное движение их звеньев, могут быть разделены на пять классов.

Рассмотренные выше кинематические пары относились к парам, для которых мгновенные возможные движения их звеньев не зависят друг от друга. Однако в технике встречаются кинематические пары, для которых относительные движения их звеньев связаны какой-либо дополнительной геометрической зависимостью. Рассмотрим вид такой пары, наиболее часто встречающейся в механизмах. На рис. 8 показана одна пара IV

Винтовая пара

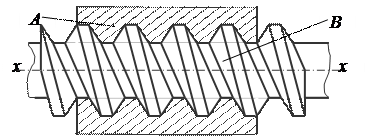
Рисунок 8

класса, относительные движения звеньев которой связаны условием, что заданному углу j поворота одного звена относительно другого вокруг оси x – x соответствует поступательное перемещение h вдоль той же оси. В этом случае, хотя звенья пары имеют и поступательное, и вращательное движения, эти движения связаны условием

h = f(j) (3)

и, таким образом, на относительное движение звеньев пары наложена ещё одна дополнительная связь, выраженная соотношением (3). В этом случае пара должна быть отнесена не к IV, а уже к V классу. Подобные пары весьма часто встречаются в технике и носят название винтовой пары из-за винтового характера относительного движения их звеньев. Для того чтобы элементы кинематических пар находились в постоянном соприкосновении, они должны быть замкнуты. Замыкание может быть либо геометрическим, либо силовым.

Геометрическое замыкание осуществляется соответствующими геометрическими формами элементов звеньев кинематической пары. Например, все пары, изображённые на рис. 4 – 8, являются замкнутыми геометрически, потому что касание элементов звеньев этих пар обеспечивается их геометрическими формами.

Чтобы пары, показанные на рис. 2 – 3, были замкнутыми, необходимо шар и цилиндр прижимать к плоскости какой-нибудь силой. Силовое замыкание осуществляется силой веса, силой упругости пружин и т.п.